Часть 8. Практикум
П1. Задания по теме "Математический анализ, функции одной переменной"
Найти множества значений x, удовлетворяющих следующим условиям.
2. Найти пределы.
3. Найти области определения функций.
4. Найти пределы.
5. Найти точки разрыва следующих функций и определить их тип.
6. Найти производные функций.
7. Составить уравнения касательных к графикам функций.
8. Найти производные высших порядков от следующих функций.
А) Производные второго порядка
Б) Производные третьего порядка
В) Производные n-го порядка
9. Найти пределы с использованием
А) правила Лопиталя:
Б) разложения по формуле Маклорена:
10. Исследовать и построить графики функций.
11. Найти неопределенные интегралы
а) непосредственным интегрированием:
б) методом подстановки:
в) интегрированием по частям:
12. Решить задачи с определенными интегралами.
1) Вычислить интегралы.
2) Найти площади фигур, ограниченных следующими линиями.
12.29. Фигура ограничена параболой у = x2 + 4x — 3 и касательными к ней в точках а (0, -3), b(3, 0).
12.30. Фигура ограничена параболой у = x2 — 2x + 2, касательной к ней в точке (3, 5) и осью Оу.
3) Найти объемы тел, образованных вращением вокруг оси Оу фигуры, ограниченной следующими линиями.
4) Вычислить несобственные интегралы.
П2. Задания по теме "Математический анализ, функции нескольких переменных"
1. Найти области определения следующих функций.
2. Построить линии уровня следующих функций.
3. Найти частные производные от функций.
4. Найти градиенты функций в следующих точках.
5. Найти частные производные второго порядка от функций.
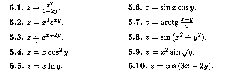
6. Найти экстремумы функций.
П3. Задания по теме "Обыкновенные дифференциальные уравнения"
1. Найти общие решения уравнений первого порядка методом разделения переменных.
2. Найти частные решения уравнений первого порядка, удовлетворяющие следующим начальным условиям.
3. Найти общие решения линейных уравнений первого порядка.
4. Решить уравнения Бернулли.
5. Найти решения линейных однородных уравнений второго порядка.
6. Решить линейные неоднородные уравнения второго порядка.
7. Найти частные решения линейных уравнений второго порядка, удовлетворяющие указанным начальным и краевым условиям.
П4. Задания по теме "Элементы линейной алгебры"
1. Вычислить
где , и — векторы, заданные в таблице.
Найти следующие комбинации этих матриц.
2.1. Матрицу H = 3С - 4F.
2.2. Соответствующие транспонированные матрицы.
2.3. Все возможные произведения матриц, имеющие смысл.
2.4. Матрицу Н = С2 - F2.
2.5. Матрицу Н = G3.
3. Вычислить определители:
4. Определить, являются ли векторы а, b и с линейно независимыми. Варианты задания этих векторов указаны в таблице задания 1.
5. Найти ранги матриц, указанных в задании 2.
6. Решить методом Крамера системы линейных уравнений.
7. Решить задачи 6.1-6.6 методом обратной матрицы, вычислив ее методом Гаусса.
8. Решить методом Гаусса системы линейных уравнений 6.3-6.6.
9. Решить методом Гаусса системы линейных уравнений.
10. Найти фундаментальные системы решений систем однородных уравнений.
11. Найти собственные значения и собственные векторы матриц.
П5. Задания по теме "Элементы теории вероятностей"
1. Задачи на случайные события
1.1. Два нумизмата обмениваются коллекционными монетами. Найти число способов обмена, если первый нумизмат обменивает 5 монет, а второй — 8 монет.
1.2. В ящике находится 12 деталей, среди которых имеются 3 нестандартные. Найти вероятность того, что 3 взятые наугад детали будут стандартными.
1.3. В урне находится 20 шаров: 15 белых и 5 красных. Из урны извлекают один шар, затем, не возвращая его обратно, извлекают второй. Найти вероятность появления красного шара при втором извлечении.
1.4. Абонент забыл последнюю цифру телефонного номера. Найти вероятность того, что при наборе номера наугад он наберет его правильно не более чем с четырех попыток.
1.5. В лотерее разыгрывается 150 вещевых и 50 денежных выигрышей на каждые 5000 билетов. Найти вероятность выигрыша вообще.
1.6. В ящике находится 12 деталей, из которых 3 нестандартные. Из ящика последовательно, одну за другой, берут две детали. Найти вероятность того, что обе детали будут стандартными.
1.7. В цеху находятся четыре однотипных станка. Вероятности исправного состояния этих станков соответственно равны 0,7, 0,9, 0,8 и 0,6. Найти вероятность того, что все станки находятся в эксплуатации.
1.8. На станции «Скорой помощи» дежурят две машины. Вероятности технической исправности машин равны соответственно 0,95 и 0,75. Найти вероятность исполнения поступившего вызова второй машиной.
1.9. Инвестиционный фонд вкладывает поровну средства в пять предприятий при условии возврата ему каждым предприятием через определенный срок 125% от вложенной суммы. Вероятность банкротства каждого из предприятий равна 0,3. Найти вероятность того, что по истечении срока кредита фонд получит обратно не менее вложенной суммы.
1.10. Таможенный досмотр автомашин осуществляют два инспектора. В среднем из каждых 100 машин 45 проходит через первого инспектора. Вероятность того, что при досмотре машина, соответствующая таможенным правилам, не будет задержана, составляет 0,95 у первого инспектора и 0,85 у второго. Машина, соответствующая таможенным правилам, не была задержана. Найти вероятность того, что она прошла досмотр у первого инспектора.
1.11. В первой коробке находится 10 шаров, из которых 4 синих; во второй коробке — 5 шаров, из которых 3 синих. Из первой коробки наугад перекладывают один шар во вторую коробку. Найти вероятность извлечения из второй коробки синего шара.
1.12. Три орудия произвели залп по цели, и два снаряда поразили ее. Найти вероятность поражения цели при залпе вторым орудием, если вероятности поражения цели орудиями равны соответственно 0,5, 0,6 и 0,7.
1.13. Найти вероятность поражения цели при залповой стрельбе отделением из 5 солдат, если вероятность попадания в цель каждым солдатом составляет 0,5.
1.14. Из урны, содержащей белые и черные шары, извлекают по одному шару 4 раза. Найти вероятность появления белого шара: а) менее трех раз; б) не менее трех раз.
1.15. Вероятность выпуска стандартного изделия равна 0,9. Найти вероятность того, что среди 100 приобретенных изделий будет ровно 80 стандартных.
1.16. Вероятность обращения в банк клиента за возвратом депозита равна 0,3. Найти вероятность того, что из 100 клиентов, посетивших банк, ровно 30 потребуют возврата депозита.
1.17. Вероятность появления брака в каждом из 2500 изделий равна 0,2. Найти вероятность появления стандартных изделий в количестве: а) не менее 1250; б) не менее 1200 и не более 1250; в) не более 1249. Выпуск каждого изделия полагать независимым событием.
1.18. Вероятность обращения в травматологический пункт для каждого рабочего на стройке составляет 0,3. Найти, среди какого количества строителей следует ожидать обращения в пункт не менее 50 человек.
1.19. Банк выдал кредиты размером 400 тыс. р. каждому из 2000 клиентов на год под 15% годовых. Вероятность невозврата кредита каждым из клиентов составляет 0,05. Какой доход гарантирован банку с вероятностью: а) 0,7; б) 0,95 ?
1.20. Вероятность появления события в каждом из 1200 независимых испытаний равна 0,6. Найти вероятность отклонения относительной частоты появления события от его вероятности не более чем на 2% по абсолютной величине.