Дроби 107

Значение чисел и отношения между ними также играют немалую роль в платоновской философии130. Как Платон использо­ вал их для описания философских или нравственных проблем, мы обсудим в параграфе 3.1.

2.7. Дроби

Мало что зная об учении о рациональных числах, «мы можем толь­ ко с уверенностью утверждать, что такое учение существовало»1 . Ясно лишь то, что чистая математика во времена Платона допускала

существование только целых чисел, а дроби в качестве чисел не

132

рассматривались . Вместо дробей греки использовали отношения между целыми числами. Это менее удобно, но при этом впечатляет, «с какой удивительной строгостью, общностью и глубоким пони­ манием существа проблемы была построена древними первая тео­ рия пар и введен закон композиции для этих новых объектов»

О смысле и значении чисел в платоновской философии см.: Radke. Die Theorie der Zahl im Piatonismus. На с 430 мы читаем: «"Необычное" для нас представление о "числе" — необычное в том отношении, что оно обшир­ нее, чем наше стандартное представление, ограничивающееся количест­ венным и абстрактно вычислительным свойствами и далекое от того, чтобы обладать функцей учреждения своих принципов, — которое обосно­ вывается в платонизме, может стать понятнее через анализ обычно используемых нами понятий. Ведь в итоге он покажет, что знакомые нам понятия о "числе" вовсе не могут мыслиться как нечто определенное, без того чтобы предполагалось это определенное первоначальное понятие числа и учреждающие его понятия. В ходе такого анализа становится ясно, почему в сущности необходимо, наряду с абстрактными понятиями о числах, с помощью которых мы считаем, предположить кроме того (необычное для нас) всеобъемлющее понятие числа».

История математики с древнейших времен до начала XIX столетия. С. 70.

Подробное изложение см. в работе: Fowler. The Mathematics of Plato's Aca­ demy. P. 222-276. Фаулер утверждает, что «у нас нет никаких надежных свидетельств того, что греки использовали обыкновенные дроби или имели представление о них» (Р. 263).

История математики с древнейших времен до начала XIX столетия. С. 72.

108СУЩНОСТЬ МАТЕМАТИКИ И ЕЕ ФУНКЦИИ

Вчастности, Платон объяснял, почему единицу следует брать только как целое. Это важно не только из-за ее главенствующего положения в пифагорейской мистической нумерологии, но и по следующей причине: при делении единицы мы получаем несколько частей, т. е. множество, большее единицы, что является бес­ смысленным:

Ты ведь знаешь, что те, кто силен в этой науке, осмеют и отвергнут попытку мысленно разделить самое единицу, но если ты все-таки ее раздробишь, они снова умножат части,

боясь, как бы единица оказалась не единицей, а многими

134

долями одного Греческим математикам было, конечно же, известно, что

торговые агенты и архитекторы использовали дроби без каких-либо проблем135, но сами они не хотели задействовать столь «низкий» инструмент. Ван дер Варден пишет об этом так: «До Архимеда дроби вообще не входили в официальную греческую науку. Но это объясняется не тем, что их не знали, а скорее тем, что их не хотели знать... Дробями пренебрегали и предоставляли их купцам...» Мордухай-Болтовской поддерживает это мнение, ссылаясь на

134 Государство. 525е. Здесь можно привести слова Юлиуса Штенцеля, который, ссылаясь на мнение Генриха Шольца, писал: «В то время, как для профана b = 3Аа, для серьезного математика это выглядит, как 5Ь = За. Шольц, ссылаясь на схолию к диалогу «Хармид»... делает вывод... что древние греки знали исчисление в дробях, например египетское, но намеренно "оставляли за дверью" все арифметические действия, связанные с дробями. Пропорция (logos) делает для греческой арифметики дробь ненужной, в то время как для египтян дробь явилась... новым типом числа, который они использовали наряду с целым числом» (Stenzel. Zahl und Gestalt bei Platon und Aristoteles. S. 148. Примеч. 2).

Уже древние египетские математики использовали дроби и умели их складывать, вычитать, умножать и делить, правда, только на «эмпири­ ческом» уровне. Вавилонские математики также использовали дроби в своей шестидесятеричной системе. См. удивительные примеры в книге: Раик. Очерки по истории математики в древности. С. 5-146.

Ван дер Варден. Пробуждающаяся наука. С. 68-69.

Дроби 109

определение 3 в книге VII «Начал» Евклида: «Часть есть число в числе, меньшее в большем, если оно измеряет большее». Он ком­

ментирует это определение следующим образом: «В подлиннике

137

καταμετρή — "измеряет", но ни в коем случае не "делит"» Штенцель, однако, не был столь категоричен: «Если поставить вопрос, разработали ли греки методы исчисления с дробями, то факты свидетельствуют против однозначного ответа, положитель­ ного или отрицательного». Он указывает на определение 4 в VII книге Евклида: «Части же, если оно его не измеряет...», где

множественное число слова «части» означает такие дроби, как 23,

138

34, 45 и т. д. В общем, Штенцель говорит об «особенном отношении к дробям»1 у греков, но при этом он согласен, что дроби не находились в центре внимания, так как пропорции сделали «разрушение» единицы ненужным. И действительно, чаще всего вместо дробей математики пользовались пропорциями, в которых были задействованы только целые числа

Добавим к сказанному слова Фаулера на этот счет: древние греки не использовали дроби, так как «они не думали о соот­ ношениях, подобных нашим рациональным числам, и потому не

Примечание Мордухай-Болтовского (Евклид. Начала. Кн. VII-X. С. 9). Stenzel. Zahl und Gestalt bei Platon und Aristoteles. S. 28.

Ibid. S. 33. M. Выгодский также констатирует, «что греки имели не один, а целых три способа канонического представления дробей. Один из них — это наш способ образования "обыкновенных" дробей. Ему соответствует в греческом языке способ словесного выражения, вполне аналогичный существующему в русском языке: мы выражаем, например, дробь 7/60 словами "семь шестидесятых" (частей)... Точно так же образуется соответствующее греческое название той же дроби επτά έξέκοσται (μέρη). Письменное выражение обыкновенных дробей совершалось у древних греков различными способами» (Выгодский. Арифметика и алгебра в древнем мире. С. 276).

Античная арифметика не имела способа описания всех соотношений вели­ чин, конструируемых в геометрии. Для решения этой проблемы Евдокс создает довольно глубоко разработанную теорию пропорций, которая сохранилась в книге V «Начал» Евклида.

Иррациональные отношения 111

Фаулер оспаривал достоверность таких рассказов; по его дан­ ным, древние источники никогда не упоминают о каком-то изумле­ нии такого рода. Аристотель, например, часто критиковал пифаго­ рейскую философию, но не говорил, что несоизмеримость разру­ шает ее главную догму «Все есть число». Теэтет (147d-148b) «не дает никаких указаний на то, что явление несоизмеримости представляло какую-то фундаментальную концептуальную трудность для математиков; скорее оно рассматривается в качестве источника интересных и плодотворных проблем» . А. Е. Раик также констатирует, что «доказательство этого факта, т. е. иррациональности V2, принадлежащее пифагорейцам, не вызывало никаких сомнений» (курсив наш. — В. 3.). Невообразимой была для них только мысль о том, что соотношению несоизмеримых отрезков мог бы соответствовать новый вид чисел, — то, что мы называем сегодня «иррациональными числами», например л/2146

144Fowler. The Mathematics of Plato's Academy. P. 290.

145Раик. Очерки по истории математики в древности. С. 157.

146Иррациональное, кстати, является «невообразимым» не только для древ­ них греков, но и для некоторых современных математиков. Уже Кеплер напоминал о том, что стороны семиугольника являются иррациональными, и делал такой вывод: «Это важный факт. В этом лежит причина того, что Бог не использовал семиугольники для украшения мира, как он сделал это с простыми фигурами» (Kepler. Weltharmonik. S. 45). И математик Л. Кронекер сказал однажды: «Господь сотворил целые числа; остальное

— дело рук человека» (цит. по. Bell: Die grossen Mathematiker. S. 453).

Кроме того, согласно Расселу, привычные обоснования для существования иррациональных чисел стоят на «глиняных ногах»: «Уравнение х2 - 2 = 0,

как утверждалось, должно иметь решение, поскольку с ростом JC от 0 до 2, х2 - 2 увеличивается и, являясь сначала отрицательным, затем становится

положительным; если χ изменяется непрерывно, то же происходит с JC - 2; следовательно, х2 - 2 должен стать равным 0 при переходе от отрицатель­ ного значения к положительному. Или, опять же, было отмечено, что

диагональ квадрата со стороной равной 1 имеет, очевидно, точную и определенную длину *, и что эта длина такова, что х2 - 2 = 0. Но такие аргументы были не в силах доказать, что χ действительно является числом. Они могут в равной степени рассматриваться как демонстрации неадек­ ватности чисел алгебре и геометрии» (Rüssel. The Principles of Mathematics.

112 СУЩНОСТЬ МАТЕМАТИКИ И ЕЕ ФУНКЦИИ

Все же проблема иррациональных отношений играет важней­ шую роль в развитии древнегреческой математики. Согласно иссле­ дованиям Ван дер Вардена, это открытие привело к изложению алгебры полностью в геометрической форме (в конце этого парагра­ фа мы приведем пример подобной геометрической конструкции). Как подчеркивает Ван дер Варден, это было естественным шагом для греческих математиков в силу логической строгости их взглядов: «Мы в настоящее время говорим, что длина диагонали выражается "иррациональным числом" V2, и чувствуем свое превосходство над бедными греками, которые "не знали, что такое иррациональные числа". Однако греки знали очень хорошо иррациональные отношения. Как мы увидим далее, они имели очень ясное представление об отношении диагонали к стороне квадрата и были в состоянии совершенно безукоризненно доказать, что это отношение не может быть выражено в целых числах. И если они не рассматривали V2 как число, то это было результатом не их неведения, но только того, что они строго держались своего опре­ деления числа. "Arithmos" обозначает количество, а следовательно, и целое число. Логическая строгость не позволяла им допускать даже дробей, и они заменяли их отношением целых чисел. — Для вавилонян же каждый отрезок и каждая площадь представляли собой просто-напросто число. Они даже и не задумывались, когда приходилось площадь прямоугольника сложить с его основанием. Когда они не могли точно извлечь квадратный корень, то спокойно удовлетворялись приближением. Инженеры и естествоиспытатели во все времена поступали точно так же. Но для греков имело

Р. 282). Знаменитое «Дедекиндово сечение» тоже не дает никаких доказа­ тельств существования иррациональных чисел; «Таким образом, существо­ вание иррациональных чисел не доказано, они могут быть просто удобной выдумкой» (Ibid.). То же самое необходимо сказать и о теории Вейерштрасса: «Ряды рациональных чисел не могут доказать существование иррациональных чисел как своего предела, а только могут доказать, что, если существует такой предел, он должно быть иррациональным» (Ibid. Р. 268; см. целиком главу XXXIV «Infinity and Continuity», где Рассел обсуждает все проблемы обоснования иррациональных чисел).

Иррациональные отношения 113

значение точное знание, "диагональ в самой своей сущности", как выражает это Платон, а не допустимое приближенное значение. — Уравнение χ =2 не может быть разрешено ни в области целых чисел, ни даже в области отношений чисел. Но оно вполне разрешимо в области прямолинейных отрезков: действительно, его решением является диагональ квадрата со стороной, равной единице. Следовательно, для того чтобы получить точное решение квадратного уравнения, нам надлежит из области чисел перейти в область геометрических величин. Геометрическая алгебра приложима также и к иррациональным отрезкам и тем не менее является точной наукой. Следовательно, не только наслаждение зримым, но и логическая необходимость заставила пифагорейцев преобразовать их алгебру в геометрическую форму»

Интересно посмотреть, как греки доказывали несоизмеримость стороны квадрата и его диагонали. В приложении к книге X «Начал» Евклида мы находим старинное доказательство, которое, несомненно, было известно уже Платону. Оно построено на косвенном способе доказательства148 и опирается на некоторые свойства четных и нечетных чисел. Как мы уже говорили, в своих диалогах Платон неоднократно рассуждал о четных и нечетных числах. Рассматриваемое старинное доказательство достаточно сложно149, поэтому понятно, почему факт несоизмеримости долгое время оставался неизвестным.

Ван дер Варден. Пробуждающаяся наука. С. 175.

Подобный метод вызывает какое-то неудобство или даже сомнение — мы еще скажем об этом в параграфе 3.11.

Греческая система цифр (цифры записывались буквами α, β, γ'...) была не слишком удобна, поэтому греки предпочитали математические рассуж­ дения в геометрической форме. Сегодня в нашем распоряжении есть средства (арабские цифры, алгебраические знаки), делающие доказатель­ ства намного короче и нагляднее. Теорему несоизмеримости стороны квадрата и его диагонали в наше время можно доказать следующем образом: возьмем квадрат ABCD с диагональю А С и предположим, что АС линейно соизмерима с AB. Допустим, отношение АС : AB в численном выражении равно m : я, где тип — натуральные, взаимно простые числа

114 СУЩНОСТЬ МАТЕМАТИКИ И ЕЕ ФУНКЦИИ

Приведем доказательство несоизмеримости стороны квадрата и его диаметра из «Начал» (X):

Пусть нам будет предложено доказать, что для квадратных фигур диаметр будет линейно несоизмерим со стороной.

Пусть квадрат будет ABCD, диаметр же его АС; я утверждаю, что CA будет линейно несоизмерима с AB.

квадрата на AB (предложение 47 книги I). И поскольку CA соизмерима с AB, то, значит, CA имеет к AB отношение как число к числу (предложение 6). Пусть оно будут иметь то, которое El имеет к Я, и пусть ΕΙ, Я будут наименьшие из имеющих с ними одно и то же отношение (ср. предложение 33 книги VII); значит, El не будет единицей. Действительно, если El будет единицей, имеет же к Я отношение, какое АС имеет к AB, и АС больше AB, то, значит, и El (единица) больше Я — числа (предложение 14 книги V);

(т. е. m и η имеют только один общий делитель, равный единице). Из АС : AB = m : η следует (AC)2 : (AB)2 = m2 : η2. Согласно теореме Пифагора, мы знаем, что (АС)2 = 2(АВ)2, следовательно, 2 = т2: п2 или т2 = 2л2, значит, т2

— четное число и, следовательно, само m — четное число (это заключение верно, так как квадрат нечетного числа тоже нечетен!) Так как m — четное число, существует число h = т/2. Отсюда, m = 2h. Следовательно, т2 = ЛИ2. Поскольку выше мы получили т2 = 2п , то 2п2 = Ah2, следовательно, п2 = 2л2. Значит, η — четное число и, следовательно, η — тоже четное число. Но по условию тип взаимно простые числа, и если т, как мы видели выше, четное число, то η должно быть нечетным. Это противоречие, и значит, что наше первоначальное предположение, что диагональ квадрата АС линейно соизмерима со стороной квадрата AB, неверно. Отсюда следует, что диагональ квадрата линейно несоизмерима с его стороной, что и требовалось доказать.

150«Понятие диаметра было обычным у Евклида и других авторов для обозначения диаметра квадрата, а также параллелограмма; диагональ была более поздним термином, введенным Героном» (Heath. The Thirteen Books of Euclid's Elements. Vol. 1. P. 185).

Иррациональные отношения 115

это же нелепо. Значит, El единицей не будет; значит, будет числом. И посколько будет, что как прямая CA к AB, так и число El к Я, то, значит, и как квадрат на CA к квадрату на AB, так и квадрат на El к квадрату на Я (предложение 20 книги VI, следствие; предложение 11 книги VIII). Квадрат же на CA вдвое больше квадрата на AB, значит, и квадрат на El вдвое больше квадрата на Я; значит, квадрат на El будет четным; так что и само El будет четным. Действительно, если бы оно было нечетным, то и квадрат на нем был бы нечетным, поскольку ведь, если складываются сколько угодно нечетных чисел и количество же их нечетно, то и целое будет нечетным (предложение 23 книги IX); значит, El будет четным. Разделим его пополам в G. И поскольку El, Я суть наименьшие из имеющих с ними то же отношение, то они будут первыми между собой (предложение 21 книги VII). И El четное; значит, Я будет нечетным. Действительно, если бы оно было четным, то числа El, Я измеряла бы двойка; ибо всякое четное число имеет половинную часть (определение 6 книги VII); между тем, они являются первыми между собой; это же невозможно. Четным, значит, не будет Я; значит — нечетным. И поскольку El вдвое больше EG, то, значит, квадрат на El в четыре раза больше квадрата на EG (предложение 11 книги VIII). Квадрат же на El вдвое больше квадрата на EG; значит, и квадрат на Я вдвое больше квадрата на EG; значит, четным будет квадрат на Я Четным, значит, вследствие вышесказанного, будет и Я; но оно же и нечетное; это же невозможно. Значит, CA не будет линейно соизмеримым с AB; что и требовалось доказать.

Факт несоизмеримости стороны квадрата и его диагонали (а также несоизмеримости некоторых других отрезков в геометрии), т. е. факт существования «иррациональных соотношений», был известен Платону1 \ который, согласно исследованиям Фаулера,

См., напр.: Гиппий Больший. ЗОЗЬ — «Что же мешает, чтобы... две величины, каждая из которых неопределенна, взятые вместе, давали бы то определенную, то неопределенную величину?..» Э. Хайч в комментарии к этому отрывку отмечает, что утверждение Сократа, «что сумма двух иррациональных слагаемых может быть иногда рациональной, иногда ир­ рациональной, часто вообще не рассматривается некоторыми исследо-

Иррациональные отношения 117

вали длиной, а всякий отрезок, который дает разностороннее продолговатое число, мы назвали [несоизмеримой с единицей] стороной квадрата, потому что такие отрезки соизмеримы первым не по длине, а лишь по площадям, которые они образуют. То же и для объемных тел153.

В «Филебе» (16с-18с) Платон приводит замечательные рассуж­ дения, тесно связанные с проблемой существования чисел, которые не могут быть записаны полностью. Они, по мнению Платона, содержат некоторую «опасность»:

Беспредельное множество отдельных вещей и [свойств], содержащихся в них, неизбежно делает также беспредельной и бессмысленной твою мысль, лишает ее числа, вследствие чего ты никогда ни в чем не обращаешь внимания ни на какое число

Одна из проблем, например, состоит в том, что ряд натуральных чисел, начиная с единицы155, содержит в себе, с одной стороны, конечное, ограниченное множество, но, с другой — множество беспредельное, ничем не ограниченное. Оба «конца» совпадают друг с другом диалектически, как «сросшиеся воедино предел и беспредельность» 6. Но оказывается, что между единством и

Теэтет. 148а. Ср. со словами Евы Сакс: «Платон знает и цитирует в "Государстве" (VII, 534d) и "Теэтете" (148а) учение Теэтета об άλογοι γραμμαί. Но, согласно Евклиду (Def. X 1,4), άλογος — это прямая, квадрат которой не рационален; этот факт показывает, что Платон знал и другие геометрические площади (έτερα τίνα ευθύγραμμα), которые были нерацио­ нальны» (Sachs. Die fünf platonischen Körper. S. 172).

Филеб. 17e.

Таково и наше представление. Для греков первым числом было «три» — см. подробное описание в работе: Гайденко. Обоснование научного знания в философии Платона. С. 102-118.

Филеб. 16с. Об этом совпадении в примеч. 26 к диалогу «Парменид» пишет А. Тахо-Годи: «Идея единства этих двух, как будто бы столь различных, категорий бытия всегда была близка античности» (Платон. Собр. соч. в 4-х томах. Т. 2. С. 509).

118 СУЩНОСТЬ МАТЕМАТИКИ И ЕЕ ФУНКЦИИ

беспредельным имеется что-то еще, то, что должно, по мнению Платона, обязательно исследоваться и упорядочиваться:

Теперешние мудрецы устанавливают единство как придется

— то раньше, то позже, чем следует, и сразу после единства помещают беспредельное; промежуточное же от них ускользает157.

Платон прямо не поясняет, что же это такое — «промежу­ точное», которое легко ускользает от нашего внимания. Вот что он говорит по этому поводу в «Филебе»:

Все, о чем говорится как о вечно сущем, состоит из единства и множества и заключает в себе сросшиеся воедино предел и беспредельность. Если все это так устроено, то мы всякий раз должны вести исследование, полагая одну идею для всего, и эту идею мы там найдем. Когда же мы ее схватим, нужно смотреть, нет ли кроме одной еще двух, а может быть, трех идей или какого-то иного их числа, и затем с каждым из этих единств поступать таким же образом до тех пор, пока первоначальное единство не предстанет взору не просто как единое, многое и беспредельное, но как количественно определенное. Идею же беспредельного можно прилагать ко множеству лишь после того, как будет охвачено взором все его число, заключенное между беспредельным и одним; только тогда каждому единству из всего [ряда] можно дозволить войти в беспредельное и раствориться в нем. Так вот каким образом боги, сказал я, завещали нам исследовать все вещи, изучать их и поучать друг друга158.

В диалоге «Парменид» мы также находим рассуждения, показы­ вающие, что у Платона были некоторые догадки о том, что сущест­ вуют не только «единица» и «бесконечное» как экстремальные

Филеб. 1 бе-17а. Филеб. 16с-е.

Иррациональные отношения 119

пункты, но и целый мир разных множеств . Поэтому Платон ставит задачу привести в порядок хаос беспредельного, т. е. определить иррациональность конструктивно160 и классифицировать ее161. В

Ср., напр.: Парменид. 158с—d — «Итак, если постоянно рассматривать таким образом иную природу идеи саму по себе, то, сколько бы ни сосредоточивать на ней внимание, она всегда окажется количественно беспредельной. — Безусловно, так. — С другой же стороны, части, поскольку каждая из них стала частью, обладают уже пределом как друг по отношению к другу, так и по отношению к целому и целое обладает пределом по отношению к частям. — Несомненно. — Итак, другое в отношении единого, как оказывается, таково, что если сочетать его с единым, то в нем возникает нечто иное, что и создает им предел в отношении друг друга, тогда как природа другого сама по себе — беспредельность». О рассуждениях Феодора («Теэтет») о различных нерациональных отношениях см. также параграф 2.9 наст. изд.

Примером простой, наглядной конструкции, известной древним матема­ тикам, является Золотое сечение. Оно делит непрерывную величину S на две части в таком отношении, при котором меньшая часть Т2 так относится к большей Г/, как большая Г/ ко всей величине 5, то есть Tj : S = Т2 : Tj. Если мы возьмем Tj как новую величину, а Т2 как большую и Т3 как меньшую части, то Золотое сечение выглядит так: Т2 : Tj = Т3 : Т2 , и следовательно, мы получим Т3 : Т2 = Т2 : Г/ = Tj : 5, то есть, если продолжить процесс тем же способом, то значение дробей Тп+] : Тп неизменно соответствует иррациональному числу 1,6180339887... в совре­ менных обозначениях.

Древние греки рассматривали иррациональные соотношения только геоме­ трически. Они не считали «дроби» числами, и тем более не могли представить, что существуют иррациональные числа. «Диагональ квадрата несоизмерима с его стороной» — это они доказали, но не выражали отношение «диагональ : сторона» числом, как делаем это мы с помощью знака «V2». Поэтому о том, что мы назвали «занялись классификацией иррациональности в геометрии», правильней было бы сказать: «занялись классификацией разных степеней несоизмеримости в геометрии». То, что древние греки уже начали это классифицирование, подчеркивает О. Беккер: они в какой-то степени различали ступени и виды формирования иррациональных отношений в том смысле, что формулировки этих отно­ шений становились все более сложными и «не до конца произносимыми» (Becker. Mathematische Existenz. S. 578). X книга «Начал» Евклида в осо­ бенной степени показывает стремление конструировать и классифициро­ вать иррациональное. Такая классификация имела ценность для Платона

120 СУЩНОСТЬ МАТЕМАТИКИ И ЕЕ ФУНКЦИИ

соответствии с этим требованием греческие математики, прежде всего Теэтет и Евдокс, занялись классификацией иррациональности в геометрии162, правда ограничиваясь конструкциями, которые могли быть построены с помощью «идеальных» циркуля и линейки (см. параграф 2.3).

Добавим несколько слов о геометрической форме математики, чтобы получить какое-то представление о том, как во времена Платона греки — да и сам Платон — ею занимались. Их геометрическое воображение было поразительным, но у них не было наших алгебраических возможностей. Кольман пишет об этом так: «Открытие несоизмеримости, невозможность выразить отно­ шение любых двух целых чисел привели к тому, что греки стали употреблять не арифметические, а геометрические отношения для выражения общих отношений между величинами. У них создалась своеобразная "геометрическая алгебра". Именно по этой причине, а вовсе не из-за особого предрасположения "греческого духа" к

потому, что «она выявляет способ бытия этих величин в градации, в кото­ рой они шаг за шагом удаляются от рациональных пропорций, которые можно выразить понятными грекам числами (αριθμοί)» (Ibid. S. 576).

См. короткое изложение у Кольмана: «Ученик Теодора из Кирены, Теэтет Афинский (около 414-369 гг. до н. э.) внес два важных вклада в математику, вошедшие позже в "Начала" Евклида. Во-первых, он дал классификацию иррациональностей. Кроме отрезков, соизмеримых и несоизмеримых Уд, вводится так называемая медиаль (в нашем обозначении -J^Tfb , где а и Ъ — соизмеримы), далее биномиаль Vä+Vfr ,

Вторая гексада иррациональности отличается от первой тем, что упомянутое только что произведение иррационально. Третья и четвертая гексады аналогичны предыдущим двум, отличаясь от них лишь тем, что место сложения занимает вычитание; величина вида -Ja--JE (в нашем написании) называется вычет» (Кольман. История математики в древ­ ности. С. 112). Подробное изложение см. в работе: Раик. Очерки по исто­ рии математики в древности. С. 157-165.

Иррациональные отношения 121

геометрическим формам, как это утверждают идеалисты, у греков геометрия стала играть роль алгебры»163. Этот геометрический путь «был ошибкой в стратегии, хотя на первых порах античная мате­ матика получила большие тактические преимущества. Построение алгебры на основе геометрии впервые позволило обосновывать общим образом некоторые теоремы и правила алгебры, однако при дальнейшем развитии геометрическое облачение как панцирь сковало живое тело античной математики. Оно мешало гармо­ ничному развитию отдельных частей математики, делало ее громоздкой и малоподвижной. Геометрическая броня античной математики походила на внешний скелет панцирных животных, который при дальнейшей эволюции был заменен внутренним скелетом»1 . Чтобы читатель мог «прочувствовать» особенности геометрического метода, применявшегося Платоном и древними греческими математиками, приведем несколько примеров.

Чтобы продемонстрировать для начала преимущество reo-

метрического метода, возьмем формулу (а + Ь) = а + lab + Ъ , которая непонятна для многих школьников. В геометрической форме это уравнение сразу становится очевидным: большой квадрат

Кольман. История математики в древности. С. 116.

164История математики с древнейших времен до начала XIX столетия. Т. I. С. 78.

Иррациональные отношения 123

на половину окружности) точка С касания перпендикуляра с кругом определяет угол прямоугольного треугольника. Его высота равна Vô, так как по теореме о высоте прямоугольного треугольника произведение частей гипотенузы, на которые их делит высота, — 1 и Ь — равно квадрату высоты: \ b = (Vè)2.

μ

Второй шаг: нарисуем отрезок AB = а. Проведем перпендикуляр m через середину отрезка. От точки касания С отложим отрезок равный Vb, конец этого отрезка - точка О. Нарисуем окружность с центром О и радиусом а/2. Определим точки касания окружности с отрезком AB : D и Ε. Тогда отрезок DB является одним решением дг/, и отрезок ЕВ другим решением Х2 уравнения χ - ах + Ъ = 0.

oc=V£

126 СУЩНОСТЬ МАТЕМАТИКИ И ЕЕ ФУНКЦИИ

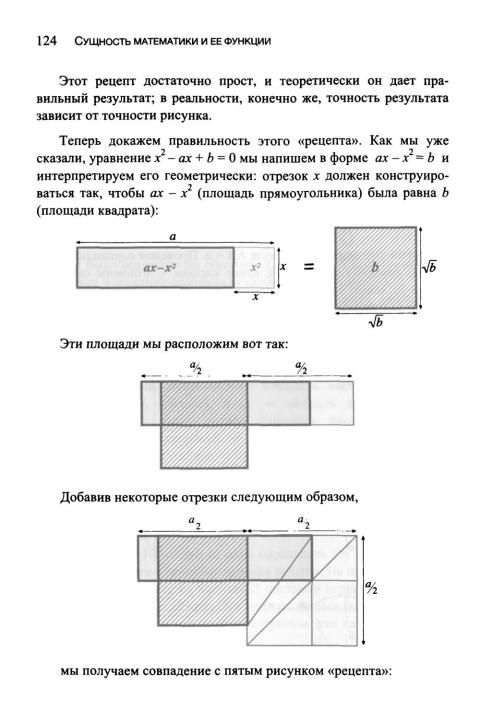
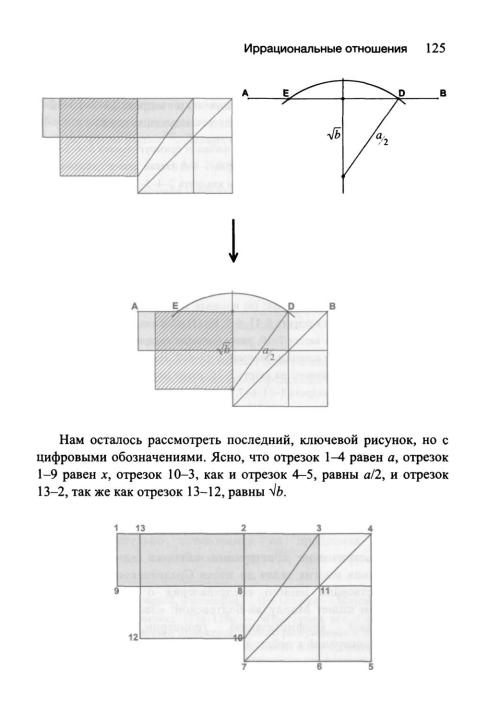
Теперь наша задача такова: доказать равенство площадей прямо­ угольника 1-3-11-9 (его площадь равна ах-х ) и квадрата 13-2-10-12 (его площадь равна Ь). Для этого проделаем следующие шаги:

(1) Площадь прямоугольника 1-2-8-9 равна площади прямоугольника 3-4-5-6. Из этого следует: (2) площадь фигуры 1-3-6-7-8-9 (такая «многоугольная» фигура называется «гномон») равна площади квадрата 2-4-5-7. Далее: из того, что отрезок 10-3, как и отрезок 4-5, равен я/2, следует: (3) площадь квадрата под отрезком 10-3 равна площади квадрата 2-4-5-7. Из (2) и (3) следует: (4) площадь квадрата под отрезком 10-3 равна площади гномона 1-3-6-7-8-9. Теперь рассмотрим прямоугольный треугольник 2-3-10. Согласно теореме Пифагора, получается: (5) площадь квадрата, построенного на катете 2-10, равна квадрату, построенному на гипотенузе 10-3, минус площадь квадрата, построенного на катете 2-3. Дальше: (6) площадь квадрата, построенного на катете 2-3, равна площади квадрата 8-11-6-7. Из (5) и (6) следует: (7) площадь квадрата, построенного на катете 2-10, равна площади квадрата, построенного на гипотенузе 10-3, минус площадь квадрата 8-11-6-7. Из (7) и (4) следует (8) площадь квадрата, построенного на катете 2-10, равна площади гномона 1-3- 6-7-8-9 минус площадь квадрата 8-11-6-7. Но гномон 1-3-6-7-8-9 минус ква­ драт 8-11-6-7 — это прямоугольник 1-3-11-9. Поэтому: (8') площадь квадра­ та, построенного на катете 2-10, равна площади прямоугольника 1-3-11-9. А в нашей конструкции мы выбрали отрезок 1-4 равный я, и отрезок 2-10 равный

А если мы обозначаем отрезок 3-4 величиной х, мы получаем для площади прямоугольника 1-3-11-9 выражение (α-χ)·χ, и для площади квадрата 13—2— 10-12 выражение (^Ь)2 = Ъ. А мы доказали геометрически, что площади прямоугольника 1-3-11-9 и квадрата 13-2-10-12 равны, поэтому получается алгебраическое уравнение (а - х) · χ = b, или χ - αχ + b = 0.

Такие геометрические конструкции являлись единственным способом решения многих задач до эпохи Средневековья, так как еще не существовало нашего представления о вещественных числах. Об этом пишет Мордухай-Болтовской: «Заслугой Декарта иногда считают арифметизацию геометрии, приведение геометрических операций к действиям над числами. Но это неверно. Это было бы возможно только в том случае, если бы Декарт представлял себе взаимно-однозначное соответствие между