§2. Капиллярные явления. Формула Жюрена

Капиллярные явления наблюдаются, когда жидкость проникает в трубки с очень узкими каналами (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капилляре зависит от того, смачивает или не смачивает жидкость его стенки, точнее, от значения краевого угла смачивания.

Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается (рис.30).

В первом капилляре (см. рис.30, а) поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа (давление направлено к центру кривизны) поднимает её в капилляре. Кривизна поверхности жидкости во втором капилляре (см. рис.30, б) положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой H:

(XII.3)

где  – плотность жидкости; ₀ ^– плотность газовой фазы; g – ускорение свободного падения; r – радиус мениска.

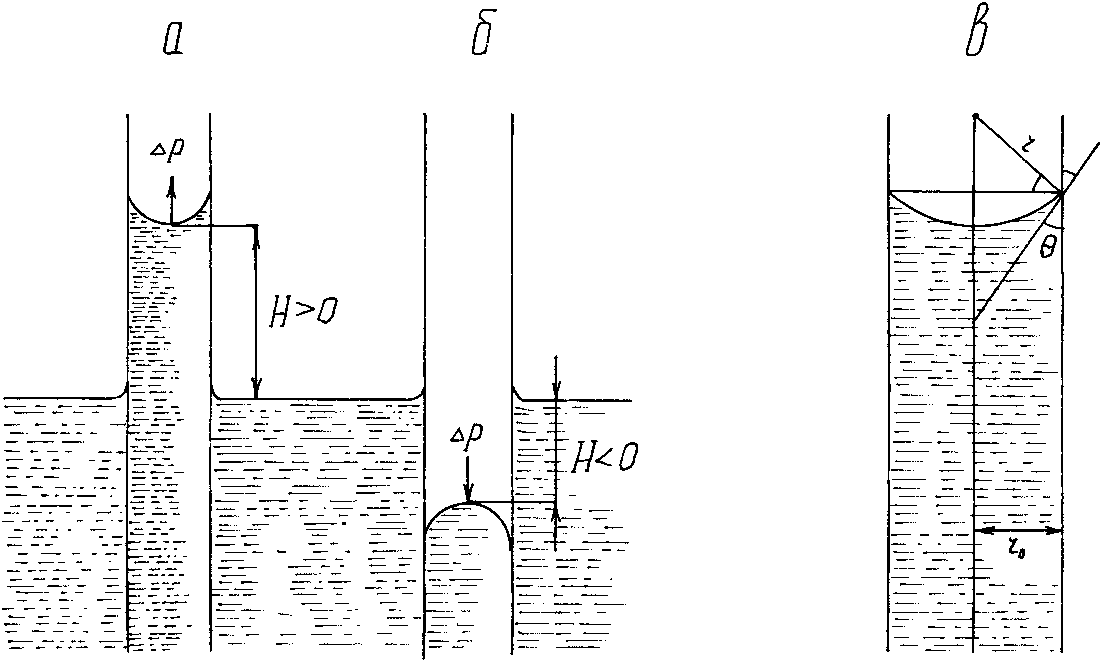
Рис.30. Капиллярное поднятие жидкости:

a – cos  > 0: б – cos  < 0: в – связь радиуса кривизны мениска r с радиусом капилляра r₀.

Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания  и радиус капилляра r₀. На рис.30, в показан (в увеличенном виде) мениск жидкости в капилляре. Видно, что

r₀ = rcos, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:

(XII.4)

При отсутствии смачивания  > 90°, cos  < 0, уровень жидкости в капилляре опускается на величину H. При полном смачивании  = 0, cos  = 1, в этом случае радиус мениска равен радиусу капилляра.

Краевой угол для воды и низших углеводородов на стенке стеклянного капилляра мал. Для большинства других жидкостей он меньше 10°. Расчет по уравнению (XII.4) показывает, что относительная погрешность, обусловленная приравниванием этого угла в стеклянном капилляре нулю, не превышает 1,5%. Измерение высоты капиллярного поднятия лежит в основе одного из наиболее точных методов определения поверхностного натяжения жидкостей.

Капиллярным поднятием жидкостей объясняется ряд известных явлений и процессов: пропитка бумаги и тканей обусловлена капиллярным поднятием жидкости в порах; водонепроницаемость тканей обеспечивается их гидрофобностью и как следствие – отрицательным капиллярным поднятием; подъем воды из почвы по стволам деревьев происходит благодаря волокнистому строению древесины и т. д.

§3. Роль капиллярных явлений при вытеснении нефти водой из пористых сред

Поровое пространство нефтесодержащих пород представляет собой огромное скопление капиллярных каналов, в которых движутся несмешивающиеся жидкости, образующие мениски на границе раздела фаз. Этим обстоятельством обусловлено существенное влияние капиллярных явлений на процессы вытеснения нефти.

Если порода гидрофильна, то в области водонефтяного контакта давление, развиваемое менисками, способствует процессам капиллярного впитывания и перераспределения жидкостей.

Кроме того, капиллярные силы влияют на процессы диспергирования и коалесценции (слияния) частиц нефти и воды в пористой среде.

Интенсивность упомянутых капиллярных процессов зависит в той или иной степени от величины капиллярного давления.

Изменяя качества нагнетаемых в залежь вод, можно воздействовать на их поверхностное натяжение на границе с нефтью, смачивающие характеристики, а также вязкостные свойства. Это означает, что изменяя упомянутые свойства, мы прежде всего влияем на комплексный параметр – капиллярные свойства пластовой системы, т. е. на значение и знак капиллярного давления.

В гидрофобных пластах, где возникает противодействие вытеснению нефти водой, капиллярные силы вредны. Лучший результат можно получить, если нефть вытесняется водным раствором с низким значением межфазного натяжения.

Роль капиллярных сил в гидрофильных породах заключается в использовании эффекта впитывания воды в нефтенасыщенные блоки для существенного увеличения извлечения нефти из трещиновато-пористых коллекторов.

Считается, что во всех случаях водные растворы, развивающие в пористой среде высокое капиллярное давление, более предпочтительны для заводнения нефтяных залежей.

Благоприятное влияние капиллярных процессов в зоне водонефтяного контакта на нефтеотдачу неоднородного пласта выражено в гораздо меньшей степени.

Изучение процессов вытеснения нефти водой с учетом капиллярных процессов и капиллярных характеристик пластовых систем позволяет определить влияние на нефтеотдачу как условий вытеснения, так и физико-химических свойств пластовых жидкостей и пород.

ПРЕДМЕТ ФИЗИЧЕСКОЙ ХИМИИ

Физическая химия занимается рассмотрением главным образом двух групп вопросов:

1. Изучением свойств и строения различных веществ в зависимости от их химического состава, химического строения и от условий существования;

2. Изучением химических реакций и других форм взаимодействия между веществами или частицами в зависимости от их химического состава, строения, условий, в которых происходит процесс, а также от внешних воздействий (электрических, световых и др.).

Содержание курса физической химии обычно делят на несколько основных разделов, характеризующих направление этой науки и определяющих ее предмет.

Строение вещества. В этот раздел входит учение о строении атомов и молекул и учение об агрегатных состояниях вещества. Учение о строении атомов в курсе физической химии необходимо для выяснения вопросов образования молекул из атомов, природы химической связи, внутренней структуры молекул.

В учении об агрегатных состояниях рассматривается зависимость строения и важнейших свойств веществ, находящихся в газообразном, кристаллическом и жидком состояниях, от их состава.

Химическая термодинамика. В этом разделе физической химии рассматриваются основные соотношения, вытекающие из первого закона термодинамики. Они позволяют рассчитать количество выделяемой или поглощаемой теплоты химического процесса и определить, как будет влиять на него изменения внешних условий.

На основе второго закона термодинамики определяется возможность самопроизвольного течения процесса в интересующем нас направлении, а так же условия и положение равновесия и его смещения под влиянием изменения внешних условий.

Учение о растворах рассматривает природу растворов, их внутреннюю структуру и важнейшие свойства, зависимость свойств растворов от концентрации и химической природы компонентов и вопросы растворимости.

Электрохимия изучает некоторые особенности свойств растворов электролитов, электропроводность растворов, процесса электролиза, работу ГЭ и электрохимическую коррозию металлов.

Химическая кинетика изучает скорость и молекулярный механизм химических реакций как в гомогенной, так и в гетерогенной среде, включая и явления катализа.

Учение о коллоидном состоянии веществ и поверхностных явлениях – самостоятельный раздел.

ТЕМА 1

ФАЗОВЫЕ РАВНОВЕСИЯ. ФИЗИКО-ХИМИЧЕСКИЙ АНАЛИЗ.

1. Общие понятия. Правило фаз.

Фазовыми равновесиями называются равновесия, которые устанавливаются между отдельными фазами при физических процессах перехода веществ из одной фазы в другую. К числу таких переходов относятся плавление и кристаллизация индивидуальных веществ, кристаллизация веществ из растворов, испарение и сублимация, конденсация газообразных веществ, аллотропические превращения веществ, превращения ферромагнетика в парамагнетик и др.

Фазовые равновесия определяются соотношением термодинамических параметров (концентрация, t , Р, напряженность магнитного поля, напряженность электрического поля) и описываются уравнением Клаузиуса – Клайперона и формулой Дж.Гиббса 1876 г.

С = К – Ф + n (1.1)

Эта формула получила название правила фаз. Она связывает число термодинамических степеней свободы, число независимых компонентов и число фаз системы.

Фазой называется однородная часть системы, обладающая одинаковыми интенсивными свойствами и отделенная от других частей системы поверхностью раздела.

Например, система из насыщенного раствора NaCl и монокристалла NaCl состоит из двух фаз. Если вместо монокристалла в системе будет порошок кристалликов NaCl, то все эти кристаллики вместе составят одну фазу, т.к. они представляют собой совокупность частей системы, одинаковых по всем интенсивным свойствам.

При фазовых переходах происходит выравнивание химических потенциалов. Например, если химический потенциал компонента в растворе выше, чем его химический потенциал в паре, то будет происходить испарение этого компонента из жидкого раствора, пока химические потенциалы не сравняются. В результате пар станет насыщенным, и в системе установится равновесие.

Число фаз в системе будем обозначать символом Ф.

Числом независимых компонентов К называется наименьшее число индивидуальных веществ в системе, достаточное для образования всех фаз данной системы. Их этого определения следует, что понятие «независимый компонент» не тождественно с понятием «индивидуальное вещество». Число независимых компонентов может совпадать и не совпадать с числом индивидуальных веществ.

Например, в трехфазной системе С₆ Н ₁₂ О₆ (к) кристаллы сахара + насыщенный водный раствор + водяной пар имеется два индивидуальных вещества - вода и сахар и два независимых компонента 1 фаза - сахар, вторая - сахар + вода, третья - вода.

В системе, состоящей из трех индивидуальных веществ СаО, СаСО₃ , СО₂ число независимых компонентов равно не трем а только двум (безразлично каким именно).

Выберем в качестве независимых компонентов СаО и СО₂ , тогда первая фаза образована СаО, вторая СаО и СО₂ , которые в результате реакции дают СаСО₃ , третья фаза - СО₂ .

Система, состоящая из NH₄Cl в смеси с NH₃ + HCl в эквимолярных количествах, состоит из трех индивидуальных веществ, но только из одного независимого компонента - NH₄Cl , достаточного для образования всех фаз данной системы (твердой фазы NH₄Cl и газообразной, получаемой термическим разложением NH₄Cl NH₃ + HCl)

Т.о. число независимых компонентов К равно числу индивидуальных веществ минус число уравнений, связывающих эти вещества.

В примере первом К = 2 - 0 = 2 , во втором К = 3 – 1 = 2 , К = 3 – 2 = 1 в третьем (здесь вторым уравнение является условие [NH₃] =[HCl]).

Число степеней свободы определяется как число условий ( t ,­­ Р, концентрация), которые можно произвольно менять ( в известных пределах), не изменяя числа или вида фаз системы.

Сумма числа степеней свободы системы и числа фаз ее равна сумме независимых компонентов и числу внешних факторов, влияющих на равновесие этой системы:

С + Ф = К + n (1.2)

Если на систему воздействуют два фактора t , Р , то правило фаз запишется в виде

С = К – Ф + 2 (1.3)

Число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только температура и давление, равно числу независимых компонентов системы минус число фаз плюс два.

Правило фаз показывает, что число степеней свободы возрастает с увеличением числа компонентов и уменьшается с увеличением числа фаз системы.

Число степеней свободы не может быть отрицательным, поэтому правило фаз нередко выражают так же следующим соотношением:

Ф <= К + 2 (1.4)

Число степеней свободы определяется как вариантность системы. По этому признаку - числу степеней свободы, системы разделяют на инвариантные или безвариантные ( при С = 0) , моновариантные или одновариантные (при С = 1 ), дивариантные или двухвариантные (при С = 2)… Поливариантными или многовариантными, называются системы с большим числом степеней свободы.

2. Однокомпонентные системы

При К = 1 соотношение (1.3.) принимает вид: С = З – Ф. Т.к. число степеней свободы не может быть отрицательным, то в этом случае число фаз находящихся между собой в равновесии, не м.б. больше трех и , следовательно, здесь можно иметь только три типа систем: однофазные, двухфазные и трехфазные.

Для однофазных систем С = 2 , для двухфазных С = 1 и для трехфазных С=0.

Диаграмма, выражающая зависимость состояния системы (и фазовых равновесий в ней) от внешних условий или от состава системы, называется диаграммой состояния или фазовой диаграммой.

Такие диаграммы строятся по соответствующим опытным данным и широко применяются для характеристики различных систем.

1. Диаграмма состояния воды

Рис. 1.1. Диаграмма состояния воды в области невысоких давлений.

ОД - продолжение кривой ОС.

Она определяет давление насыщенного пара над переохлажденной водой. Такое состояние неустойчиво и переохлажденная вода всегда обладает большим Р_пара, чем лед при тех же условиях.

Кривая ОС представляет зависимость давления насыщенного пара жидкой воды от t.

ОА - зависимость давления насыщенного пара от t.

ОВ - зависимость температур замерзания воды от внешнего давления.

Эти три кривые разделяют диаграмму на поля, каждое из которых отвечает одному из агрегатных состояний - пару, жидкости, льду.

Сами кривые отвечают равновесию между соответствующими двумя фазами:

ОС - жидкость-пар

ОА - лед-пар

ОВ - лед-жидкость

Точка О характеризует условия равновесия одновременно между всеми тремя фазами - паром, льдом и жидкой водой.

Сами кривые отвечают равновесию между соответствующими двумя фазами.

Однофазные состояния воды обладают двумя степенями свободы. В этом случае мы можем изменять в определенных пределах как t , так и Р (поля диаграммы) каждое независимо от изменений другого, что не вызывает изменения числа или вида фаз системы.

Двухфазные состояния воды представляются линиями, которые ограничивают соответствующие поля диаграммы. Число степеней свободы в этих случаях уменьшается до единицы (одновариантные системы). Не изменяя числа или вида фаз, можно изменять только t или Р. При этом с изменением одного из этих параметров другой тоже не сохраняет прежнего значения, а изменяется в соответствии с изменением первого.

Точка О, называемая тройной точкой, отвечает равновесию одновременно между всеми тремя фазами. Число степеней свободы в этом случае равно нулю (система безвариантна). Существует только одно сочетание t и Р, при котором рассматриваемые три фазы могут находится в равновесии.

2. Диаграмма состояния серы.

Сера может существовать в виде двух твердых модификаций - ромбической S_(ромб) и моноклинной S_(мон) , жидкости S_(ж) и газа S_{(г)­ .}

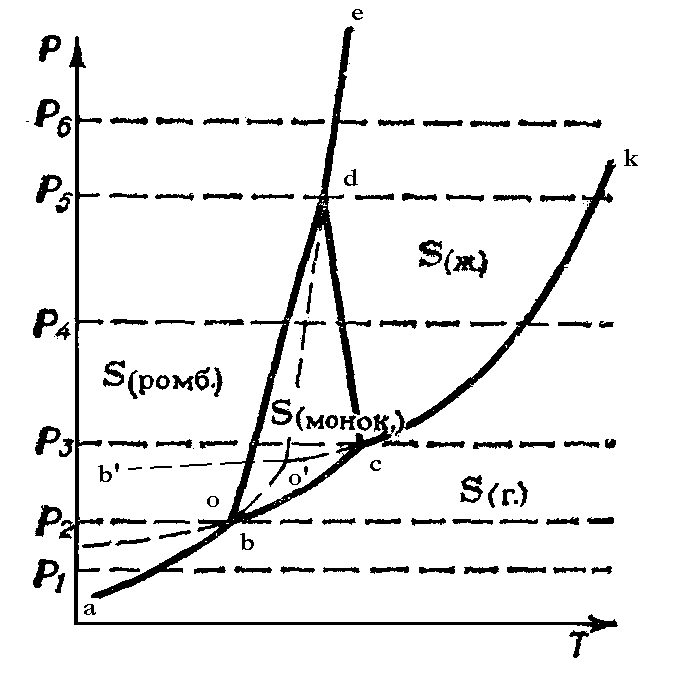
Сплошные линии аb, bс, сk, bd, сd и dе изображают на диаграмме устойчивые двухфазные равновесия:

S_(ромб) S_(г)­ линия ab

S_(мон) S_(г)­ линия bc

S_(ж) S_(г)­ линия ck

S_(ромб) S_(мон) линия bd

S_(мон) S_(ж) линия cd

S_(ромб) S_(ж) линия de

Рис. 1.2. Диаграмма состояния серы.

Точки b, d, c являются тройными точками, которые изображают состояния устойчивых равновесий в трехфазной системе:

т. b Т=368,65 k, Р=0,496 Па

S_(ромб) S_(мон) S_(г)

т.с Т=392,45 k, Р=3,346 Па

S_(мон) S_(ж) S_(г)

т.d Т=424,15 k, Р=1,305 х 10⁸ Па

S_(ромб) S_(мон) S_(ж)

Пунктирные линии bO, cO и dO соответствуют на диаграмме метастабильным двухфазным равновесиям:

bO - S_{(ромб)(перегр).} S_(г) [пересыщенная относительно S_(мон) ];

cO - S_{(ж)(переохл).} S_(г) [пересыщенная относительно S_(мон) ];

dO - S_{(ромб)(перегр).} S_(ж) [переохлажденная]

Линии bc, bd, cd и линии bO, cO, dO ограничивают области однофазной бивариантной системы:

Область bOd - перегретой S_(ромб)

Область cOd - переохлажденной жидкой серы

область bOc - газообразной серы, пересыщенной относительно S_(мон)

Точка О является тройной точкой и изображает на диаграмме неустойчивое метастабильное трехфазное равновесие:

S_{(ромб)(перегр.)} S_{(ж)(переохл.)} S_{(г)(пересыщенная относительно} S_(мон)

Жидкую серу можно переохладить до t более низкой, чем t метастабильной трехфазной системы (точка О). На диаграмме это изображено - ОО’ , которой соответствует двухфазному метастабильному равновесию:

S_{(ж)(переохл.)} S_{(г)(пересыщенная относительно.} S_{(мон) и} S_(ромб))

Линия bb’ изображает двухфазное метастабильное равновесие:

S_{(мон)(переохл.)} S_{(г)(пересыщенная относительно} S_(ромб))

3. Двухкомпонентные системы.

Двухкомпонентными системами являются сплавы двух различных металлов, солей, минералы, любой раствор, состоящий из растворителя и одного растворенного вещества.

По правилу фаз Гиббса в 2-х компонентной системе равновесие возможно при

Число фаз	Правило фаз Гиббса С=К-Ф+2
1	С=2-1+2=3
2	С=2-2+2=2
3	С=2-3+2=1
4	С=2-4+2=0

Из анализа 2-х компонентных систем по правилу фаз следуют такие заключения:

1. Наибольшее число фаз, находящихся в равновесии в 2-х компонентной системе равно 4. Это две твердые фазы I и II компонента, жидкая фаза и пар.

2. Наибольшее число степеней свободы в 2-х компонентой системе равно 3 - это t, Р и концентрация одного из компонентов С.

Концентрация другого компонента величина зависимая и описывается уравнением:

С₂ = 100% - С₁

Т.о. полная диаграмма состояния 2-х компонентной системы должна строиться по трем пространственным осям - t, Р и состав.

В большинстве случаев 2-х компонентные системы являются сконденсированными, т.е. состоят из жидкости и твердого вещества.

Величина давления пара не влияет на их равновесие и поэтому не учитывается. Правило фаз упрощается

С = К – Ф + 1

Диаграмма состояния конденсированных 2-х компонентных систем может быть построена на плоскости t- состав. Она называется диаграммой плавкости.

Это график зависимости t плавления (отвердения) каждого из компонентов от их концентрации в системе. Диаграмму плавкости строят на кривых охлаждения или нагревания. Они представляют зависимость t 2-х компонентных систем определенного состава от времени при их равномерном охлаждении или нагревании.

Условия равновесия и состав фаз конденсированных 2-х компонентных систем зависят от характера взаимодействия.

1. 2-х компонентные системы без химического взаимодействия.

1. Неизоморфные конденсированные системы.

Системы с неограниченной растворимостью компонентов в жидком и взаимной нерастворимостью в твердом состоянии.

Кривые 1, 2, 3, 4 характеризуют охлаждение сплавов обоих компонентов с избытком одного из них. В начале t жидкого сплава равномерно снижается. При некоторой t скорость охлаждения замедляется и наклон кривой становится меньше. Это объясняется тем, что в сплаве появляются кристаллики избыточного компонента и выделяющаяся при этом теплота кристаллизации частично компенсирует теплоту плавления.

По мере выделения кристаллов вещества сплав обедняется им и поэтому t кристаллизации снижается. Наконец, при определенной t состав жидкой фазы сплава становится таким, что оба вещества кристаллизуются одновременно. Температура при этом остается постоянной пока сплав не отвердеет полностью. После этого начинается равномерное охлаждение твердого сплава.

Кристаллизация сплавов начинается при разных t в зависимости от исходного содержания каждого компонента. Окончательное отвердение происходит при одной и той же температуре.

Минимальная t , при которой начинается плавление 2-хкомпонентной системы (или заканчивается кристаллизация расплава), называется ЭВТЕКТИЧЕСКОЙ температурой Т_э .