§ 3. Реальные растворы. Положительные и отрицательные отклонения от закона Рауля

Закон Рауля не выполняется для реальных растворов. Парциальные давления этих растворов больше или меньше давлений паров идеальных растворов. Отклонения от закона Рауля в первом случае называются положительными (общее давление пара больше аддитивной величины), а во втором случае – отрицательными (общее давление пара меньше аддитивной величины).

Примерами растворов с положительными отклонениями от законов Рауля могут служить растворы:

ацетон – этиловый спирт

бензол – ацетон

вода – метиловый спирт

На рис.6 изображена диаграмма P – х для одного из этих растворов (бензол – ацетон).

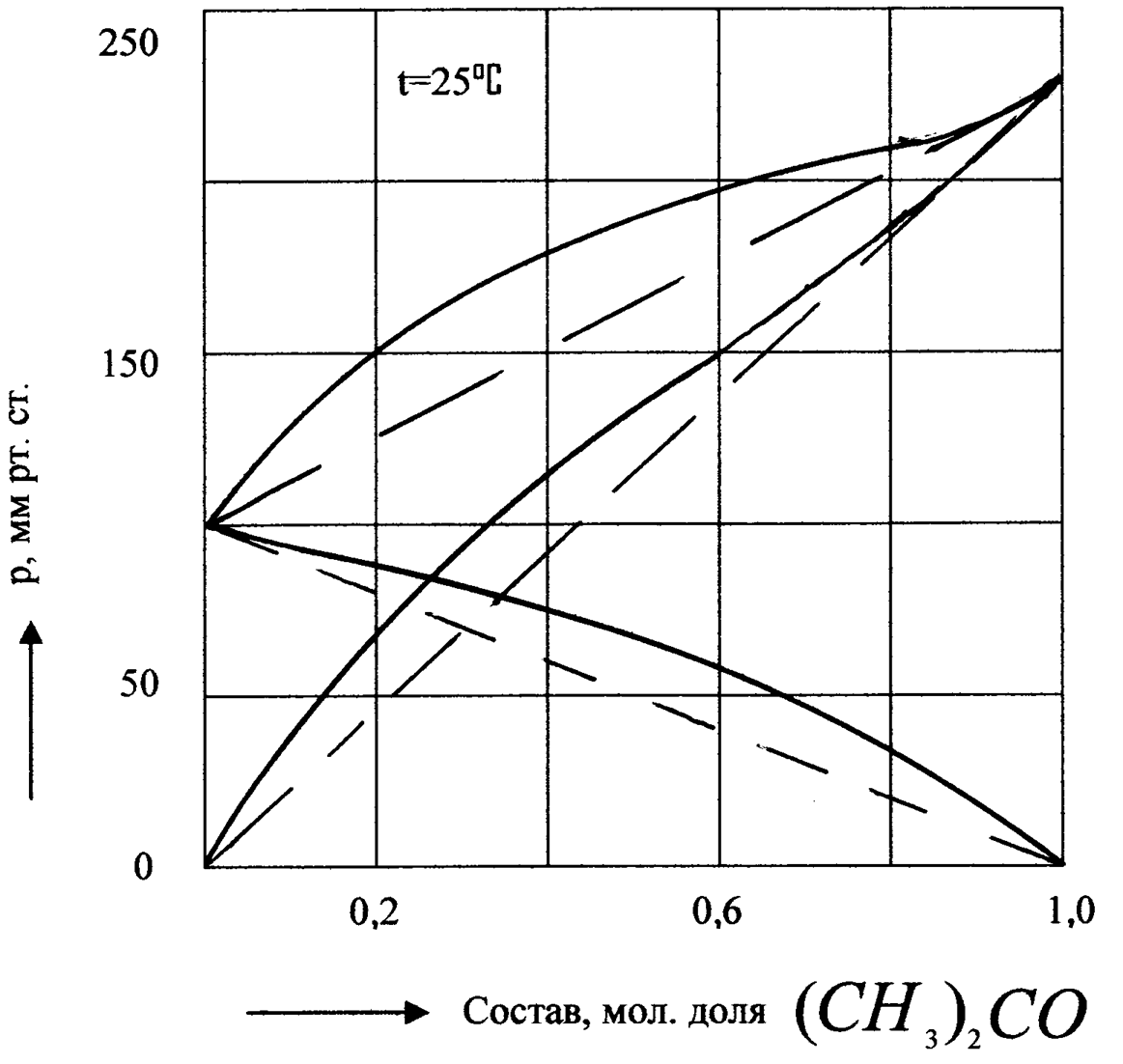
Рис.6. Диаграмма давления пара над раствором С₆Н₆ – (СН₃)₂СО.

К растворам с отрицательными отклонениями от законов Рауля относятся, например, растворы:

хлороформ – бензол

хлороформ – диэтиловый эфир

Диаграмма давления пара над раствором хлороформ – диэтиловый эфир показана на рис.7.

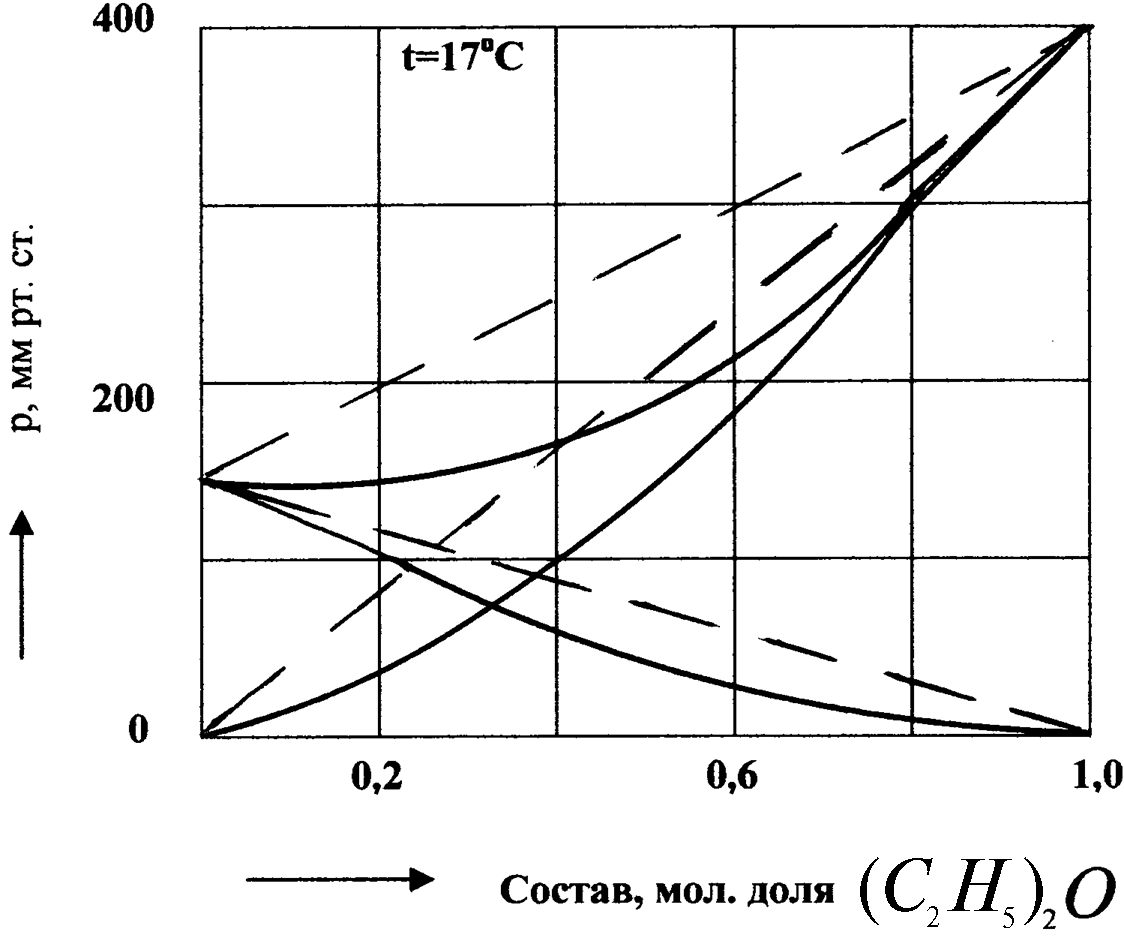
Рис.7. Диаграмма давления пара над раствором (С₂Н₅)₂О – СНСl₃.

Величины общего давления P в этих системах изменяются монотонно с изменением величины х. Если отклонения от закона идеальных растворов велики, то кривая общего давления пара проходит через максимум или минимум.

Положительные и отрицательные отклонения реальных растворов от закона Рауля обусловлены разными факторами. Если разнородные молекулы в растворе взаимно притягиваются с меньшей силой, чем однородные, то это облегчит переход молекул из жидкой фазы в газовую фазу (по сравнению с чистыми жидкостями) и будут наблюдаться положительные отклонения от закона Рауля. Усиление взаимного притяжения разнородных молекул в растворе (сольватация, образование водородной связи, образование химического соединения) затрудняет переход молекул в газовую фазу, поэтому будут наблюдаться отрицательные отклонения от закона Рауля.

Следует иметь в виду, что факторы, вызывающие положительные и отрицательные отклонения, могут действовать в растворе одновременно, поэтому наблюдаемые отклонения часто являются результатом наложения противоположных по знаку отклонений. Одновременное действие противоположных факторов особенно наглядно проявляется в растворах, в которых знак отклонений от закона Рауля – Генри изменяется с изменением концентрации.

§ 4. Диаграммы равновесия жидкость – пар в бинарных системах. Первый закон Коновалова. Фракционная перегонка

На рис.5,6,7 общее давление пара бинарного раствора было представлено как функция состава раствора. В качестве аргумента можно также использовать состав пара, определяемый кривыми парциальных давлений и отличающийся от состава жидкого раствора. Таким путем можно получить вторую кривую того же свойства системы – общего давления насыщенного пара раствора в зависимости от другого аргумента – состава пара.

На рис.8 изображена схематическая диаграмма – изотерма равновесия бинарный раствор – пар. Любая точка на плоскости диаграммы характеризует валовый состав системы (координата х) и давление (координата P) и называется фигуративной точкой. Верхняя кривая отображает зависимость давления насыщенного пара от состава жидкости, а нижняя кривая – зависимость давления насыщенного пара от состава пара. Этими кривыми плоскость диаграммы разделяется на три поля. Верхнее поле охватывает значения х и P, при которых существует только одна жидкая фаза – раствор переменного состава. Нижнее поле отвечает газовой смеси переменного состава. Любая фигуративная точка в верхнем и нижнем полях изображает состояние одной реально существующей фазы. Поле, заключенное между двумя кривыми, соответствует двухфазной системе. Система, давление и состав которой отображает фигуративная точка, находящаяся в этом поле, состоит из двух фаз – раствора и насыщенного пара. Состав этих фаз определяется координатами точек, лежащих на пересечении изобары, проходящей через фигуративную точку системы, с верхней и нижней кривыми. Например, система, характеризуемая фигуративной точкой k, состоит из двух равновесных фаз, состав которых определяется точками а и b. Точка а, лежащая на нижней кривой, характеризует состав насыщенного пара, а точка b, лежащая на верхней кривой,– состав раствора. Нижняя кривая называется ветвью пара, верхняя кривая – ветвью жидкости.

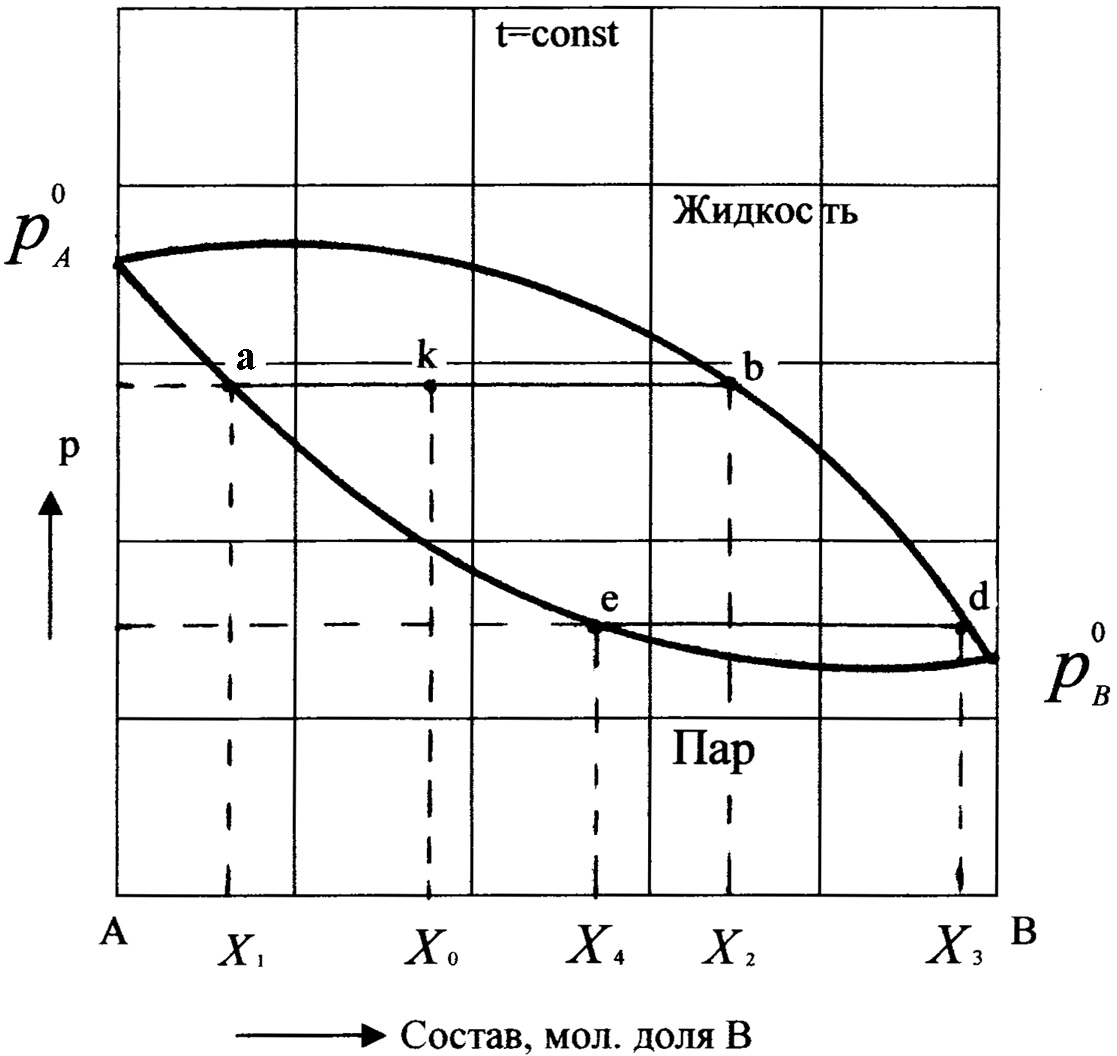
Рис.8. Диаграмма состав – давление бинарной системы.

При изотермическом сжатии ненасыщенного пара состава х₁ фигуративная точка системы движется вверх по вертикали, конденсация пара начинается в точке а (рис.8) при известном значении давления P. Первые капли жидкости имеют состав х₂; образовавшаяся жидкость содержит меньше компонента А, чем конденсирующийся пар.

При изотермическом уменьшении давления жидкость состава х₃ начнет испаряться в точке d, давая пар состава x₄ (точка е); образовавшийся пар содержит больше компонента А, чем испаряющаяся жидкость. Следовательно, в паре всегда преобладает по сравнению с равновесной с ним жидкостью компонент А, прибавление которого к системе, как это видно из диаграммы, увеличивает полное давление пара.

На основании сказанного легко можно сделать следующее заключение: насыщенный пар по сравнению с равновесным раствором относительно богаче тем компонентом, добавление которого к системе повышает полное давление пара. Это – первый закон Коновалова (1881), являющийся справедливым для всех устойчивых растворов.

Рассмотрим явления испарения и конденсации растворов также с помощью изобарной диаграммы температура кипения – состав раствора.

Диаграммы t_кип. – х можно построить по экспериментальным данным, или имея ряд изотермических диаграмм P – х. На каждой диаграмме P – х, построенной при определенной температуре, находят составы сосуществующих раствора и пара при заданном давлении. По полученным из всех изотерм P – х данным для определенного давления строят одну изобарную диаграмму t_кип. – х.

Диаграмма t_кип. – х показана схематически на рис.9. Так как компонент А с более высоким давлением насыщенного пара (рис.8) имеет при данном давлении более низкую температуру кипения ( ), то диаграмма t_кип. – х имеет зеркально-подобный вид по отношению к диаграмме P – х (имеется только качественное подобие).

Верхнее поле на диаграмме t_кип. – х отвечает пару, а нижнее – жидкости. Верхняя кривая – ветвь пара, а нижняя кривая – ветвь жидкости.

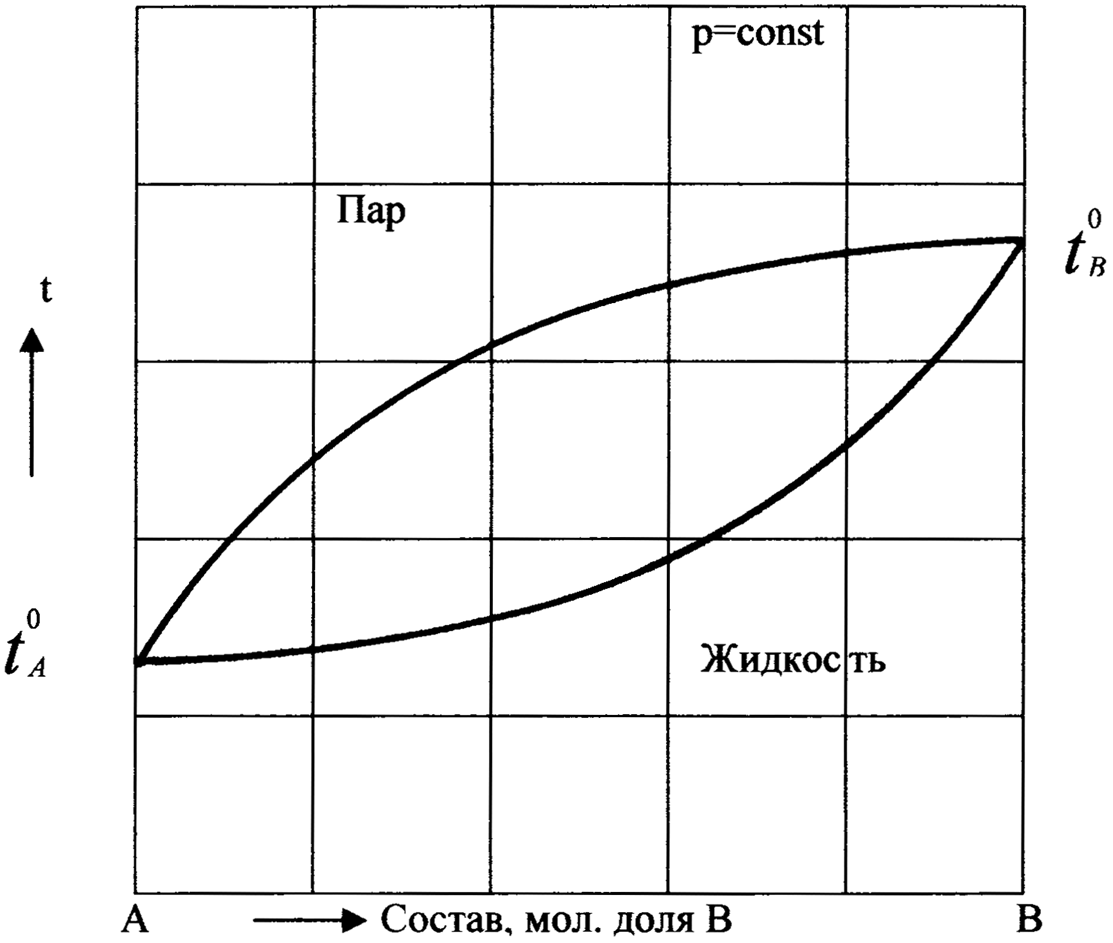
Рис.9. Диаграмма температура кипения – состав бинарной системы.

В ректификационных колоннах последовательные перегонки объединены в один автоматизированный процесс, приводящий к разделению компонентов жидкого раствора (ректификация). Промышленное разделение нефти на фракции (первичная переработка нефти) основано на указанном процессе.

В заключение приведем еще одну формулировку первого закона Коновалова:

В насыщенном паре, находящемся в равновесии с жидким бинарным раствором, выше относительное содержание того компонента, который при T = const имеет более высокое значение давления насыщенных паров по сравнению с другим компонентом или при P = const имеет по сравнению с ним более низкую температуру кипения, иначе говоря, пар по сравнению с жидкостью относительно богаче более летучим компонентом.