3.2 Нахождение экстремумов функции

На основании необходимых и достаточных условий существования экстремумов функции сформулируем

Правило нахождения экстремумов функции

1) Находим частные производные , .

2) Решая систему уравнений 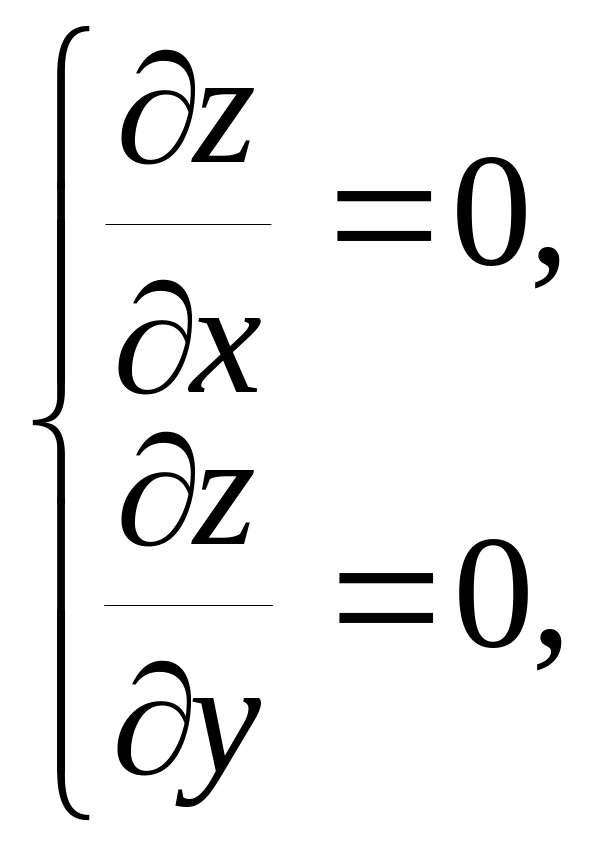определяем критические точки где

3) Находим частные производные второго порядка:

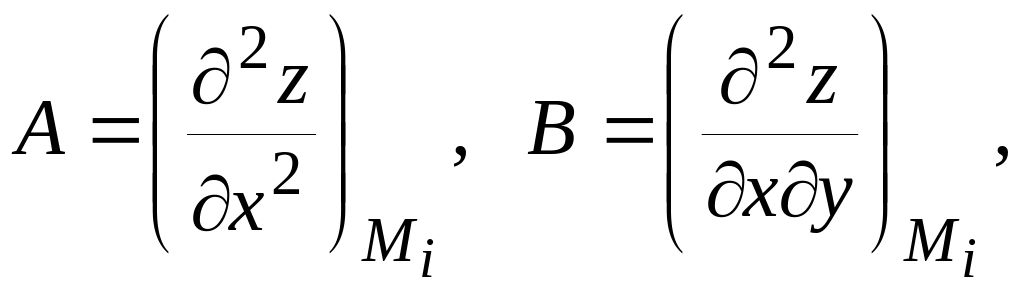
4) Вычисляем значения частных производных второго порядка в каждой критической точке: , а так же значение .

Если , то экстремум в точке М_i есть, причем, при - максимум, при - минимум; если экстремума в точке М_i нет. В случае, когда необходимо решать вопрос о наличии экстремума с помощью дополнительных исследований.

5) Находим экстремумы (экстремальные значения) функции.

Пример 3.1 Найти экстремумы функции

Решение. 1) Найдем частные производные

2) Определим критические точки, решив систему уравнений:

Следовательно, М₁(3;6) и М₂ (-3;-6) – критические точки.

3) Найдем частные производные второго порядка:

4) Вычислим значения частных производных второго порядка в каждой критической точке и решим вопрос о наличие экстремума в ней:

- для точки М₁(3;6)

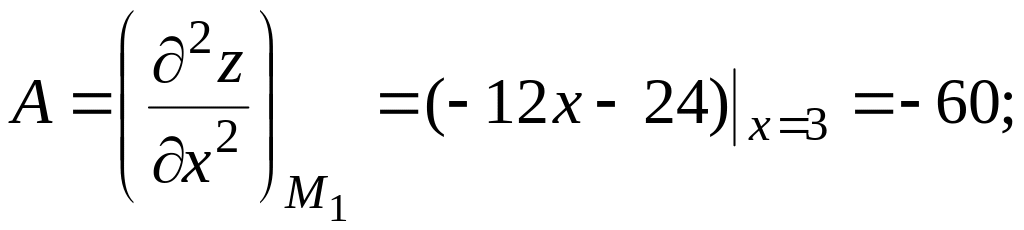
Тогда следовательно, в точке М₁ экстремум есть, и так как А < 0, то М₁ – точка максимума;

- для точки М₂ (-3;-6)

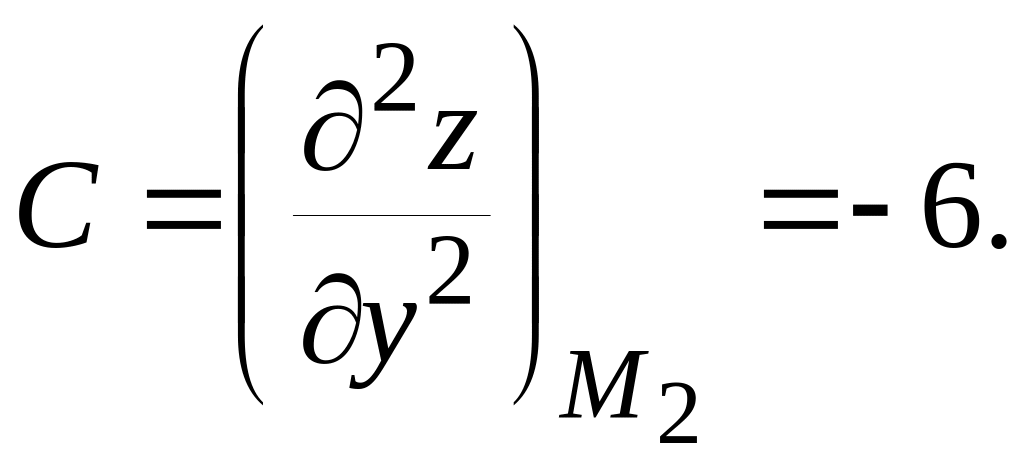
Тогда Отсюда следует, что в точке М₂ экстремума нет.

5) Определяем экстремум функции, то есть ее максимум:

Пример 3.2 Производственная функция в денежном выражении имеет вид ( – количество единиц первого ресурса; - второго). Стоимость единицы первого ресурса – 5, а второго – 10 денежных единиц. Найдите значения величин используемых ресурсов , при которых фирма-производитель получит максимальную прибыль и значение этой прибыли.

Решение. Производственной функцией называется зависимость результата производственной деятельности – выпуска продукции от обусловивших его факторов – затрат ресурсов. Если эта функция задана в виде

(3.1)

то она называется функцией Кобба-Дугласа, в которой параметры и показывают приближенно, на сколько процентов изменится переменная при изменении на 1 %.

Обозначим издержки производства , тогда прибыль составит:

Требуется найти те значения затрат ресурсов и , при которых прибыль достигнет максимума.

Найдем частные производные:

.

Приравнивая их к нулю, определяем критические точки:

Отсюда получаем, что или

- посторонний корень, т.к. по смыслу задачи тогда

. Следовательно, точка - критическая.

Находим частные производные второго порядка:

;

;

.

Вычислим значения этих производных в точке :

.

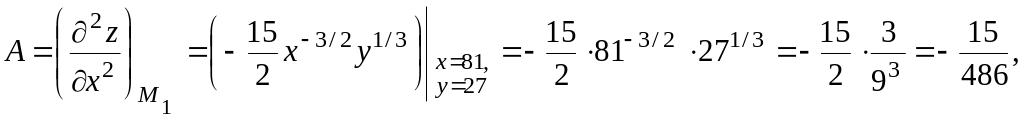
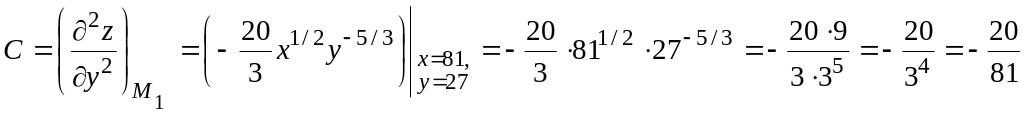Тогда

Следовательно, в точке функция имеет экстремум и так как то это максимум.

Найдем максимальную прибыль фирмы-производителя, которую она достигнет, если истратит 81 единицу первого сырья и 27 единиц – второго:

(ден. единиц)

3.3 Вопросы для самопроверки

1. Какие точки называют точками максимума (минимума) функции ?

2. Какое из нижеприведенных утверждений верно:

а) - точка экстремума ;

б) - точка экстремума?

3. Как формулируются достаточные условия существования экстремума функции ?

4. По какому правилу находят экстремумы функции ?

5. Если в некоторой точке функции значения частных производных второго порядка 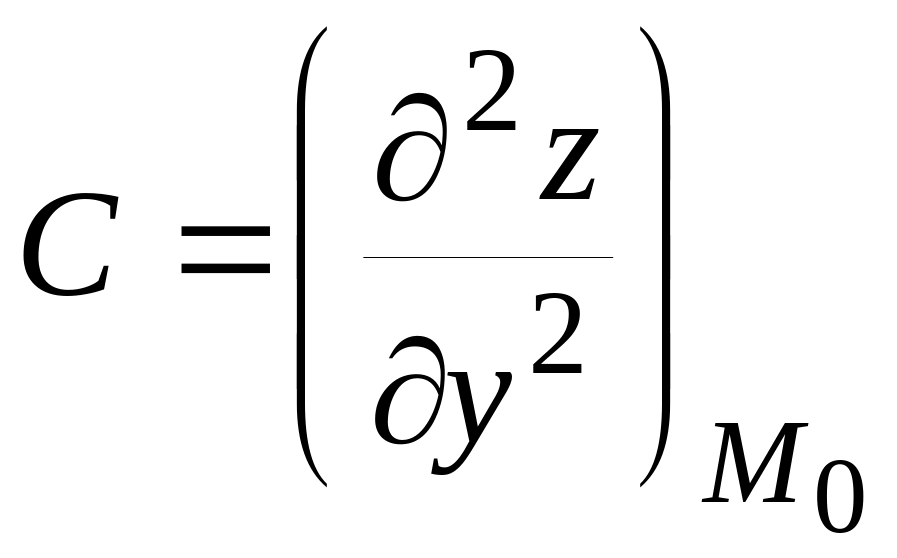равны:

а) А = -2; В = 4; С = -10; б) А = 4; В = 3; С = 0; в) А = 2; В = -3; С = 5, то что можно сказать о наличии экстремума и его виде в этой точке?