2.4 Вопросы для самопроверки

1. Что называют частной производной для функции ?

2. В чем состоит геометрический смысл ; ?

3. В чем разница нахождений производных функции от ?

4. Как находят дифференциал первого порядка для функции ?

5. Расскажите о порядке дифференцирования и по какой переменной, при нахождении .

6. Как определяют дифференциал второго порядка функции ?

2.5 Вопросы для самостоятельной работы

С помощью рекомендуемой литературы [1, 2] изучите и законспектируйте тему: «Применение полного дифференциала функции к приближенным вычислениям».

Лекция 3

Тема: Экстремумы функции

3.1 Экстремумы функции : основные понятия и теоремы

3.2 Нахождение экстремумов функции

3.3 Вопросы для самопроверки

3.1 Экстремумы функции : основные понятия и теоремы

Как и в случае функции одной переменной, функция имеет некоторые точки, которые определяют структуру ее графика. В первую очередь, это точки экстремума.

О пределение. Точка называется точкой максимума (минимума) функции , если существует окрестность этой точки, что для всех точек из этой окрестности выполняется неравенство

. (3.1)

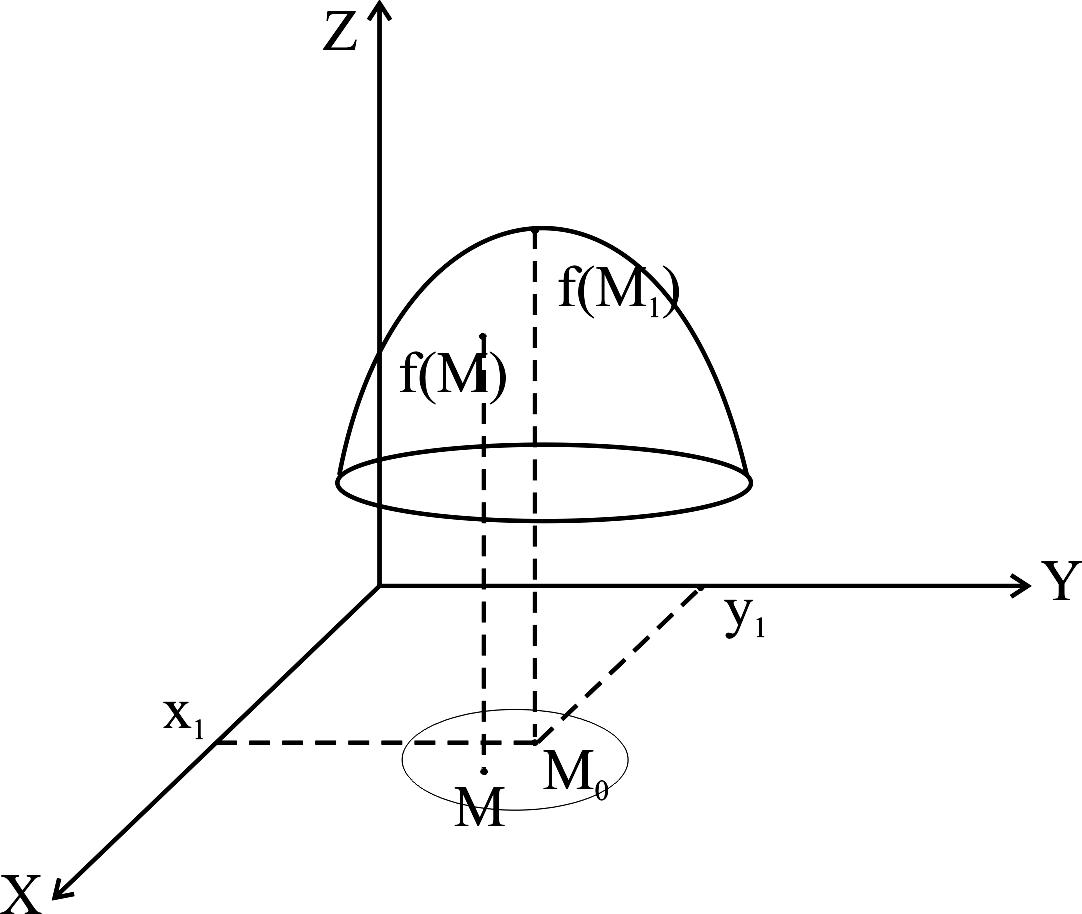
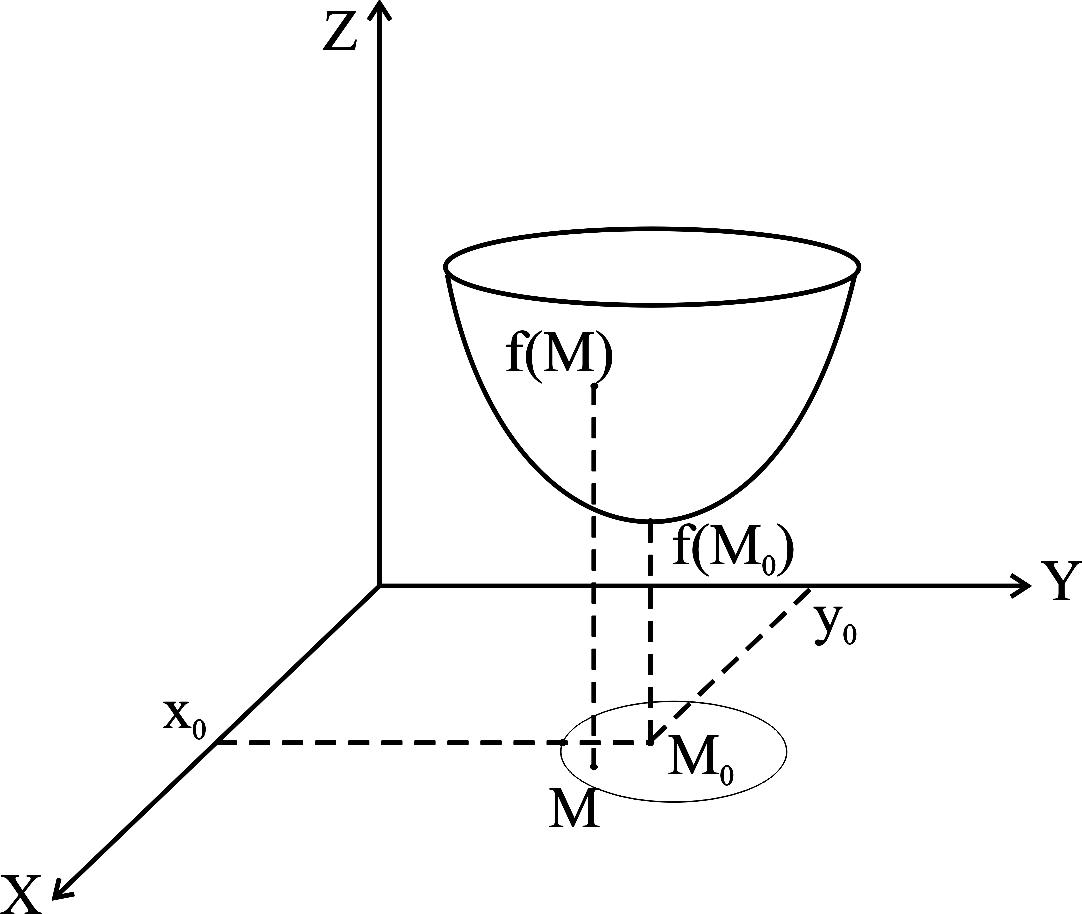
На рисунке 7 а) точка М₀ – есть точка минимума, а точка - точка максимума (рисунок 7,б)

1

а) б)

Рисунок 7

Точки максимума и минимума, как и прежде, называем точками экстремума, а значения функции в них – экстремумами функции. Экстремумы функции носят локальный характер, так как речь идет о максимальном или минимальном значении лишь в достаточно малой окрестности точки

Так же, как и для функции одной переменной, можно сформулировать необходимое условие существования экстремума для функции .

Т еорема Если точка - точка экстремума дифференцируемой функции , то ее частные производные в этой точке равны нулю.

Доказательство. Пусть, например, - точка максимума. Зафиксируем одну из переменных, например , полагая, что . Тогда функция станет функцией одной переменной , которая, очевидно, имеет максимум при . На основании необходимого условия существования экстремума функции одной переменной имеем, что или . Аналогично можно доказать, что и , ч.т.д.

Заметим, что функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует.

Например, функция , очевидно, имеет минимум в точке (0,0), но ее частные производные и в этой точке не существуют

О пределение. Точки, в которых частные производные и функции равны нулю или не существуют, будем называть критическими точками этой функции.

Однако из равенства нулю частных производных в некоторой точке, в общем случае не следует, что функция в этой точке имеет экстремум. Так, например, на рисунке 8 изображена, так называемая, седловая точка .

Рисунок 8

Частные производные в этой точке равны нулю, но, как следует из рисунка 8, никакого экстремума в точке нет. Такие седловые точки являются двумерными аналогами точек перегиба функции одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Для этого нужны достаточные условия существования экстремума, которые мы сформулируем без доказательства.

Т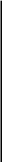 еорема. Пусть функция определена в некоторой окрестности критической точки , а в самой точке имеет непрерывные частные производные второго порядка

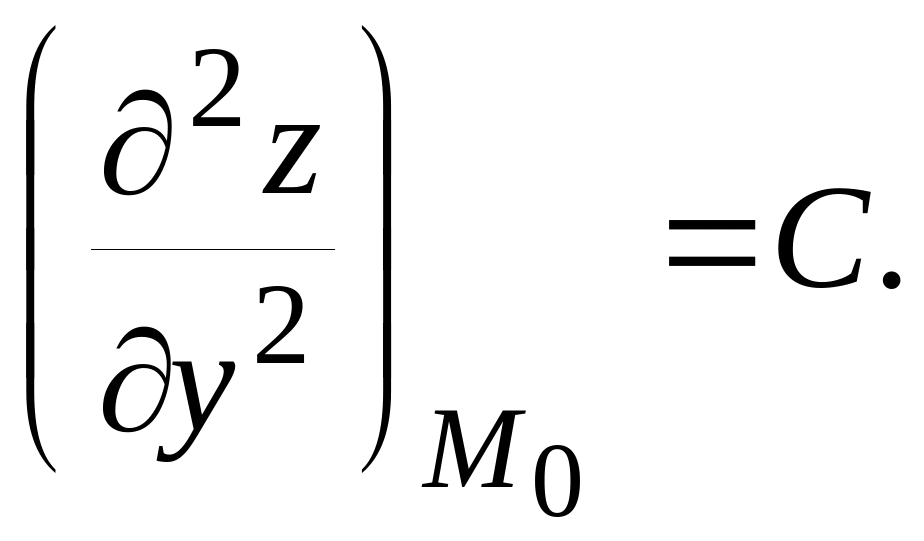Тогда, если то в точке функция имеет экстремум, причем, если - максимум, если - минимум. Если же то экстремума нет. В случае вопрос о наличии экстремума остается открытым (необходимы дополнительные исследования).