2.2 Дифференциал функции

Для функции одной переменной дифференциал определялся как главная часть ее приращения, линейная относительно , при этом .

Обобщая определение дифференциала функции на случай функции , можно дать следующее аналогичное определение.

О пределение. Главная часть полного приращения функции , линейная относительно приращений аргументов и , называется полным

дифференциалом этой функции и обозначается символом :

. (2.5)

Так как для независимых переменных x и y приращения совпадают с их дифференциалами, то есть , , равенство (2.5) можно записать в виде: .

В более полных курсах математики доказывается, что , . Тогда окончательно можно записать формулу для определения дифференциала функции :

. (2.6)

Для функции одной переменной понятие ее дифференцируемости определялось через существование производной. Для функции нескольких переменных дело обстоит иначе: существование частных производных является лишь необходимым, но не достаточным условием дифференцируемости функции.

Следующая теорема выражает достаточное условие дифференцируемости функции , которую мы примем без доказательства.

Т еорема. Если частные производные функции , существуют в окрестности точки (x, y) и непрерывны в самой точке (x, y), то функция

дифференцируема в этой точке.

2.3 Частные производные и дифференциалы высших порядков

При нахождении частных производных и мы видим, что результат дифференцирования также является функцией двух переменных. Эти функции, в свою очередь, могут иметь частные производные, которые мы будем называть вторыми частными производными (или частными производными второго порядка) исходной функции.

Следовательно, функция имеет четыре частных производных второго порядка, которые определяются и обозначаются следующим образом:

; ;

; .

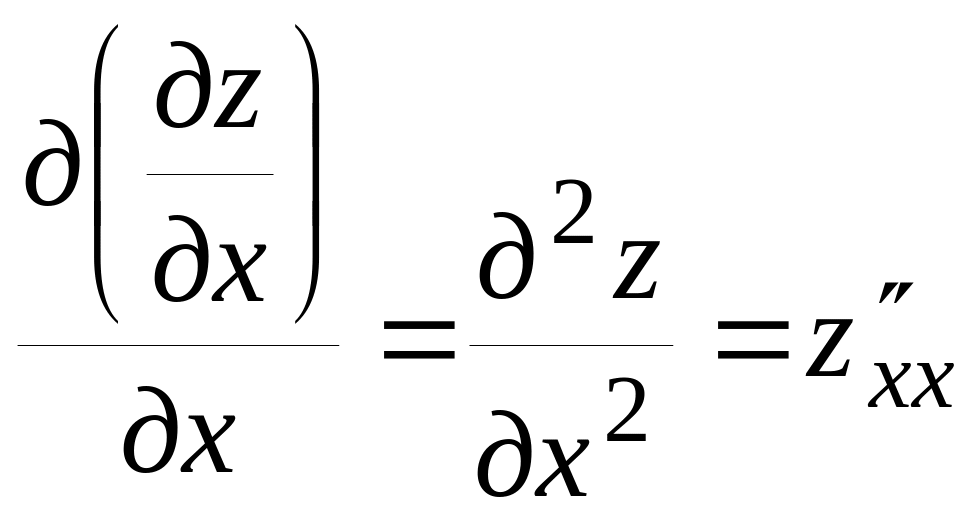Аналогично определяются и обозначаются частные производные третьего и более высокого порядка.

Определение. Частной производной n-го порядка функции нескольких пе-

ременных называется частная производная первого порядка от частной

производной (n-1)-го порядка той же функции.

Например, частная производная третьего порядка функции есть частная производная первого порядка по y от частной производной второго порядка :

.

Определение. Частная производная второго или более высокого порядка,

взятая по нескольким различным переменным, называется смешанной

част ной производной.

Например, частные производные функции , , , являются смешанными частными производными функции двух переменных .

Пример 2.3 Найти частные производные второго порядка функции .

Решение. Находим частные производные первого порядка:

;

Затем находим частные производные второго порядка:

; ;

;

Мы видим, что смешанные частные производные и , отличающиеся между собой лишь порядком дифференцирования, оказались тождественно равными. Этот результат не случаен. Относительно смешанных частных производных имеет место следующая теорема, которую мы принимаем без доказательства.

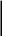Теорема. Две смешанные частные производные одной и той же функции,

отличающиеся лишь порядком дифференцирования, равны между собой при

условии их непрерывности.

(2.7)

Так же, как и для функции одной переменной, для функции вводится и понятие дифференциалов высших порядков.

Определение. Полным дифференциалом n-го порядка называется полный

дифференциал от полного дифференциала (n-1)-го порядка:

. (2.8)

В частности, . Пользуясь формулой для вычисления дифференциала первого порядка (2.6) и теоремой о смешанных частных производных, получим формулу для дифференциала второго порядка.

. Таким образом,

(2.9)

Пример 2.4 Для функции найти дифференциал второго порядка .

Решение. Для нахождения найдем все необходимые частные производные: ; ;

; ;

.

Следовательно, .