16.3 Разложение некоторых элементарных функций в ряд
Маклорена
а) Разложение
в степенной ряд функции
Разложим
в
ряд Маклорена (16.4). Для этого найдем
значения функции и ее производных при
x
= 0.
,
,
,
…
.
Напишем ряд
Маклорена:
и найдем область его сходимости.
,
.
Следовательно, ряд сходится на всей числовой оси.
Можно показать,
что на интервале
сумма ряда совпадает с функцией
.
Итак, на всей числовой оси имеет место
разложение:
(16.8)
В дальнейшем при разложении функций в степенной ряд будем устанавливать вид ряда и его область сходимости, а доказательства стремления к нулю остаточного члена опускаем из-за их сложности.
б)
Разложение в степенной ряд функции
Имеем
,
,
,
,
.
При x
= 0 получаем,
что
,
,
,
,
Очевидно, что
производные четного порядка
,
а нечетного порядка
.
Тогда по формуле (16.4) получим для функции
sin
x
следующий ряд Маклорена:
.
Для установления области сходимости рассмотрим ряд из абсолютных величин членов, к которому применим признак Даламбера:
Следовательно, ряд сходится абсолютно при всех x, то есть область сходимости – вся числовая прямая. Тогда имеем:
(16.9)
Аналогично можно получить разложение в ряд Маклорена следующих функций (сделайте это самостоятельно):
(16.10)
(16.11)
(16.11) называется биномиальным рядом.
(16.12)
Для улучшения сходимости ряда (16.12) и возможности его использования при вычислении логарифмов любых чисел используют разложение:
(16.13)
16.4 Применение рядов к приближенным вычислениям
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения. Связь основных элементарных функций с многочленами используется при вычислении их значений на калькуляторе или ПК.
Пример 16.1 Вычислить приближенно с точностью до 0,0001:
а)
;
б)
.
Решение.
а)
Для вычисления
запишем разложением в ряд Маклорена
функции
.
,
в котором заменим x
на
:
или
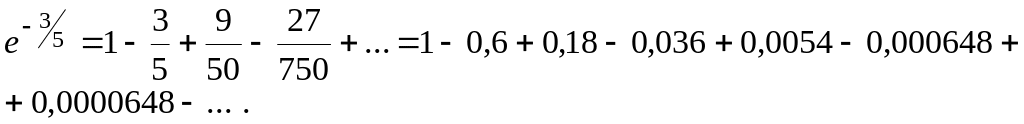
В получившимся знакочередующимся ряде члены ряда монотонно убывают по абсолютной величине и стремятся к нулю, поэтому его остаток не будет превосходить первого отброшенного члена.
Так как седьмой член ряда, равный 0,0000648 меньше заданной точности 0,0001, то
.
б) Вычислить данный интеграл в элементарных функциях не представляется возможным, так как он «неберущийся». Поэтому попытаемся разложить подынтегральную функцию в ряд Маклорена.
Используя разложение
для
,
в котором заменим x
на (-x),
мы получим:
.
Умножая полученный
ряд на
и почленно интегрируя в интервале (0; 1), принадлежащем интервалу сходимости ряда , получим
.
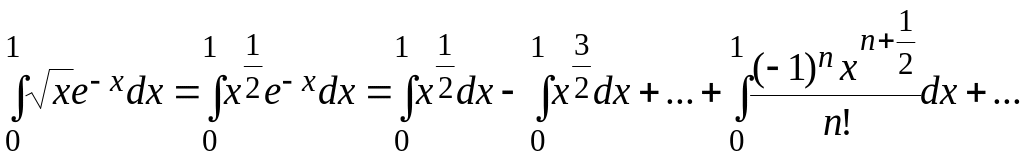
Оценка погрешности вычисления производится
так же, как и в примере 16.1, а.
При помощи разложений функций в степенные ряды можно приближенно интегрировать разнообразные дифференциальные уравнения. При этом решение уравнения представляют в виде ряда Тейлора (или Маклорена, что зависит от задания x = x0), тогда сумма ряда будет приближенно равняться искомому частному решению.
Пусть, например,
требуется найти решение дифференциального
уравнения первого порядка
, (16.14)
удовлетворяющее
начальному условию
.
(16.15)
Предположим, что
решение
существует
и представимо в виде ряда Тейлора (мы
не будем останавливаться на условиях,
при которых это возможно):
(16.16)
Тогда необходимо
найти значение
,
,
,
что возможно при помощи уравнения
(16.14) и начального условия (16.15). В самом
деле, из условия (16.15) следует, что
,
а из условия (16.14) получаем
.
Дифференцируя
обе части уравнения (16.14) по x
и, подставляя значения
,
,
,
найдем
.
Полученное соотношение дифференцируют
еще раз, находят
и т.д.
Найденные значения производных подставляют в равенство (16.16). Для тех значений x, для которых этот ряд сходится, он представляет решение уравнения.
Пример 16.2
Найти решение уравнения
(16.17)
при начальных
условиях
,
.
(16.18)
Решение. Так как начальные условия заданы при x = 0, то будем искать решение этого уравнения в виде ряда Маклорена:
(16.19)
Из начальных
условий (16.18) имеем:
,
,
а из уравнения (16.17) получаем
.
Дифференцируем обе части уравнения по
x:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Нетрудно заметить,
что отличны от нуля лишь производные,
порядок которых кратен трем, причем
,
,
,
.
Таким образом, получаем ряд
(16.20)
Для нахождения
его области сходимости применим признак
Даламбера:
при любом x.
Следовательно, ряд (16.20) сходится при всех значениях x и его сумма приближенно равна частному решению дифференциального уравнения.