
- •080502 – „Экономика и управление на предприятии”
- •080507 – „Менеджмент организации”
- •050501.18 – „Профессиональное обучение (экономика и управление)”
- •Содержание
- •Лекция 1
- •1.1 Функции двух и нескольких переменных: основные понятия
- •1.2 Способы задания функции двух переменных
- •1.3 Предел и непрерывность функции
- •1.4 Частные и полное приращения функции двух переменных.
- •1.5 Вопросы для самопроверки
- •1.6 Вопросы для самостоятельной работы.
- •Лекция №2
- •2.1 Частные производные первого порядка функции
- •2.2 Дифференциал функции
- •2.3 Частные производные и дифференциалы высших порядков
- •2.4 Вопросы для самопроверки
- •2.5 Вопросы для самостоятельной работы
- •Лекция 3
- •3.1 Экстремумы функции : основные понятия и теоремы
- •3.2 Нахождение экстремумов функции
- •3.3 Вопросы для самопроверки
- •Лекция 4
- •4.1 Понятие первообразной и неопределенного интеграла
- •4.2 Геометрический смысл неопределенного интеграла
- •40. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, т.Е.
- •50.Постоянный множитель можно выносить за знак интеграла, т.Е.
- •4.4 Таблица правил и формул интегрирования
- •Правила интегрирования
- •4.5 Вопросы для самопроверки
- •Лекция № 5
- •Метод интегрирование по частям
- •5.2 Метод замены переменной
- •Этапы замены переменной в неопределенном интеграле
- •5.3 Интегрирование функций, содержащих квадратный трехчлен
- •5.4 Интегрирование некоторых видов иррациональностей
- •1 0. Интегралы от рациональных выражений, содержащих корни различных степеней из :
- •20. Интегралы от рациональных выражений, содержащих корни различных степеней из :
- •5.5 Понятие о «неберущихся» интегралах
- •5.6 Вопросы для самопроверки
- •5.7 Вопросы для самостоятельной работы
- •Лекция № 6
- •6.1 Задачи, приводящие к понятию определенного интеграла:
- •6.2 Интегральная сумма. Понятие определенного интеграла
- •6.3 Геометрический смысл определенного интеграла
- •6.4 Экономический смысл определенного интеграла
- •40. Определенный интеграл от функции тождественно равной единице, равен длине отрезка интегрирования:
- •6.6 Вопросы для самопроверки
- •6.7 Вопросы для самостоятельной работы
- •Лекция №7
- •7.1 Вычисление определенного интеграла по формуле
- •7.2 Метод интегрирования по частям в определенном интеграле
- •7.3 Замена переменной в определенном интеграле
- •7.4 Вопросы для самопроверки
- •7.5 Вопросы для самостоятельной работы
- •Лекция №8
- •8.1 Вычисление площадей плоских фигур
- •8.2 Нахождение объемов тел вращения
- •8.3 Несобственные интегралы
- •I) Несобственные интегралы с бесконечными пределами интегрирования
- •II) Несобственные интегралы от разрывных функций.
- •8.4 Вопросы для самопроверки
- •Лекция 9
- •9.1 Основная идея численных методов вычисления приближенного
- •9.2 Метод прямоугольников
- •9.3 Метод трапеций
- •9.4 Метод Симпсона
- •9.5 Вопросы для самопроверки
- •9.6 Вопросы для самостоятельной работы
- •Лекция 10
- •10.1 Задачи, приводящие к дифференциальным уравнениям
- •10.2 Дифференциальные уравнения первого порядка:
- •10.3 Дифференциальные уравнения с разделенными переменными
- •10.4 Дифференциальные уравнения с разделяющимися
- •10.5 Вопросы для самопроверки
- •10.6 Вопросы для самостоятельной работы
- •Лекция 11
- •11.1 Линейные дифференциальные уравнения 1-го порядка.
- •11.5 Вопросы для самопроверки
- •Лекция № 12
- •12.1 Линейные дифференциальные уравнения второго порядка
- •12.2 Однородные линейные дифференциальные уравнения второго
- •Понятие о комплексных числах
- •12.3 Вопросы для самопроверки
- •12.4 Вопросы для самостоятельной работы
- •Лекция №13
- •13.1 Нахождение общего решения нлу 2-го порядка
- •13.2 Метод подбора частного решения нлу в случае, когда правая
- •13.3 Метод подбора частного решения нлу в случае, когда правая
- •13.4 Теорема о наложении решений
- •13.5 Вопросы для самопроверки
- •13.6 Вопросы для самостоятельной работы
- •Лекция №14
- •14.1 Определение числового ряда и его сходимости
- •14.2 Свойства сходящихся рядов
- •14.3 Необходимый признак сходимости и его следствие
- •14.4 Вопросы для самопроверки
- •14.5 Вопросы для самостоятельной работы
- •Лекция №15
- •15.1 Достаточные признаки сходимости рядов с положительными
- •15.2 Знакопеременные ряды. Достаточный признак сходимости
- •15.3 Знакочередующиеся ряды. Признак Лейбница
- •15.4 Функциональные ряды. Область сходимости степенного ряда
- •15.5 Степенные ряды. Нахождение области сходимости степенного
- •15.6 Вопросы для самопроверки
- •15.7 Вопросы для самостоятельной работы
- •Лекция №16
- •16.1 Разложение функций в степенные ряды
- •16.2 Ряды Тейлора и Маклорена
- •16.3 Разложение некоторых элементарных функций в ряд
- •16.4 Применение рядов к приближенным вычислениям
- •16.5 Вопросы для самопроверки
- •16.6 Вопросы для самостоятельной работы
- •Рекомендуемая литература
- •Функции нескольких переменных. Интегральное исчисление. Дифференциальные уравнения. Ряды
- •080502 – „Экономика и управление на предприятии”
- •080507 – „Менеджмент организации”
- •050501.18 – „Профессиональное обучение (экономика и управление)”
14.2 Свойства сходящихся рядов
Т еорема
1 (об умножении ряда на число).
Если ряд
сходится
и имеет сумму S,
то ряд
еорема
1 (об умножении ряда на число).
Если ряд
сходится
и имеет сумму S,
то ряд
![]() ,
где
,
где
![]() - произвольное число, сходится, и его
сумма равна
- произвольное число, сходится, и его
сумма равна
![]() .
.
Доказательство.
Рассмотрим ряд
и
его n-ую
частичную сумму
![]() .
Так как ряд сходится, то, по определению,
.
Так как ряд сходится, то, по определению,
![]() .
Для ряда
,
все члены которого получены из членов
исходного ряда путем умножения на одно
и то же число с,
n-ая
частичная сумма
.
Для ряда
,
все члены которого получены из членов
исходного ряда путем умножения на одно
и то же число с,
n-ая
частичная сумма
![]() .
.
Тогда
![]() - конечен и, следовательно, ряд
сходится,
а его сумма равна
- конечен и, следовательно, ряд
сходится,
а его сумма равна
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Последующие свойства рядов приведем без доказательства.
 Теорема
2 (о сложении рядов).
Если ряды
Теорема
2 (о сложении рядов).
Если ряды
![]() и
и
![]() сходятся и их суммы соответственно
равны
сходятся и их суммы соответственно
равны
![]() и
и
![]() , то ряд
, то ряд
![]() также сходится, и его сумма
также сходится, и его сумма
![]() .
.
Теорема 3 (об игнорировании первых членов ряда). Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания конечного числа m его первых членов.
Теорему 3 можно сформулировать иначе так: на сходимость ряда не влияет отбрасывает любого конечного числа его первых членов.
14.3 Необходимый признак сходимости и его следствие
Теорема.
Если ряд
сходится,
то предел его общего члена
![]() при
при
 равен нулю, то
есть:
равен нулю, то
есть:
![]() . (14.14)
. (14.14)
Доказательство.
Рассмотрим n-ую
частичную сумму ряда
![]() ,
тогда
,
тогда
![]() ,
где
,
где
![]() - частичная сумма (n-1)
–го членов ряда. Так как ряд сходится,
то
и
- частичная сумма (n-1)
–го членов ряда. Так как ряд сходится,
то
и
![]() .
Поэтому
.
Поэтому
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Следствие (достаточный признак сходимости ряда). Если предел общего
члена ряда при не равен нулю, то ряд расходится, то есть:

![]() (14.15)
(14.15)
Доказательство.
Предположим противное, то есть ряд
сходится,
но тогда на основании необходимого
признака сходимости имеем, что
![]() ,
а это условие противоречит условию,
заданному в следствии
,
а это условие противоречит условию,
заданному в следствии
![]() .
Следовательно, наше предположение
неверно, и ряд расходится, что и требовалось
доказать.
.
Следовательно, наше предположение
неверно, и ряд расходится, что и требовалось
доказать.
Замечание.
Доказанная теорема выражает лишь
необходимый,
но не достаточный
признак сходимости ряда:
![]() - сходится.
- сходится.
 В
качестве примера рассмотрим ряд
В
качестве примера рассмотрим ряд
![]() (14.16)
(14.16)
который называется гармоническим.
Для этого ряда
![]() ,
но можно доказать, что он расходится. С
этой целью запишем частичные суммы n
и 2n
первых членов ряда:
,
но можно доказать, что он расходится. С
этой целью запишем частичные суммы n
и 2n
первых членов ряда:
![]() ;
;
![]() .
.
Найдем разность
![]() .
В полученной справа сумме заменим каждое
слагаемое на наименьшее из них, то есть
на
.
В полученной справа сумме заменим каждое
слагаемое на наименьшее из них, то есть
на
![]() .
Тогда имеем:
.
Тогда имеем:
![]() >
>
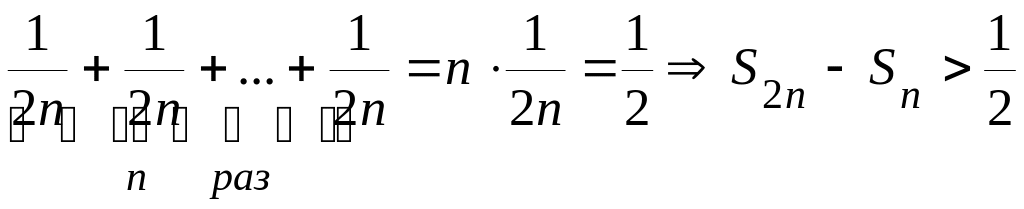 .
(14.17)
.
(14.17)
Предположим
противное, что гармонический ряд
сходится, тогда
![]() .
Переходя к пределу в неравенстве (14.17),
получим
.
Переходя к пределу в неравенстве (14.17),
получим
![]() .
.
Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, то есть гармонический ряд расходится.
14.4 Вопросы для самопроверки
Как определяется числовой ряд?
Какой ряд называется сходящимся? расходящимся?
Какими свойствами обладают сходящиеся числовые ряды?
Известно, что ряд
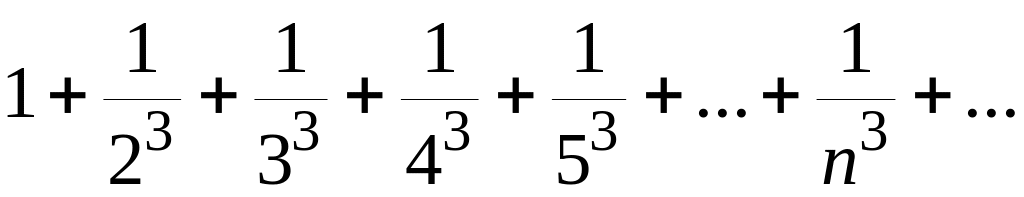 сходится.
сходится.
Как ведут себя
ряды: а)![]() ;
;
б)![]() ?
?
Как связан предел общего члена со сходимостью (расходимостью)
ряда?
Какой ряд называется гармоническим и как он себя ведет?
Если
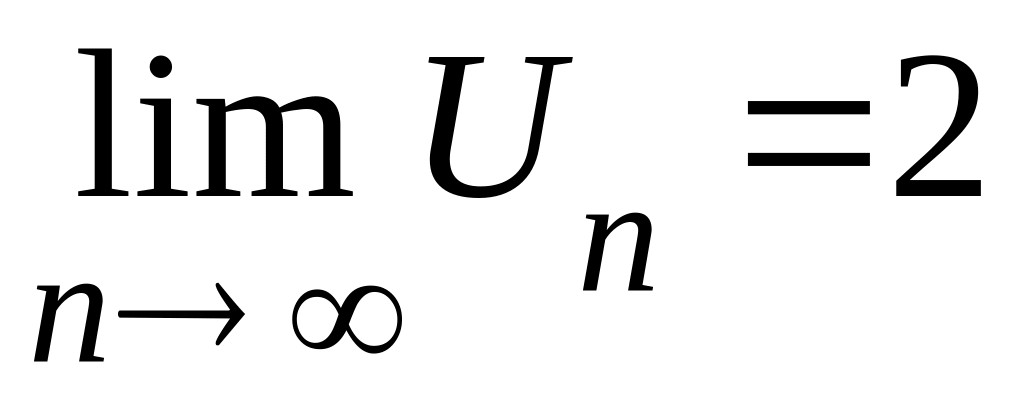 или
или
 или
,
то как ведет
или
,
то как ведет
себя соответствующий ряд?
