13.3 Метод подбора частного решения нлу в случае, когда правая
часть имеет вид
(13.7)
где M, N, γ, ω – некоторые числа.
Тогда можно показать, что частное решение уравнения:
(13.8)
с
ледует
искать в виде:
(13.9)
где А, В – неизвестные коэффициенты.
З
амечание.
Вид частного решения
сохраняется и в том случае, когда в
правой части уравнения (13.8) один из
коэффициентов М
или N
равен нулю, то есть когда правая часть
уравнения имеет вид:
или
.
Пример 13.2
Найти частное решение уравнения
,
удовлетворяющего начальным условиям
.
Решение. Общее решение данного уравнения представляет собой сумму общего решения соответствующего однородного уравнения и частного решения исходного НЛУ:
.
1)
- общее решение уравнения
.
Составим характеристическое уравнение
,
корни которого равны:
.
Тогда
имеет вид: 
.
2) Запишем частное решение уравнения
по виду правой части с учетом (13.9):
,
т.к. ω =
0; γ
= 1 и
.
Тогда
,
.
Подставим и в левую часть уравнения:
или
.
Два тригонометрических многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых тригонометрических функциях.
Сравним коэффициенты:
Следовательно,
.
Тогда
- общее решение.
Найдем
частное решение, удовлетворяющее
начальным условиям
,
.
.
Так как
,
то из
следует, что
.
Имеем
- частное решение,
удовлетворяющее заданным начальным
условиям.
13.4 Теорема о наложении решений
В некоторых задачах правая часть НЛУ представляет собой алгебраическую сумму нескольких функций.
Тогда частное решение находят, опираясь на следующую теорему.
Теорема (о
наложении решений).
Если правая часть f(x) уравнения (13.1) является суммой некоторых
функций, то есть
,
то частное решение
такого уравнения
представляет собой сумму частных решений
уравнений
,
то есть
(13.10)
Теорема доказывается подстановкой (13.10) в уравнение (13.1).
Покажем на примере использование указанной теоремы.
Пример 13.3 Найти общее решение уравнения
.
Решение. Общее решение данного уравнения y равно: ,
где - общее решение соответствующего однородного уравнения;
- частное решение исходного неоднородного линейного уравнения.
Так
как правая часть уравнения состоит из
трех различных функций
;
;
,
то
,
где
- частные решения данного уравнения,
когда справа стоит одна из функций
.
1) Найдем
.
Для этого составим характеристическое
уравнение и решим его: 
;
.
Следовательно,
.
2) Определим как решение уравнения:
.
Тогда по виду правой части форма запишется так:
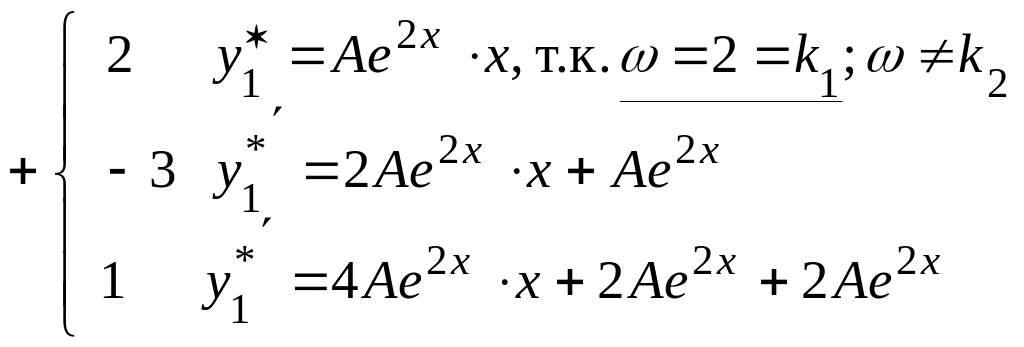
Складывая
строчки, умноженные на числа, стоящие
за чертой, мы получим левую часть
уравнения. Приравняем ее к правой части
и сократим на
.
Сравниваем коэффициенты при одинаковых
степенях x:
при x
свободные
члены
Тогда
.
3) Найдем
как решение уравнения:
.
Тогда 2
,
-3
1
Сравниваем коэффициенты при одинаковых степенях x в многочленах, стоящих в левой и правой частях уравнения:
при
x2
при x
свободные
члены
Следовательно,
.
4) Определим
как решение уравнения: 
.
2
,
т.к.
-3
1
Сравниваем в тригонометрических многочленах слева и справа коэффициенты, стоящие при одинаковых тригонометрических функциях
при
cos2x
при sin2x
Решим полученную систему уравнений для определения коэффициентов А и В:
.
Следовательно,
.
Тогда общее решение исходного уравнения имеет вид:
.