
- •080502 – „Экономика и управление на предприятии”
- •080507 – „Менеджмент организации”
- •050501.18 – „Профессиональное обучение (экономика и управление)”
- •Содержание
- •Лекция 1
- •1.1 Функции двух и нескольких переменных: основные понятия
- •1.2 Способы задания функции двух переменных
- •1.3 Предел и непрерывность функции
- •1.4 Частные и полное приращения функции двух переменных.
- •1.5 Вопросы для самопроверки
- •1.6 Вопросы для самостоятельной работы.
- •Лекция №2
- •2.1 Частные производные первого порядка функции
- •2.2 Дифференциал функции
- •2.3 Частные производные и дифференциалы высших порядков
- •2.4 Вопросы для самопроверки
- •2.5 Вопросы для самостоятельной работы
- •Лекция 3
- •3.1 Экстремумы функции : основные понятия и теоремы
- •3.2 Нахождение экстремумов функции
- •3.3 Вопросы для самопроверки
- •Лекция 4
- •4.1 Понятие первообразной и неопределенного интеграла
- •4.2 Геометрический смысл неопределенного интеграла
- •40. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, т.Е.
- •50.Постоянный множитель можно выносить за знак интеграла, т.Е.
- •4.4 Таблица правил и формул интегрирования
- •Правила интегрирования
- •4.5 Вопросы для самопроверки
- •Лекция № 5
- •Метод интегрирование по частям
- •5.2 Метод замены переменной
- •Этапы замены переменной в неопределенном интеграле
- •5.3 Интегрирование функций, содержащих квадратный трехчлен
- •5.4 Интегрирование некоторых видов иррациональностей
- •1 0. Интегралы от рациональных выражений, содержащих корни различных степеней из :
- •20. Интегралы от рациональных выражений, содержащих корни различных степеней из :
- •5.5 Понятие о «неберущихся» интегралах
- •5.6 Вопросы для самопроверки
- •5.7 Вопросы для самостоятельной работы
- •Лекция № 6
- •6.1 Задачи, приводящие к понятию определенного интеграла:
- •6.2 Интегральная сумма. Понятие определенного интеграла
- •6.3 Геометрический смысл определенного интеграла
- •6.4 Экономический смысл определенного интеграла
- •40. Определенный интеграл от функции тождественно равной единице, равен длине отрезка интегрирования:
- •6.6 Вопросы для самопроверки
- •6.7 Вопросы для самостоятельной работы
- •Лекция №7
- •7.1 Вычисление определенного интеграла по формуле
- •7.2 Метод интегрирования по частям в определенном интеграле
- •7.3 Замена переменной в определенном интеграле
- •7.4 Вопросы для самопроверки
- •7.5 Вопросы для самостоятельной работы
- •Лекция №8
- •8.1 Вычисление площадей плоских фигур
- •8.2 Нахождение объемов тел вращения
- •8.3 Несобственные интегралы
- •I) Несобственные интегралы с бесконечными пределами интегрирования
- •II) Несобственные интегралы от разрывных функций.
- •8.4 Вопросы для самопроверки
- •Лекция 9
- •9.1 Основная идея численных методов вычисления приближенного
- •9.2 Метод прямоугольников
- •9.3 Метод трапеций
- •9.4 Метод Симпсона
- •9.5 Вопросы для самопроверки
- •9.6 Вопросы для самостоятельной работы
- •Лекция 10
- •10.1 Задачи, приводящие к дифференциальным уравнениям
- •10.2 Дифференциальные уравнения первого порядка:
- •10.3 Дифференциальные уравнения с разделенными переменными
- •10.4 Дифференциальные уравнения с разделяющимися
- •10.5 Вопросы для самопроверки
- •10.6 Вопросы для самостоятельной работы
- •Лекция 11
- •11.1 Линейные дифференциальные уравнения 1-го порядка.
- •11.5 Вопросы для самопроверки
- •Лекция № 12
- •12.1 Линейные дифференциальные уравнения второго порядка
- •12.2 Однородные линейные дифференциальные уравнения второго
- •Понятие о комплексных числах
- •12.3 Вопросы для самопроверки
- •12.4 Вопросы для самостоятельной работы
- •Лекция №13
- •13.1 Нахождение общего решения нлу 2-го порядка
- •13.2 Метод подбора частного решения нлу в случае, когда правая
- •13.3 Метод подбора частного решения нлу в случае, когда правая
- •13.4 Теорема о наложении решений
- •13.5 Вопросы для самопроверки
- •13.6 Вопросы для самостоятельной работы
- •Лекция №14
- •14.1 Определение числового ряда и его сходимости
- •14.2 Свойства сходящихся рядов
- •14.3 Необходимый признак сходимости и его следствие
- •14.4 Вопросы для самопроверки
- •14.5 Вопросы для самостоятельной работы
- •Лекция №15
- •15.1 Достаточные признаки сходимости рядов с положительными
- •15.2 Знакопеременные ряды. Достаточный признак сходимости
- •15.3 Знакочередующиеся ряды. Признак Лейбница
- •15.4 Функциональные ряды. Область сходимости степенного ряда
- •15.5 Степенные ряды. Нахождение области сходимости степенного
- •15.6 Вопросы для самопроверки
- •15.7 Вопросы для самостоятельной работы
- •Лекция №16
- •16.1 Разложение функций в степенные ряды
- •16.2 Ряды Тейлора и Маклорена
- •16.3 Разложение некоторых элементарных функций в ряд
- •16.4 Применение рядов к приближенным вычислениям
- •16.5 Вопросы для самопроверки
- •16.6 Вопросы для самостоятельной работы
- •Рекомендуемая литература
- •Функции нескольких переменных. Интегральное исчисление. Дифференциальные уравнения. Ряды
- •080502 – „Экономика и управление на предприятии”
- •080507 – „Менеджмент организации”
- •050501.18 – „Профессиональное обучение (экономика и управление)”
1.3 Предел и непрерывность функции
Большая часть основных понятий математического анализа, определенных ранее для функций одной переменной, может быть перенесена на случай функции двух переменных.
О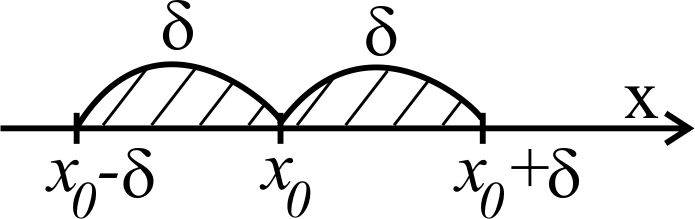 днако
несмотря на общность понятий, естественно,
что в соответствующих определениях
будут и отличия. Так в определении
предела функции одной переменной
вводилось понятие
днако
несмотря на общность понятий, естественно,
что в соответствующих определениях
будут и отличия. Так в определении
предела функции одной переменной
вводилось понятие
![]() -окрестности
точки
-окрестности
точки
![]() ,
под которой понимался
симметричный интервал относительно
и радиуса
(рисунок 4) (
,
под которой понимался
симметричный интервал относительно
и радиуса
(рисунок 4) (![]() ).
Если мы выбирали произвольную
).
Если мы выбирали произвольную
точку x из этой окрестности, то расстояние от неё
до
было меньше
,
т.е.
![]() или
или
![]() .
.
Для функции двух переменных введем понятия Рисунок 4
расстояния
и
-окрестности
точки
![]() .
.
О пределение.
Расстоянием
от точки
пределение.
Расстоянием
от точки
![]() до точки
до точки
![]() называется число
называется число
![]() ,
равное
,
равное
![]() .
(1.3)
.
(1.3)
О
![]() таких, что
таких, что
![]() .
.
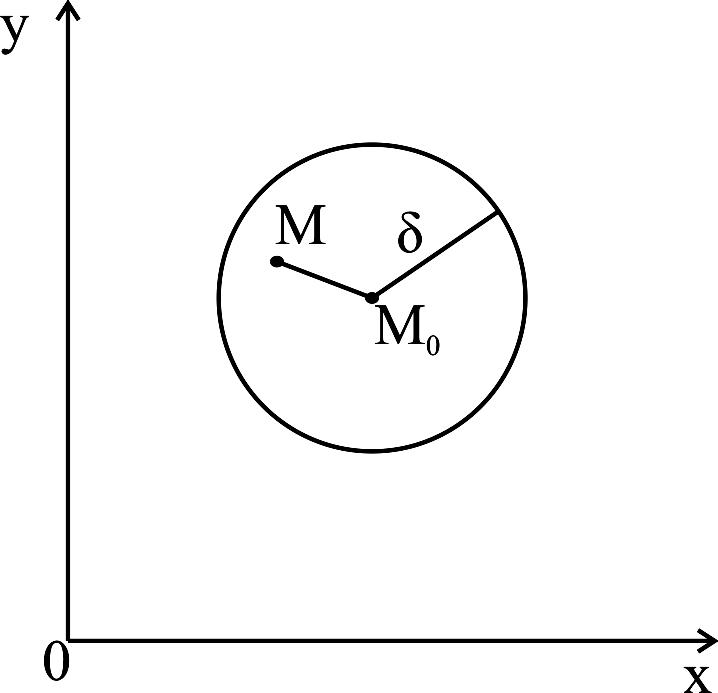
Из этого определения и определения
окружности следует, что геометрически
δ-окрестность
точки
![]() - это все
- это все
внутренние точки круга с центром
и радиусом δ (рисунок 5).
О пределение.
Число а
называется пределом
пределение.
Число а
называется пределом
функции
при
![]() ,
,
![]() (или в
(или в
точке
![]() ),
если для любого, даже сколь Рисунок 5
),
если для любого, даже сколь Рисунок 5
угодно
малого положительного числа
![]() ,
найдется положительное число
,
найдется положительное число
![]() ,
зависящее от
,
зависящее от
![]() ,
такое, что для всех точек
,
отстоящих от точки
на расстояние
меньшее, чем
,
такое, что для всех точек
,
отстоящих от точки
на расстояние
меньшее, чем
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Краткая запись:
![]()
![]() . (1.4)
. (1.4)
Из определения следует, что если предел существует, то он не зависит от пути, по которому точка стремится к точке .
Практически все теоремы о пределах, справедливые для функции одной переменной, выполняются и для функции .
Пример 1.3
Найти пределы функций:
а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение.
а)
Чтобы вычислить предел необходимо
подставить предельные значения аргументов
![]() и
и
![]() в функцию, т.е.
в функцию, т.е.
![]() .
Следовательно,
.
Следовательно,
![]() .
.
б)
Подстановка предельных значений
аргументов
![]() и
и
![]() приводит к неопределенности вида
приводит к неопределенности вида
![]() .
Чтобы её раскрыть, сведем функцию двух
переменных к функции одной переменной,
введя замену
.
Чтобы её раскрыть, сведем функцию двух
переменных к функции одной переменной,
введя замену
![]() .
.
Условие
![]() равносильно тому, что
равносильно тому, что
![]() .
Тогда получаем:
.
Тогда получаем:
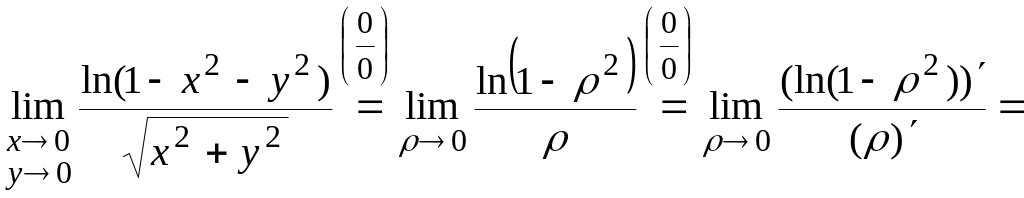
 .
При раскрытии
неопределенности
использовалось правило Лопиталя.
.
При раскрытии
неопределенности
использовалось правило Лопиталя.
Как видно из данного примера, вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной.
Причина заключается в том, что на прямой существуют только два направления, по которым аргумент может стремиться к предельной точке (справа или слева). На плоскости же таких направлений - бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
в)
В данном примере также имеем неопределенность
вида
![]() .
Будем приближаться к точке О (0; 0) по
прямым
.
Будем приближаться к точке О (0; 0) по
прямым
![]() .
Если
,
то
.
Если
,
то
 ,
,
где k – некоторое число.
Получим, что значение предела зависит от углового коэффициента прямой. Так как предел функции не должен зависеть от способа приближения точки (x; y) к точке (0; 0), то рассматриваемый предел не существует.
Аналогично понятию
непрерывности для функции
![]() вводится непрерывность и для функции
.
вводится непрерывность и для функции
.
 Определение.
Функция
называется непрерывной
в точке
Определение.
Функция
называется непрерывной
в точке
![]() ,
если ее предел в этой точке совпадет со
значением
,
если ее предел в этой точке совпадет со
значением
функции в данной точке, то есть
непрерывна в точке
![]() (1.5)
(1.5)
Данное определение в подробной записи выглядит так:
непрерывна в точке (x0, y0), если выполняются условия:
а)
![]() ;
;
б)
![]() - конечный;
- конечный;
в)
![]() .
.
Г еометрический смысл непрерывности очевиден: график функции в точке (x0, y0), представляет собой нерасслаивающую поверхность.
Определение. Будем говорить, что функция непрерывна на
множестве, если она непрерывна в каждой точке этого множества.
Определение. Точки, в которых нарушается непрерывность, называются
 точками
разрыва
функции.
точками
разрыва
функции.
В отличие от функции одной переменной точки разрыва могут образовывать целые линии разрыва.
Например,
функция
![]() имеет линию разрыва
имеет линию разрыва
![]() ,
то как в точках этой линии дробь, задающая
функцию, не существует (знаменатель
равен нулю).
,
то как в точках этой линии дробь, задающая
функцию, не существует (знаменатель
равен нулю).
