8.2 Нахождение объемов тел вращения

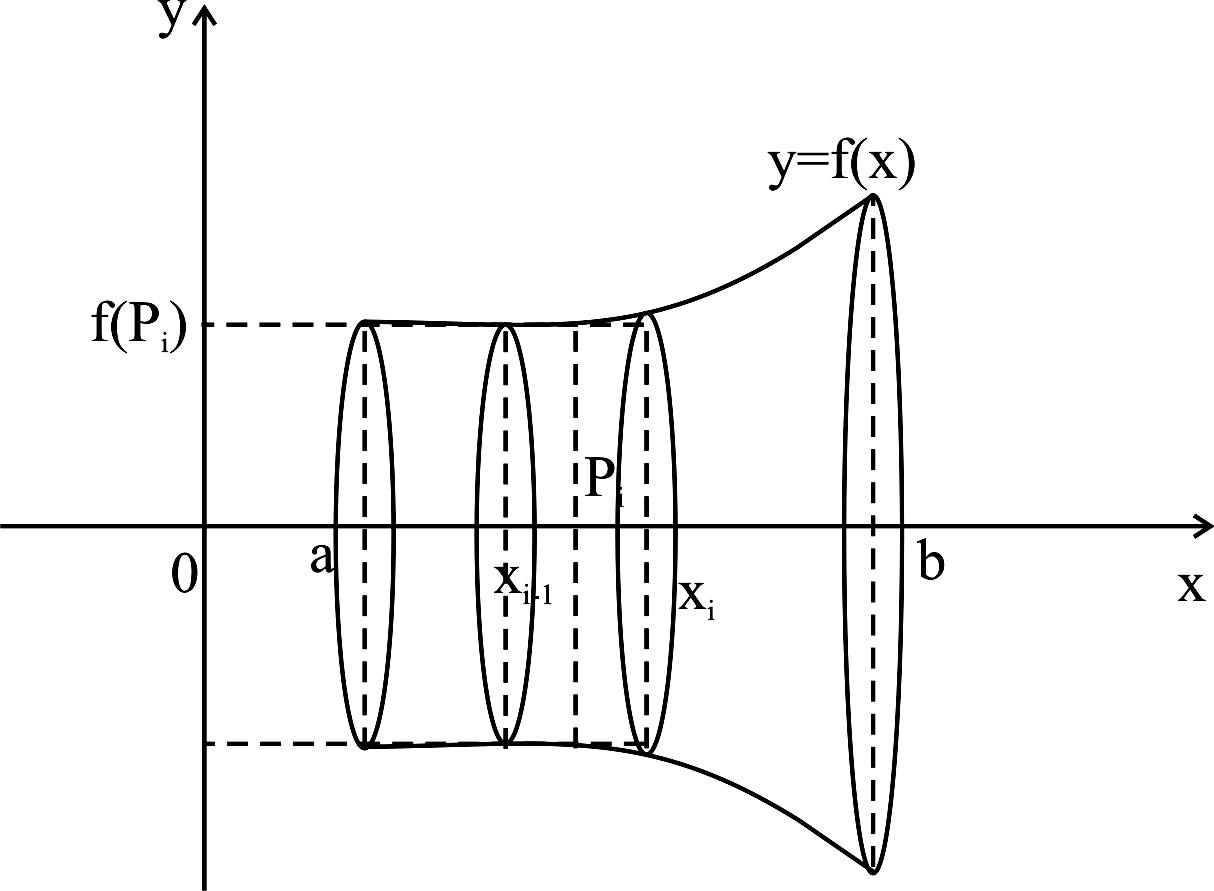
Пусть на отрезке [a, b] задана непрерывная неотрицательная функция . Необходимо найти объем V_ox тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями , (рисунок 26).

Для решения задачи применяем тот

же подход, который был использована

для нахождения площади криволиней-

ной трапеции. Разобьем отрезок [a, b]

произвольным образом точками

< < <…< на n

частичных отрезков ,

на каждом из которых некоторым

образом выберем точку и

найдем значение функции в ней . Рисунок 26

Заменим объем тела вращения на сумму объемов «узких» цилиндров, полученных при вращении соответствующих прямоугольников с высотой, равной и шириной, раной длине частичного отрезка . Так как при вращении прямоугольника вокруг оси OX каждая его точка описывает окружность, то объем каждого из этих цилиндров равен произведению площади основания на высоту , то есть . Сумма объемов всех «узких» цилиндров составит: ;

и

она дает приближенное значение объема

V_ox рассматриваемого тела вращения.

Точное значение V_ox получится как предел

таких сумм при , где

, то есть:

.

Тогда по определению определенного

интеграла получаем:

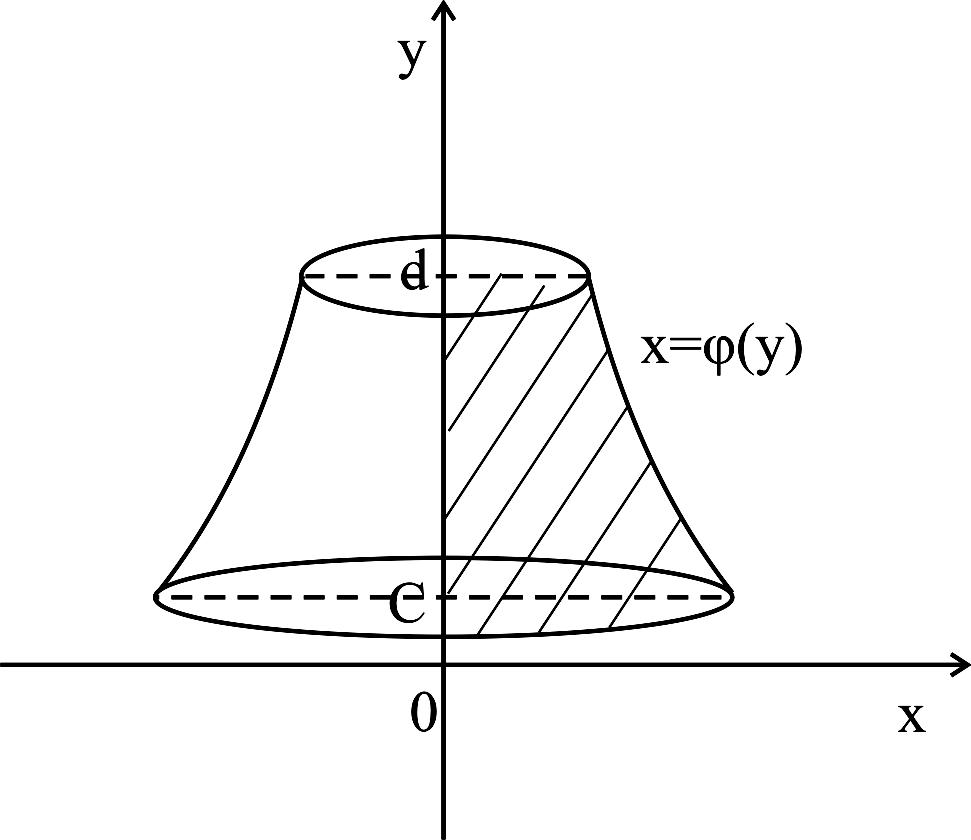
Рисунок 27

(8.8)

Формально заменяя в формуле (8.8) переменную x на y, получаем формулу для вычисления объема V_OY тела, полученного от вращения криволинейной трапеции (рисунок 27) вокруг оси ординат:

(8.9)

Если вокруг оси OX вращается не

криволинейная трапеция, а область, огра-

ниченная линиями ,

причем , (рису-

нок 28), то объем получившегося тела

вращения определяется по формуле:

(8.10) Рисунок 28

П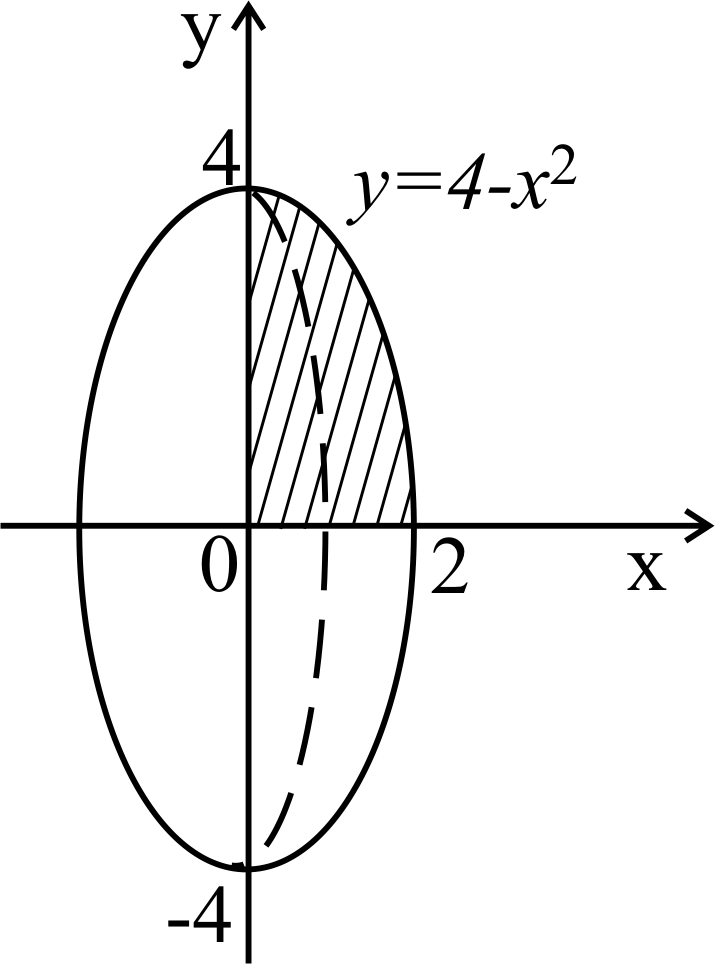 ример 8.2 Найти объемы тел, образованных

вращением вокруг осей OX и OY фигуры, огра-

ниченной линиями: , где .

Решение. а) Рассмотрим тело, которое образовано

вращением вокруг оси абсцисс заданной фигуры

(рисунок 29). Тогда объем этого тела определяется

по формуле (8.8): , где [a, b] –

отрезок оси OX, в который проектируется фигура.

В нашем случае a = 0, b = 2, а . Рисунок 29

Следовательно, объем тела вращения равен:

(куб. ед.).

б) Теперь рассмотрим случай вращения заданной фигуры вокруг оси OY (рисунок 30). Объем полученного тела вращения вычисляется по формуле (8.9): . Здесь отрезок [c, d] оси OY, в который проектируется криволинейная трапеция. В данном примере .

П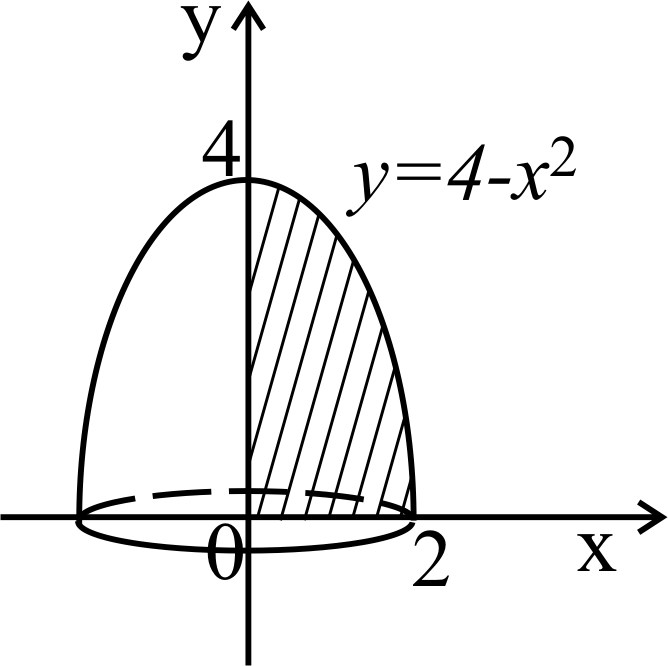 од интегралом находится квадрат

функции . Выразим из уравнения

параболы и подставим в интеграл:

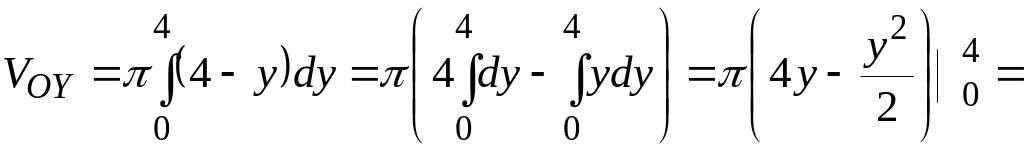
(куб. ед.). Рисунок 30

8.3 Несобственные интегралы

Рассматривая определение определенного интеграла, мы считали, что функция f(x) задана на отрезке [a, b] и непрерывна на нем. На практике возникает необходимость обобщения понятия интеграла на случаи, когда либо один из концов (или оба) отрезка интегрирования удален в бесконечность, либо функция разрывна на отрезке интегрирования.