7.4 Вопросы для самопроверки

1. Какая из указанных ниже формул является формулой Ньютона –

Лейбница: а) ; б) ;

в) ?

2. Как выглядит формула интегрирования по частям в определенном интеграле? В чем ее отличие от соответствующей формулы для неопределенного интеграла?

3. Как осуществляется замена переменной в определенном интеграле? В чем ее отличие от замены переменной в неопределенном интеграле?

4. Для каких видов интегралов следует применять: а) метод интегрирования по частям; б) метод замены переменной?

7.5 Вопросы для самостоятельной работы

С помощью рекомендуемой литературы [1, 3] изучите и законспектируйте дальнейшие свойства определенного интеграла.

Лекция №8

Тема: Геометрические приложения

определенного интеграла

8.1 Вычисление площадей плоских фигур

8.2 Нахождение объемов тел вращения

8.3 Несобственные интегралы

8.4 Вопросы для самопроверки

8.1 Вычисление площадей плоских фигур

а) Пусть функция непрерывна и

неотрицательна на отрезке [a, b]. Тогда на

основании геометрического смысла определенного

интеграла площадь S соответствующей криволиней-

ной трапеции (рисунок 12) численно равна опреде-

ленному интегралу , то есть, если

н а [a, b], то: Рисунок 12

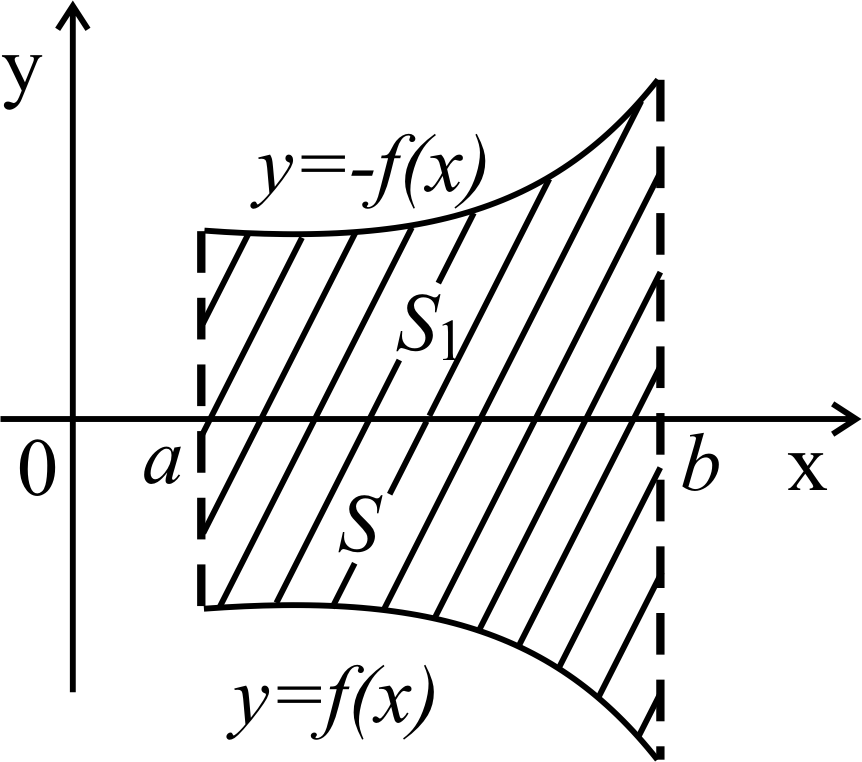
(8.1)

б) Пусть функция непрерывна и

неположительна на отрезке [a, b] (рисунок 13).

Требуется найти площадь заштрихованной

области S. Отражая кривую симметрично

относительно оси абсцисс, получим кривую с

уравнением .

Функция уже неотрицательна

на [a, b], а площадь S₁ под этой кривой на [a, b] Рисунок 13

из соображения симметрии равна площади S. На основании формулы (8.1) тогда можно записать: .

Таким образом, если на [a, b], то:

(8.2)

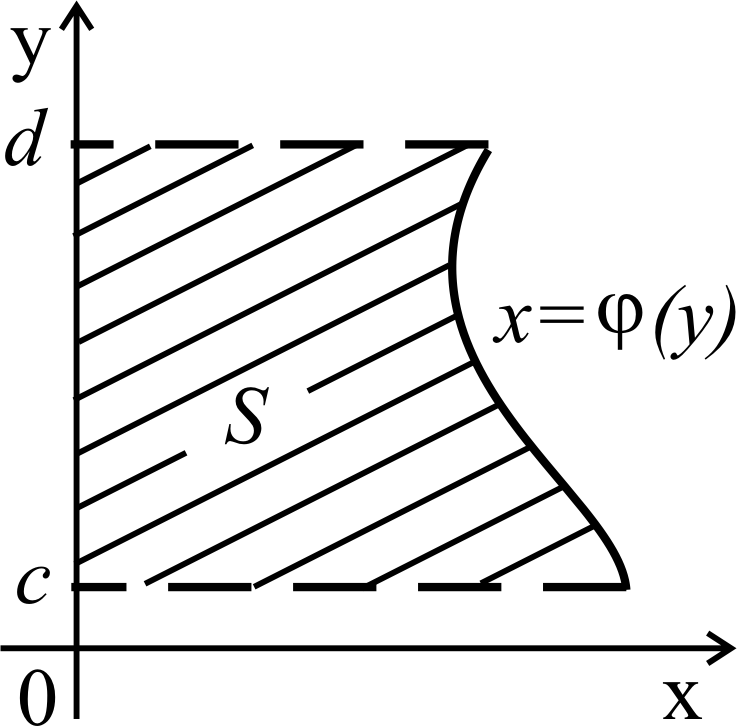в) Если криволинейная трапеция ограничена

непрерывной и неотрицательной на отрезке [c, d]

функцией (рисунок 14), то на основании

геометрического смысла определенного интеграла,

ее площадь S равна:

(8.3)

г) Пусть на отрезке [a, b] задана Рисунок 14

н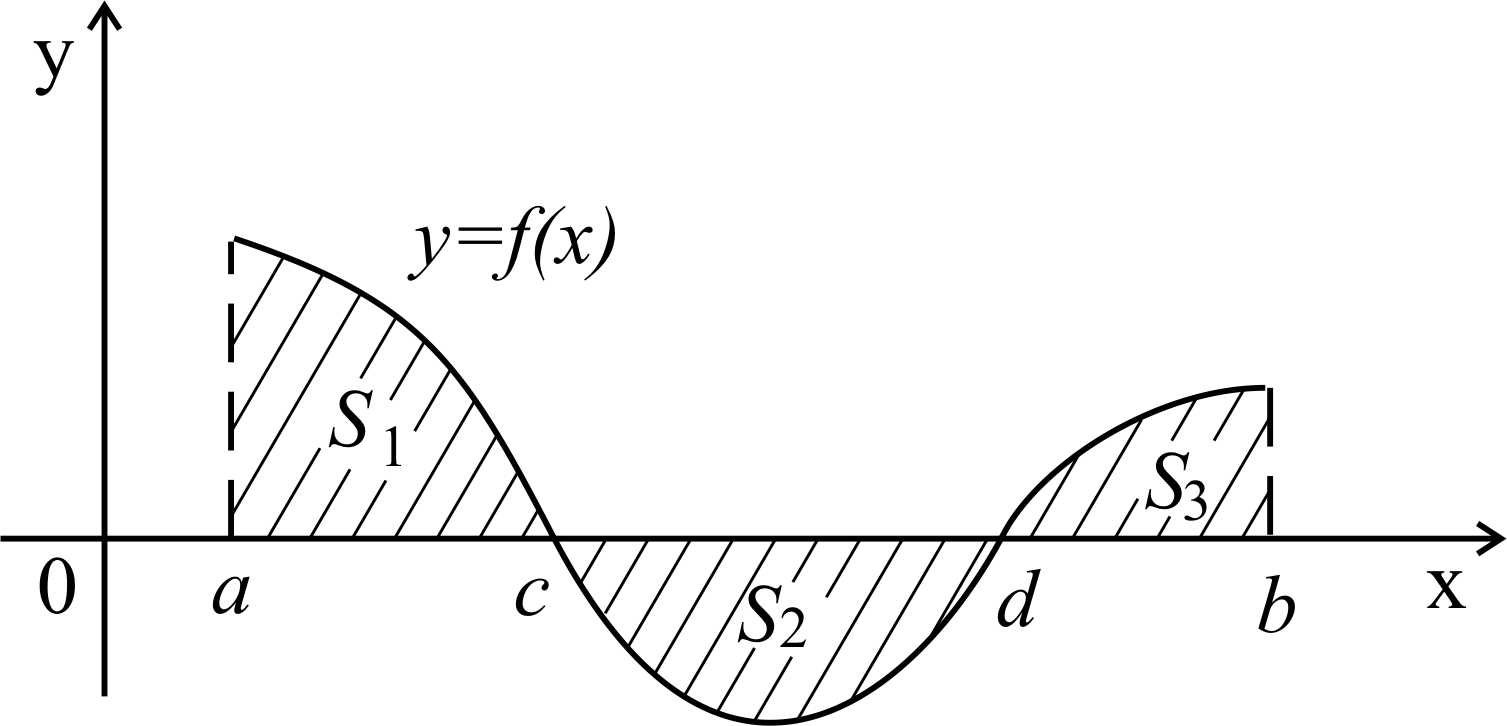 епрерывная

функция общего вида,

когда исходный отрезок можно

разбить точками на конечное

число интервалов так, что на

каждом из них функция

будет знакопостоянна или равна

нулю (рисунок 15).

В этом случае площадь S заштри- Рисунок 15

хованной фигуры будет равна: , или, с учетом а), б):

(8.4)

д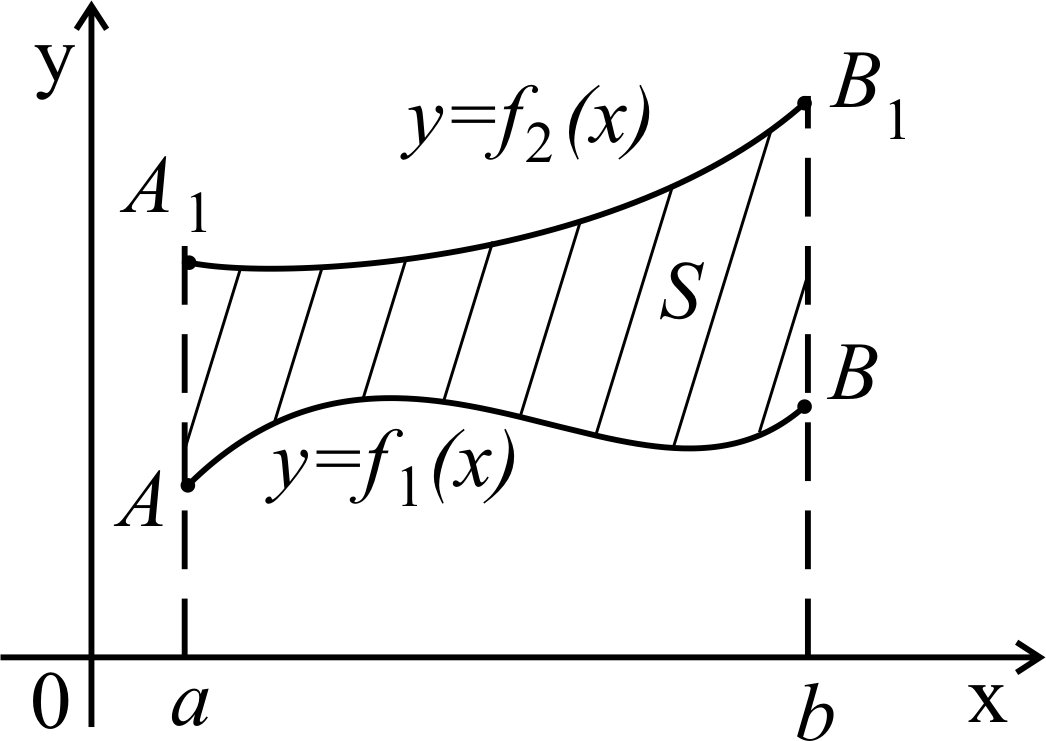 ) Пусть заданы две непрерывные и

неотрицательные функции ,

на отрезке [a, b], причем ,

(рисунок 16). Тогда площадь S заштрихованной

области может быть определена как разность

соответствующих криволинейных трапеций:

. Рисунок 16

Используя свойства определенного интеграла, получаем:

(8.5)

Можно показать, что формула (8.5) справедлива при любых расположениях кривых и с сохранением соотношения , для любых (рисунки 17, 18, 19).

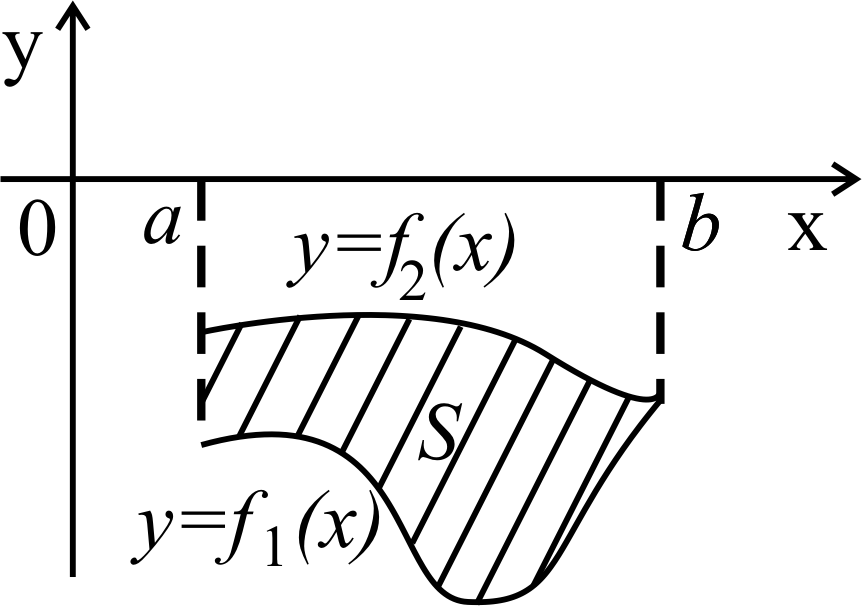
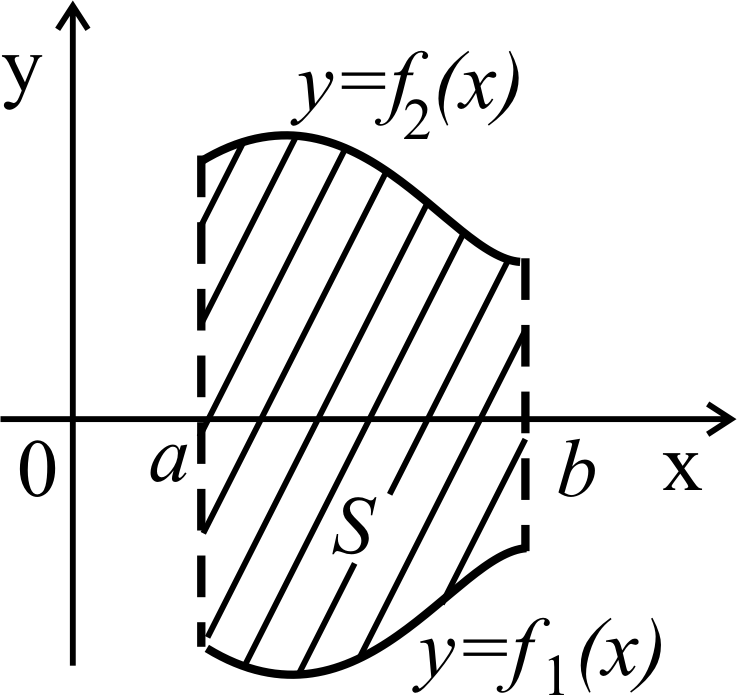
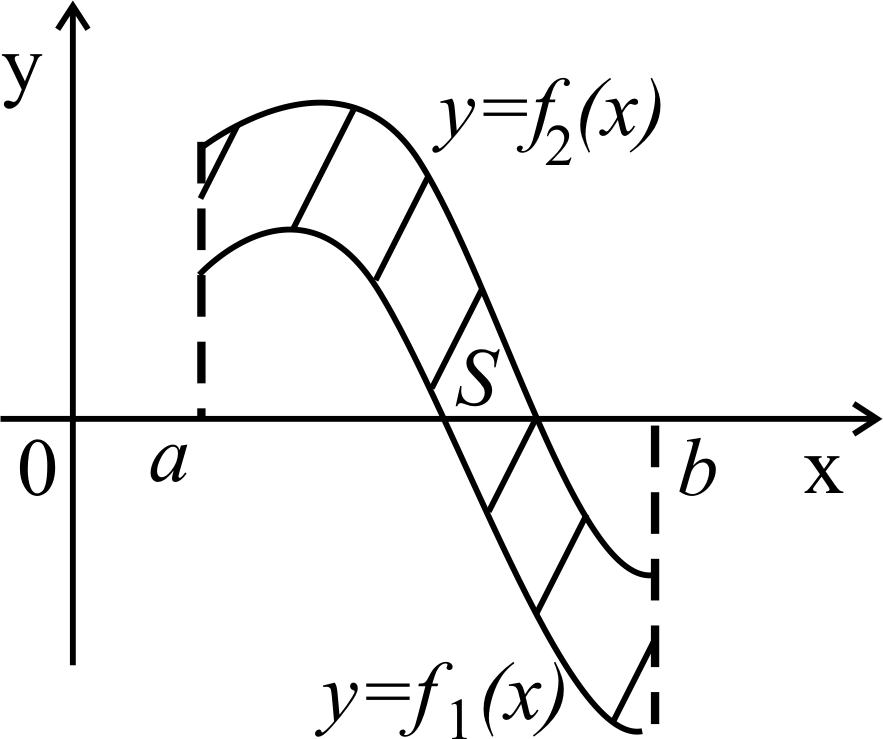
Рисунок 17 Рисунок 18 Рисунок 19

e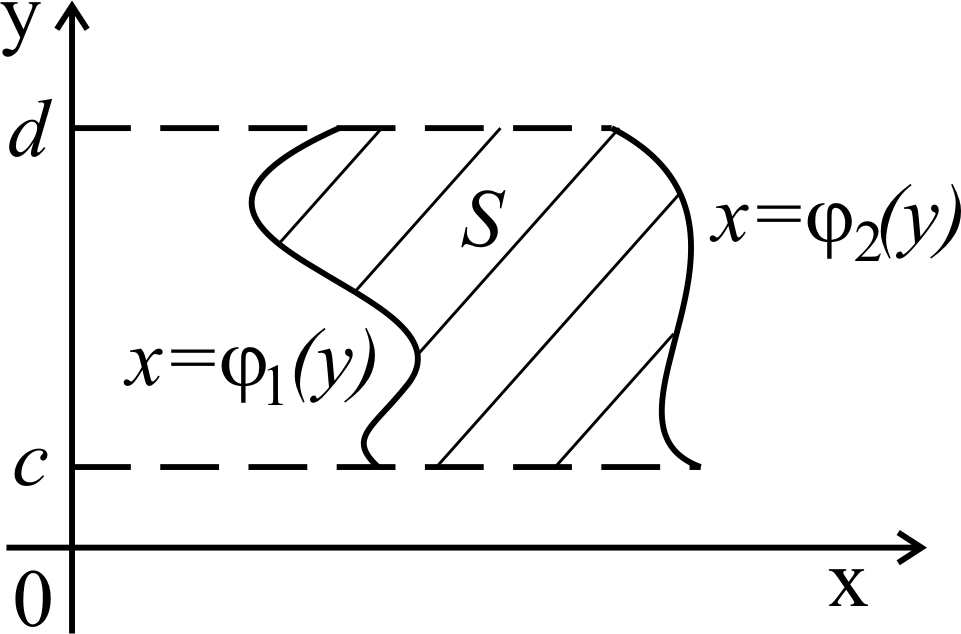 ) пусть заданы две непрерывные и

неотрицательные функции ,

на отрезке [c, d], причем

, (рисунок 20).

Тогда площадь S заштрихованной области

определяется по аналогии с пунктом д)

по формуле: Рисунок 20

, (8.6)

причем она справедлива при любых расположениях кривых ,

с сохранением соотношения , для любых .

ж) Если кривая, ограничивающая криволинейную трапецию, задана двумя (или более) различными аналитичес-

к ими выражениями (рисунок 21), то необхо-

димо, опустив перпендикуляры на ось ОХ

(или OY) из точек перехода одного вида

кривой к другой, разбить фигуру на части

так, чтобы можно было применить к ним

уже известные формулы.

Так площадь S заштрихованной фигуры,

изображенной на рисунке 21, может быть

найдена следующим образом: Рисунок 21

(8.7)

Пример 8.1 Найти площадь фигуры, ограниченной линиями: а) , ; б) ; в) ;

г

) .

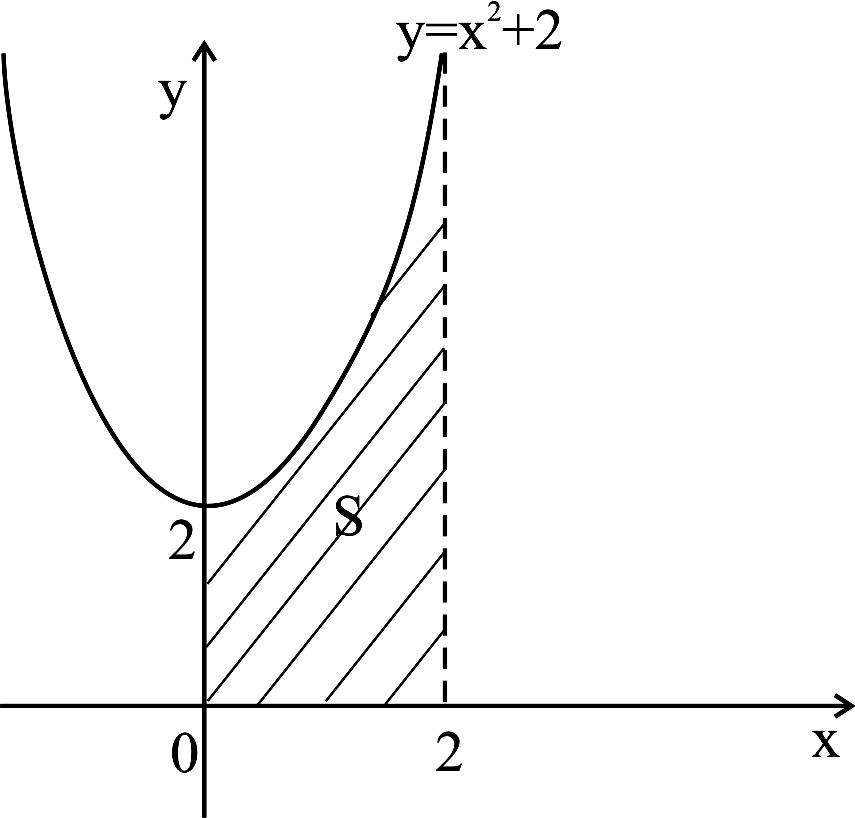
Решение. а) Построим область, площадь

которой необходимо найти. Линия, опреде-

ляемая уравнением представляет

собой параболу, ось симметрии которой –

ось OY, вершина находится в точке с коор-

динатами (0; 2), ветви направлены вверх

(рисунок 22). Слева и справа область огра-

ничена прямыми x = 0, x = 2, параллельными

оси OY, а снизу – осью OX (y = 0).

Полученная фигура представляет собой криво- Рисунок 22

линейную трапецию, площадь которой определяется по формуле (8.1): (кв. ед.).

б) Строим область: - парабола, ветви которой направлены вниз (ось

симметрии – OY), а - прямая, для построения которой берем точки

п

x	0	2
y	-2	0

ересечения с осями координат (рисунок 23).

Сверху – отрезок [0, 2] оси OX.

Заштрихованная область представляет собой

криволинейную трапецию, прилегающую

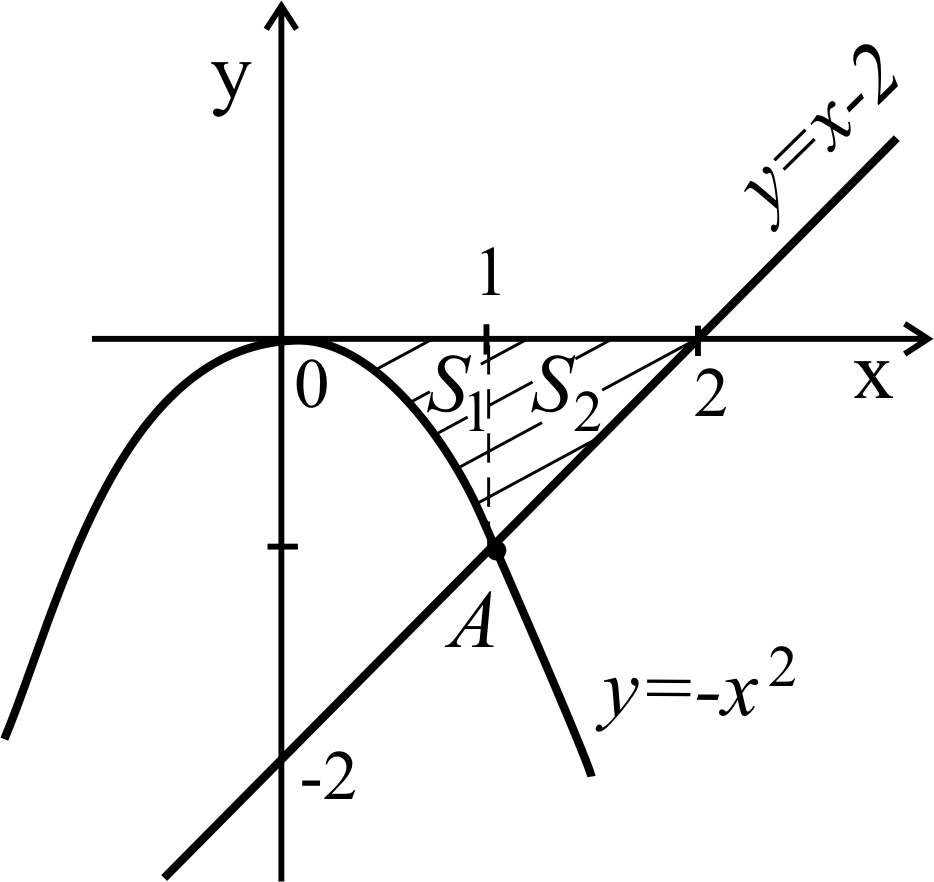« снизу» к отрезку [0, 2] оси OX, причем в

точке А происходит переход от параболы

к прямой. Поэтому для нахождения площади

всей области разобьем ее на части, проецируя

точку А на ось абсцисс. Найдем координаты

точки А как точки пересечения параболы и

прямой, решив систему из их уравнений:

Рисунок 23

Из рисунка видно, что точка А имеет координаты (1; -1). Следовательно, отрезок [0, 2] разбивается на две части: [0, 1] и [1, 2], на которых площади S₁ и S₂ криволинейных трапеций определяются по формуле (8.2), а площадь всей области S представляет их сумму:

(кв. ед.).

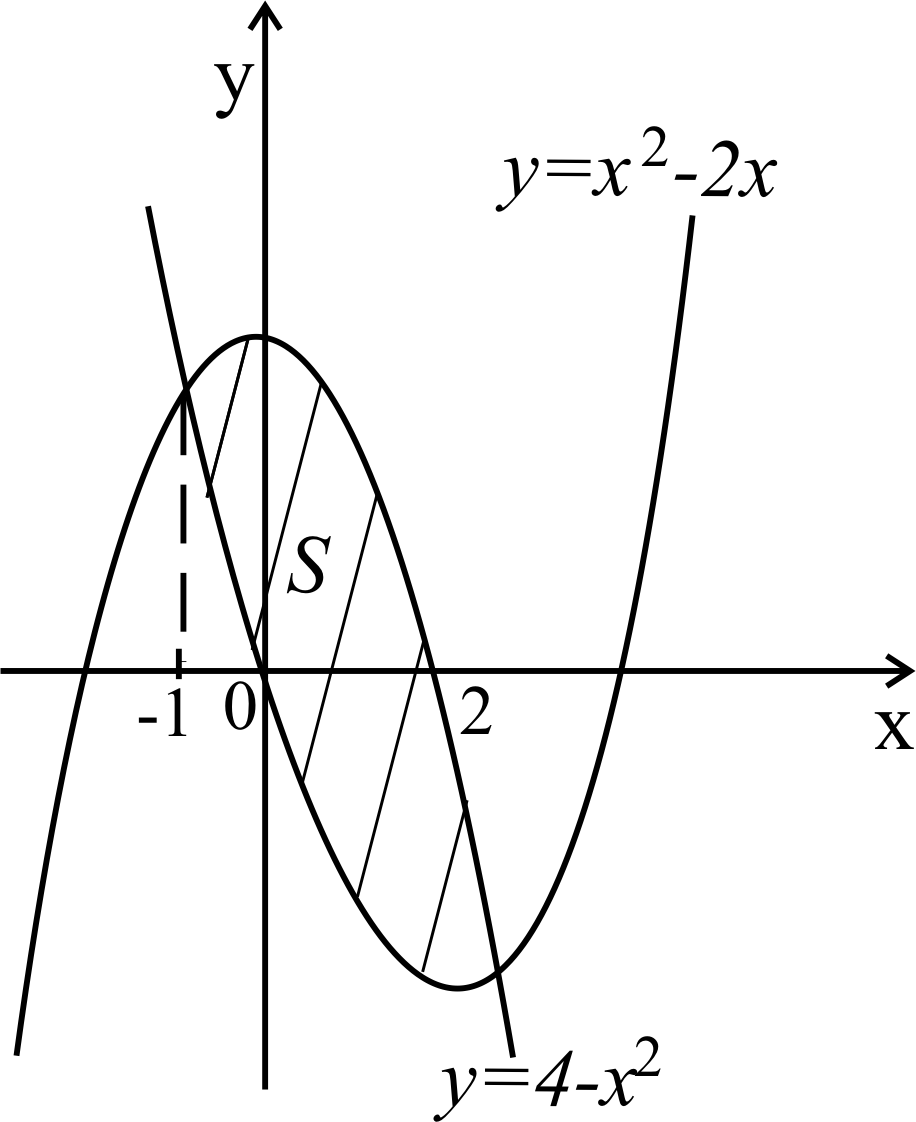
в) Обе кривые, ограничивающие фигуру –

параболы, строим их (рисунок 24).

Найдем точки пересечения заданных

кривых, решая систему из их уравнений:

Проецируя заштрихованную область на ось

абсцисс, мы видим, что на отрезке [-1; 2]

парабола находится все время выше,

чем парабола , то есть , Рисунок 24

. Применяя формулу (8.5), имеем:

(кв. ед.).

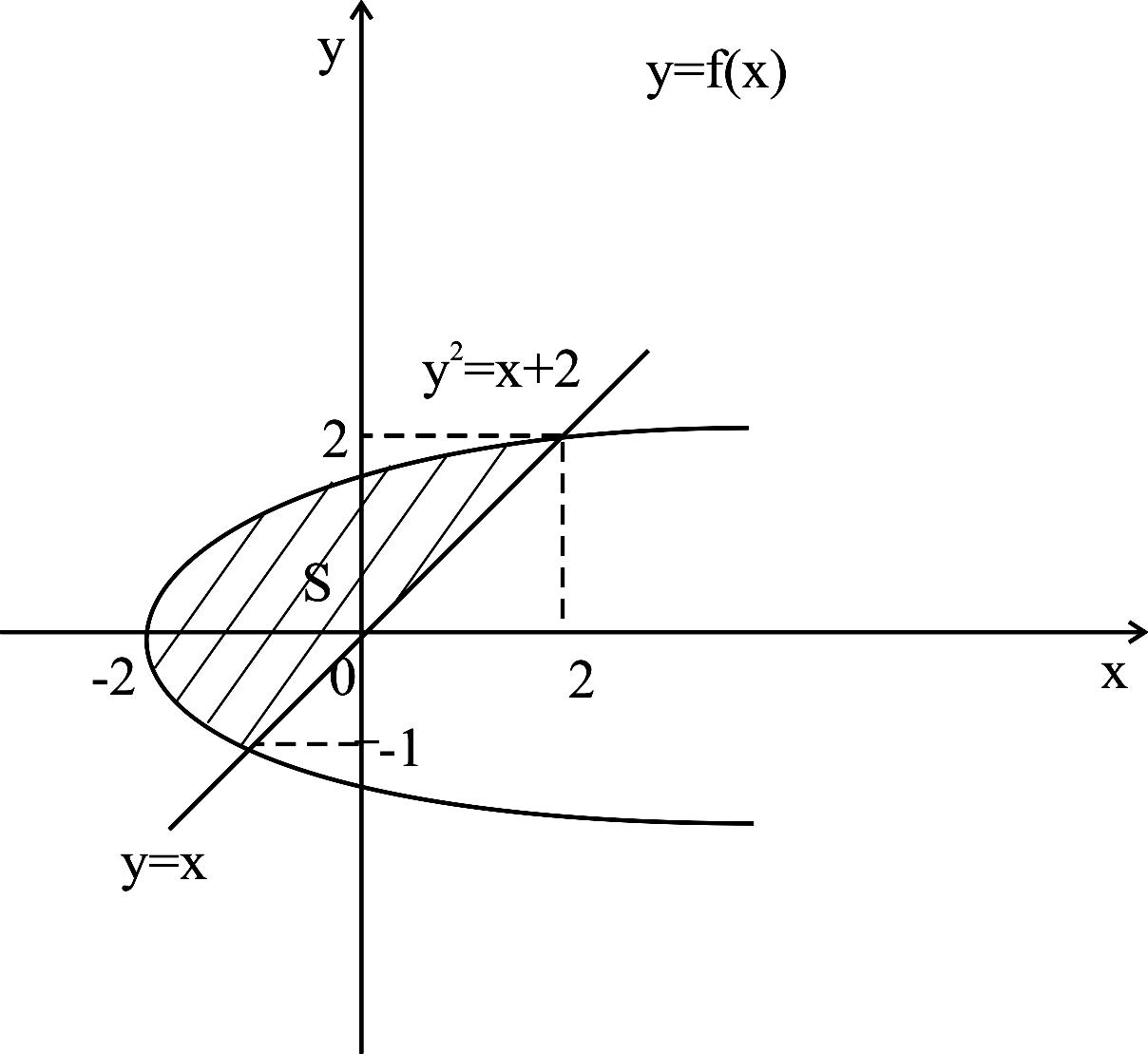
г) Кривая - парабола, ось симметрии которой – ось OX, ветви направлены вправо, а вершина имеет координаты (-2; 0). Прямая - биссектриса I и III координатных углов. Строим область, ограниченную заданными линиями (рисунок 25).

Найдем точки пересечения построенных линий:

Рисунок 25

Для нахождения искомой площади S удобнее проецировать область на ось ординат. Так как на отрезке [-1; 2] оси OY прямая находится «правее», чем парабола, то есть , , то применяем формулу (8.6):

(кв.ед).