5.4 Интегрирование некоторых видов иррациональностей

Рассмотрим некоторые типы интегралов, содержащих иррациональные выражения, которые с помощью подходящих замен переменных сведем к интегралам от рациональных функций.

Напомним, что рациональной функцией или рациональным выражением от переменных и называют частное от деления двух многочленов от и . Например, - рациональное выражение от и ; - рациональное выражение относительно и ; - рациональное выражение относительно и .

1 0. Интегралы от рациональных выражений, содержащих корни различных степеней из :

, (5.13)

сводятся к интегралам от рациональных дробей с помощью замены переменной

(5.14)

где - наименьшее общее кратное (НОК) показателей корней:

Пример 5.3 Вычислить интеграл .

Решение. Так как в подынтегральном рациональном выражении находятся корни различных степеней из , то необходимо от них избавиться и свести интеграл к рациональному выражению, не содержащему корней. Это легко сделать с помощью замены переменной (5.14), где Следовательно, положим , а далее будем выполнять необходимые этапы замены переменной:

Под знаком интеграла получилась рациональная дробь, которая может быть правильной, если степень многочлена, стоящего в числителе меньше, чем степень знаменателя. Если же степень числителя больше или равна степени знаменателя, то дробь называется неправильной. В данном случае дробь неправильная. У любой неправильной дроби, так же, как это было и в числах, можно выделить целую часть путем деления уголком многочлена, стоящего в числителе на многочлен, стоящий в знаменателе, или искусственно выделяя в числителе такое же выражение, что и в знаменателе. Это необходимо делать для сведения интеграла к табличным, которые содержат только правильные дроби.

В нашем случае покажем выделение целой части указанными двумя способами:

а) деление уголком:

б) искусственное выделение:

Следовательно,

20. Интегралы от рациональных выражений, содержащих корни различных степеней из :

(5.15)

сводятся к интегралам от рациональных дробей с помощью замены переменной:

, (5.16)

где

Пример 5.4 Вычислить интеграл .

Решение. Так как в подынтегральной функции содержится один корень, то введем замену , которая позволит избавиться от него:

.

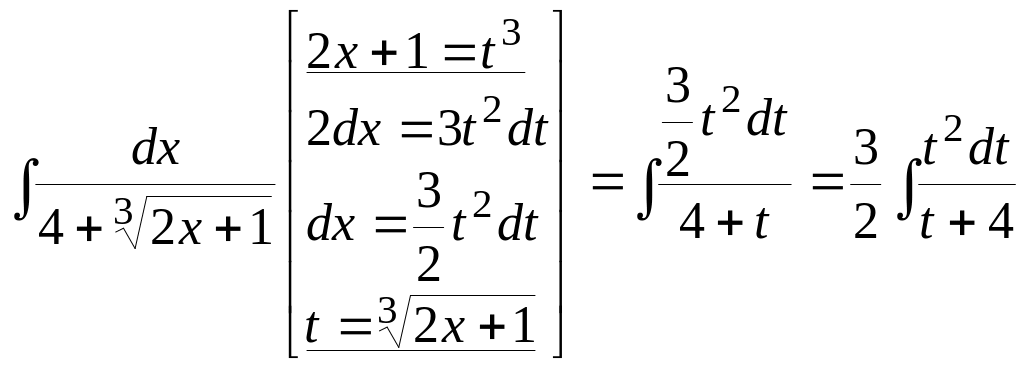У рациональной дроби , являющейся неправильной, выделим целую часть, поделив уголком:

Следовательно,

Тогда имеем:

5.5 Понятие о «неберущихся» интегралах

Из основных правил дифференцирования следовало, что производная произвольной элементарной функции вновь является функцией элементарной. Существенно, что операция нахождения первообразной, т.е. неопреде-

ленного интеграла, таким свойством не обладает, и существуют элементарные функции, у которых неопределенный интеграл не может быть выражен в элементарных функциях. Такие интегралы называются «неберущимися» в элементарных функциях, а сами функции – неинтегрируемыми в конечном виде.

Примерами таких интегралов служат

и т.д.

Для них не существует такой элементарной функции что и т.д.

Указанные «неберущиеся» интегралы не могут быть найдены с помощью основных методов интегрирования, однако это не означает, что указанные интегралы не существуют. Как правило, первообразные для этих интегралов хорошо изучены и для них составлены подробные таблицы, помогающие практически использовать эти функции. В дальнейшем мы познакомимся с методами вычислений значений таких функций.