5.2 Метод замены переменной

Во многих случаях удается введением вместо переменной интегрирования новой переменной свести данный интеграл к новому интегралу, который или содержится в таблице основных интегралов, или легко вычисляется другим способом. Этот метод интегрирования получил название метода замены переменной или метода интегрирования подстановкой.

Т еорема. Пусть в интеграле переменная заменяется некоторой функцией имеющей непрерывную производную, тогда справедлива следующая формула замены переменной:

. (5.7)

Доказательство. Для доказательства формулы (5.7), очевидно, достаточно убедиться, что дифференциалы обеих ее частей равны.

Дифференцируя левую часть соотношения (5.7), имеем:

Но так как , то . Поэтому

. (5.8)

С другой стороны, дифференцируя правую часть (5.7), имеем

. (5.9)

Соотношения (5.8) и (5.9) показывают, что

.

Тем самым справедливость формулы (5.7) доказана.

Допустим, что интеграл, стоящий в правой части соотношения (5.7), найден. Пусть .

Отсюда легко найти искомый интеграл в виде функции от . Для этого разрешим уравнение , относительно , т.е. найдем обратную функцию и подставим ее в :

. (5.10)

Анализ равенств в формуле (5.10) указывает на последовательность действий, которую необходимо выполнять при замене переменной.

Этапы замены переменной в неопределенном интеграле

1⁰. Необходимо выбрать подходящую замену переменной, например,

2⁰. Пересчитать дифференциал .

3⁰. Подставить и , найденные в п.1⁰, 2⁰, в подынтегральное выражение.

4⁰. С помощью алгебраических преобразований свести его к табличному (или сумме табличных) и найти соответствующую первообразную в зависимости от новой переменной .

5⁰. Вернуться к старой переменной , выразив из замены и подставив это значение в первообразную.

Замечание. Иногда целесообразно заменять не на функцию от , а функцию, зависящую от , на тогда

.

Успех интегрирования с помощью замены переменной зависит в значительной степени от того, сумеем ли мы подобрать такую подстановку, в результате которой данный интеграл будет сведен к табличному (или сумме табличных).

Рассмотрим применение метода замены переменной в некоторых частных случаях.

5.3 Интегрирование функций, содержащих квадратный трехчлен

К интегралам, содержащим квадратный трехчлен относятся интегралы вида:

(5.11)

где - некоторые числа, причем и одновременно не равны нулю.

Можно показать, что указанные интегралы будут сведены к табличным с помощью замены переменной:

(5.12)

Покажем это на примерах.

Пример 5.2 Вычислить интегралы: а) б) .

Решение. а) Так как подынтегральная функция содержит квадратный трехчлен , то по рекомендации (5.12) введем новую переменную , равную половине производной от этого трехчлена, а далее выполняем все этапы замены переменной:

Замечание. Пересчет квадратного трехчлена через новую переменную целесообразнее производить отдельно от интеграла, а затем полученный результат вернуть на свое место. При правильном раскрытии скобок обязательно члены, содержащие первую степень , взаимно уничтожатся.

б)

Пересчитаем квадратный трехчлен, стоящий в знаменателе через новую переменную t:

Получившиеся два интеграла сводятся к табличным:

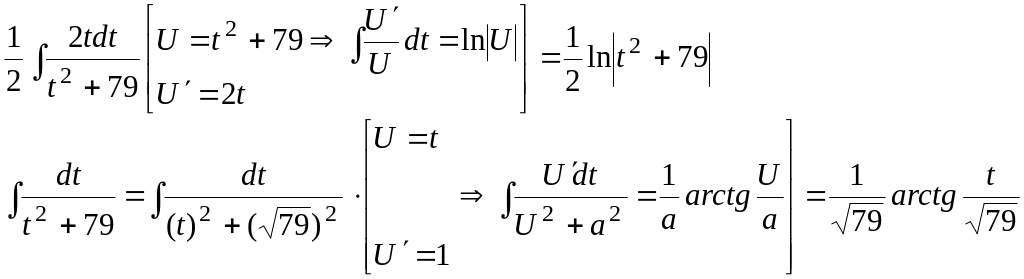
Тогда получаем:

.

Возвращаясь к старой переменной и заменяя получим окончательно