
- •Раздел 1: Эконометрические регрессионные модели и прогнозирование
- •Раздел 2: Расчетная часть 20
- •Введение
- •Раздел 1: Эконометрические регрессионные модели и прогнозирование на их основе
- •1.1. Эконометрика. Основные понятия и определения
- •1.2. Основные задачи эконометрических исследований
- •1.3. Модель множественной линейной регрессии
- •1.3.1 Построение модели множественной линейной регрессии с использованием метода наименьших квадратов (мнк)
- •1.3.2. Свойства оценок, полученных методом наименьших квадратов (мнк)
- •1.3.3. Анализ вариации зависимой переменной. Качество оценивания в модели множественной линейной регрессии
- •1.3.4. Прогнозирование с помощью регрессионных уравнений
- •Раздел 2: Расчетная часть
- •2.1. Постановка задачи распределения фондов минеральных удобрений сельскохозяйственного предприятия
- •Фонды удобрений планового периода и задания по производству продукции
- •Агрохимическая характеристика почв и план размещения сельскохозяйственных культур
- •«Стартовые» дозы удобрений (по видам) в зависимости от содержания в почве доступных форм p2 o5 и k2o
- •Характеристика удобрений и процессов их использования
- •Закупочные цены и удельные затраты на уборку и доработку 1 ц продукции
- •2.2. Разработка экономико-математической модели
- •2.2.1. Система переменных экономико-математической модели Участок №15
- •Участок №1
- •2.2.2 Система ограничений экономико-математической модели Группа ограничений по балансу выноса элементов питания продукций и внесения их с удобрениями
- •Группа ограничений по границе интервалов прибавки урожайности
- •Группа ограничений по формированию годовых норм удобрений в ассортименте поставки
- •Группа ограничений по распределению годовых норм удобрений по срокам внесения
- •Группа ограничений по допустимому удельному весу отдельных форм удобрений в общей дозе
- •Группа ограничений по суммарному приросту урожайности на участке
- •Группа ограничений по балансу ресурсов и потребления удобрений
- •Группа ограничений по производству продукции
- •2.2.3 Условия неотрицательности переменных экономико-математической модели
- •2.2.4 Целевая функция экономико-математической модели
- •2.3. Подготовка исходной информации
- •Расчет показателей последствия удобрений, внесенных под предшественники и плановых затрат удобрений, отнесенных на исходную урожайность
- •Расчет фондов удобрений, отнесенных на прирост урожая, т физ. Веса
- •Расчет показателя выхода продукции, отнесенной на исходную урожайность
- •Обеспечение заданных объемов производства продукции
- •2.4. Решение экономико-математической задачи распределения фондов минеральных удобрений сельскохозяйственной организации по полям севооборотов и кормовым угодьям
- •2.5 Формирование отчетов по результатам решения
- •Типы отчетов
- •2.6 Анализ результатов решения
- •Заключение
- •Список использованной литературы
1.3. Модель множественной линейной регрессии
1.3.1 Построение модели множественной линейной регрессии с использованием метода наименьших квадратов (мнк)
В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Простая регрессия
представляет
собой модель, где среднее значение
зависимой (объясняющей) переменной
 рассматривается как функция одной
независимой (объясняющей) переменной
рассматривается как функция одной
независимой (объясняющей) переменной
 ,
т.е. это модель вида
,
т.е. это модель вида
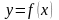 .
.
Множественная
регрессия представляет собой модель,
где среднее
значение зависимой (объясняющей)
переменной
рассматривается как функция нескольких
независимых (объясняющих) переменных
 ,
т.е. это модель вида
,
т.е. это модель вида
 .
.
Любой эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели исходя из соответствующей теории связи между явлениями.
В первую очередь из всего круга вопросов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки ― увеличивая объем исходных данных, то ошибки измерения практически могут свести на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.
Для
построения модели множественной линейной
регрессии с
 объясняющими переменными
зависимость
между ними в генеральной совокупности
представляется в виде:
объясняющими переменными
зависимость
между ними в генеральной совокупности
представляется в виде:
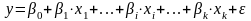 ,
,
где:
 объясняемая
– зависимая переменная;
объясняемая
– зависимая переменная;
 объясняющие
– независимые переменные;
объясняющие
– независимые переменные;
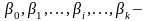 параметры
модели;
параметры
модели;
 случайное
слагаемое.
случайное
слагаемое.
Обычно при построении модели множественной линейной регрессии предполагается отсутствие корреляций всех объясняющих переменных друг с другом.
На основе
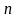 наблюдений получают выборочное уравнение
регрессии:
наблюдений получают выборочное уравнение
регрессии:
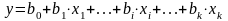 ,
,
где
 оценки параметров
оценки параметров
 .
.
Для оценки
параметров уравнения регрессии
используется метод наименьших квадратов
(МНК). Основные идеи МНК рассмотрим на
примере частного случая модели
множественной линейной регрессии при
 (т.е. модели
линейной парной регрессии):
(т.е. модели
линейной парной регрессии):
 .
.
При применении
МНК неизвестные оценки
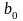 и
и
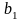 параметров уравнения регрессии определяют
путем минимизации суммы квадратов
остатков:
параметров уравнения регрессии определяют
путем минимизации суммы квадратов
остатков:

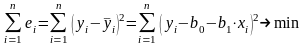 ,
,
где
 количество
пар переменных, используемых для анализа.
количество
пар переменных, используемых для анализа.
Необходимое условие минимума обеспечивается приравниванием нулю частных производных суммы квадратов остатков по величинам и :
 ,
,
 ,
,
где
 значок
дифференциала.
значок
дифференциала.
Из этих условий вытекают два уравнения для определения величин и :
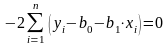 ,
,
 .
.
Решая систему из двух уравнений, получим:
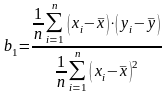 ,
,
 ,
,
где
 и
и
 выборочные средние значения переменных
и
.
выборочные средние значения переменных
и
.
Коэффициент
,
представляющий собой угловой коэффициент
регрессии, показывает скорость приращения
переменной
при изменении независимой переменной
и связан с коэффициентом корреляции
 величин
и
соотношением:
величин
и
соотношением:
 ,
,
где
 и
и
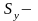 среднеквадратические
отклонения переменных
и
.
среднеквадратические
отклонения переменных
и
.
