Обеспечение заданных объемов производства продукции

Вариант	Задание по производству продукции, т
	Всего		из них
			Выполняется за счет исходного урожая		Подлежит выполнению за счет прироста урожая
	Ячмень	Озимая пшеница	Ячмень	Озимая пшеница	Ячмень	Озимая пшеница
15	277	277	73,8	132	203,2	145

2.4. Решение экономико-математической задачи распределения фондов минеральных удобрений сельскохозяйственной организации по полям севооборотов и кормовым угодьям

Разработанная экономико-математическая модель может быть решена симплексном методом, так как является задачей линейного программирования. Общий принцип, которых таков: выбирается неоптимальный опорный план и его параметры варьируются с целью последовательного улучшения плана, т.е. оптимизации целевой функции при соблюдении всех ограничений, что дает возможность решать оптимизационные задачи.

Рассмотренная задача решена с использованием приложения Поиск решения МS Excel.

Для решения задачи требуется внести в таблицу на рабочем листе МS Excel следующие данные (рис. 1,1а, 2,2а):

1) технико-экономические коэффициенты при переменных (по столбцам модели № 1...30):

а. переменные в столбцах модели № 1...15 отнесены к блоку участка №1;

b. переменные в столбцах модели № 16...30 - к участку № 2;

2) ограничения (по строкам модели № 1...34):

а. по участкам:

i. ограничения № 1...14 характеризуют участок № 1, в том числе по интервалам прибавки урожайности:

1. ограничения № 1…4 - по 1-му интервалу;

2. ограничения № 5...8 - по 2-му интервалу;

ii. ограничения № 15...28 характеризуют участок № 2, в том числе по интервалам прибавки урожайности:

1. ограничения № 15...18-по 1-ну интервалу;

2. ограничения № 19...22 - по 2-му интервалу;

b. по фондам удобрений: ограничения№ 29...32:

с. по объемам производства продукции: ограничения № 33, 34;

3) вводятся коэффициенты целевой функции при свободных переменных;

4) рассчитываются суммы значений по строкам;

5) вызов Данные - Поиск решения, далее - задать целевую ячейку (здесь АМ43), цель – «максимальное значение». Далее указывается массив изменяемых переменных и вводятся ограничения (рис. 3);

6) просмотр подменю Выберите метод решения, указывается Поиск решения линейных задач симплексным методом; запуск выполнения программы команда «Найти решение»;

7) появление измеренных значений переменных (рис. 4, строка 44) и значения целевой функции на экране (рис 4, АМ43).

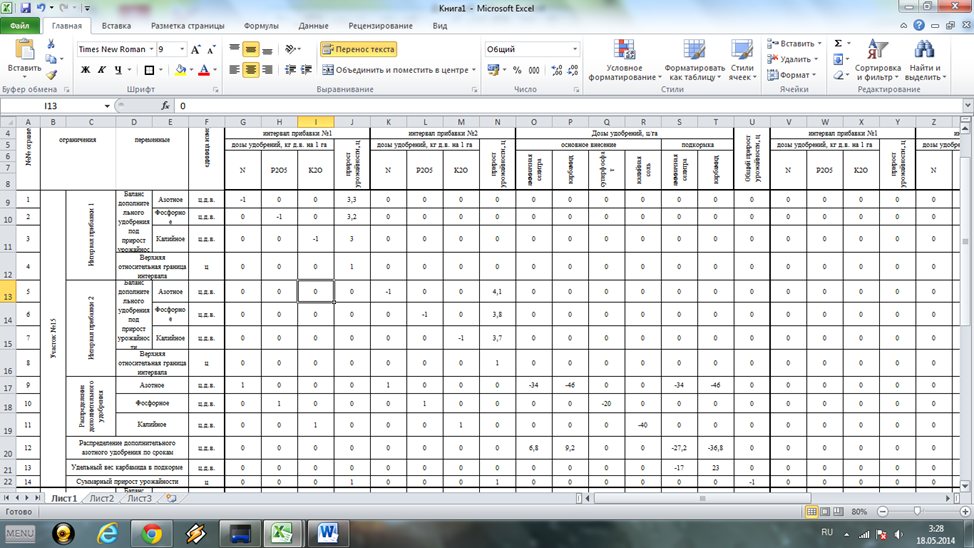
Рис. 1. Фрагмент рабочего листа MSExsel с исходными данными по участку №15

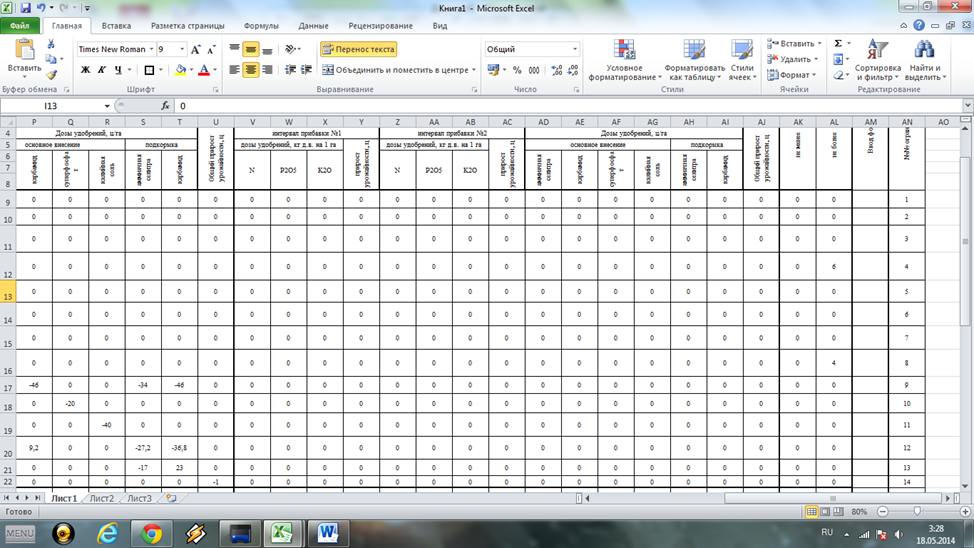
Рис. 1а. Фрагмент рабочего листа MSExsel с исходными данными по участку №15(продолжение)

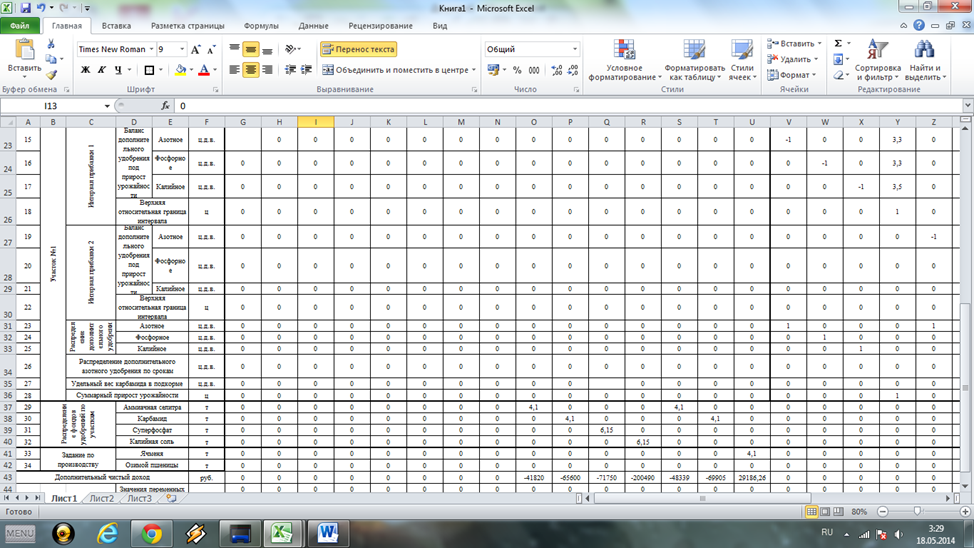
Рис.2. Фрагмент рабочего листа MSExsel с исходными данными по участку №1

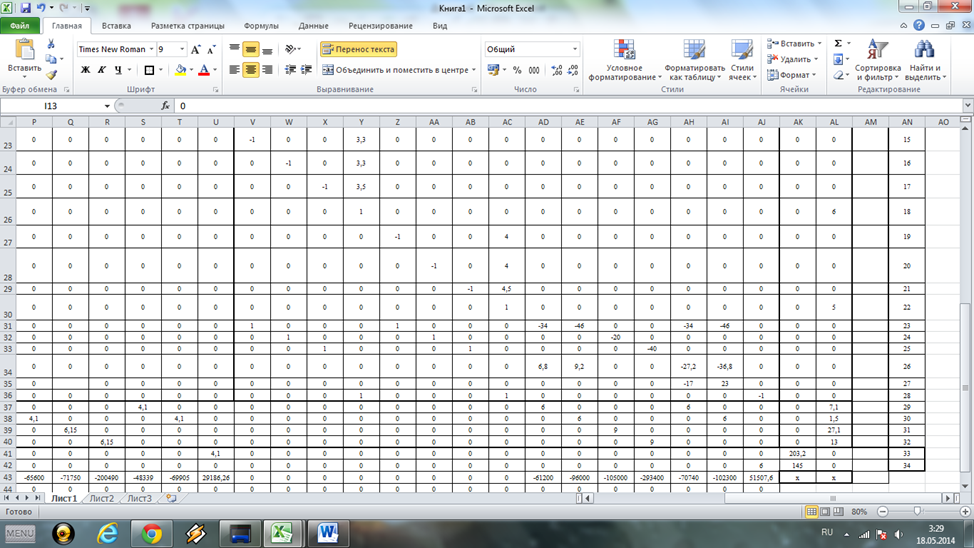
Рис. 2а. Фрагмент рабочего листа MSExsel с исходными данными по участку №1(продолжение)

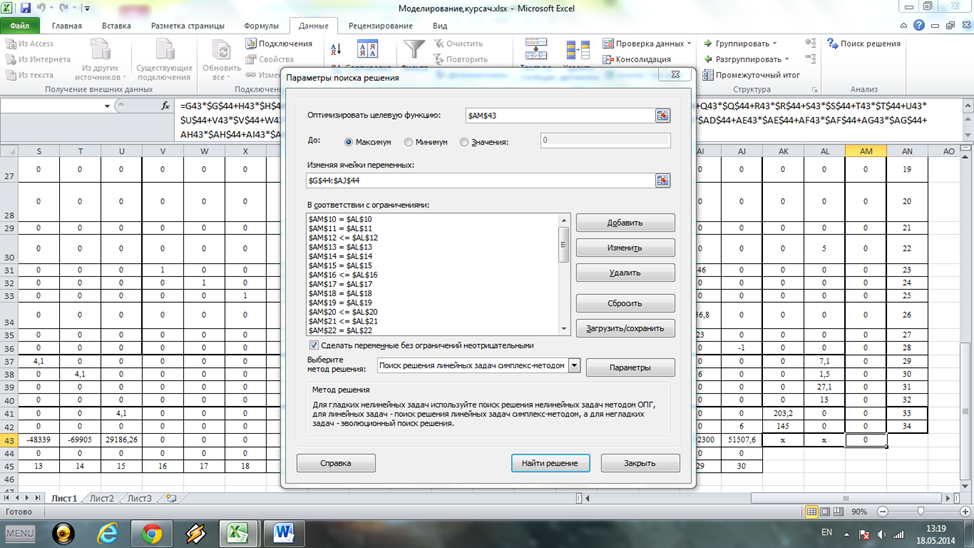
Рис. 3. Фрагмент диалогового окна Параметры Поиска решения

По результатам решения получены дозы внесения удобрений по различным культурам, в установленные сроки, приросты урожайности культур по интервалам внесения и общий прирост урожайности и величина дополнительного чистого дохода (см. рис. 4).

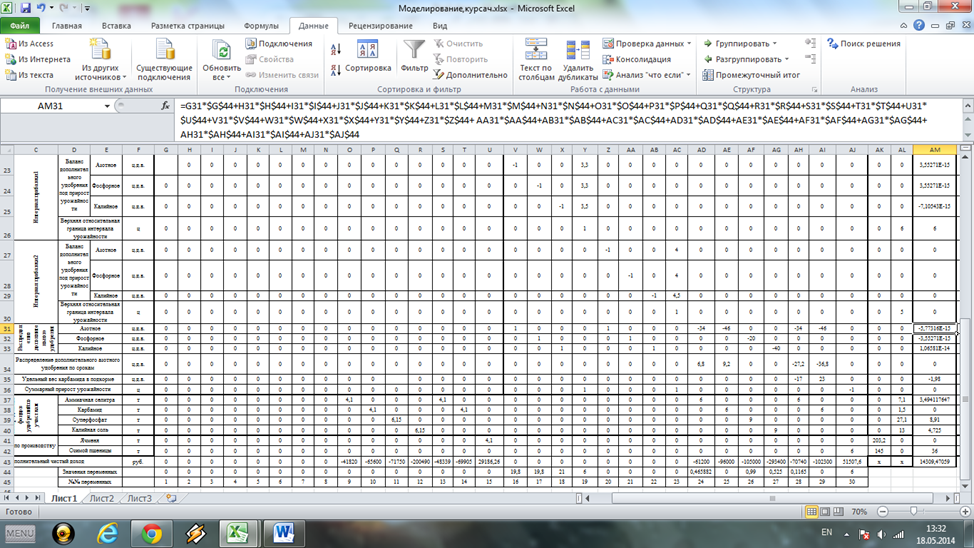
Рис. 4. План распределения фондов удобрений сельскохозяйственного предприятия по полям севооборотов и кормовым угодьям