Вставка в дереве бинарного поиска

Мы можем существенно упростить операцию вставки для пользователя дерева бинарного поиска: он должен предоставить только сам элемент. Пользователь не должен также беспокоиться о том, какой узел становится родительским, и в качестве какого дочернего узла добавляется новый узел. Все это, скрывая подробности, может выполнить дерево бинарного поиска, используя в качестве руководства к действию порядок элементов внутри дерева.

Фактически, вставить новый элемент в дерево бинарного поиска достаточно просто, и большая часть этого процесса уже была рассмотрена. Мы ищем элемент до тех пор, пока не достигаем точки, когда дальнейший спуск оказывается невозможен, поскольку дочерняя связь, которой нужно было бы следовать, является нулевой. К этому моменту мы знаем, где должен размещаться элемент, ‑ в точке, где мы должны были остановиться. При этом известно, каким дочерним узлом должен быть элемент, и, естественно, мы останавливаемся на родительском узле нового узла. Обратите также внимание, что используемый алгоритм поиска места для вставки нового элемента гарантирует целостность порядка элементов в дереве бинарного поиска.

Тем не менее, алгоритм вставки сопряжен с одной проблемой. Хотя метод гарантирует создание допустимого дерева бинарного поиска после выполнения операции, созданное дерево может быть неоптимальным или неэффективным. Чтобы понять, о чем идет речь, вставьте элементы a, b, c, d, e и f в пустое дерево бинарного поиска. С элементом а все просто ‑ он становится корневым узлом. Элемент b добавляется в качестве правого дочернего узла элемента a. Элемент c добавляется в качестве правого дочернего узла элемента b и т.д. Результат показан слева на рис. 8.2: он представляет собой длинное вытянутое дерево, которое можно трактовать как связного списка. В идеале желательно, чтобы дерево было более сбалансированным. Для только что созданного вырожденного дерева время поиска пропорционально числу элементов в дереве (О(n)), а не log(_2_) числа элементов (O(log(n))). Возможны также другие случаи вырождения. Например, попытайтесь выполнить следующую последовательность вставок: a, f, b, e, c и d, в результате которой создается явно вырожденное дерево, показанное справа на рис. 8.2.

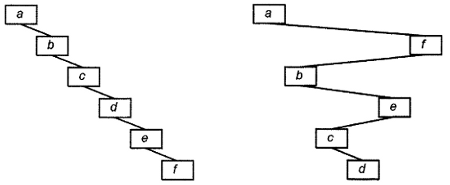
Рисунок 8.2. Вырожденные деревья бинарного поиска

В связи с возникновением описанных проблем, этот простой алгоритм вставки вряд ли будет применяться на практике. Если бы можно было гарантировать случайный порядок вставки ключей и элементов, или если бы общее количество элементов было очень небольшим, описанный алгоритм вставки оказался бы вполне приемлемым. Однако в общем случае подобную гарантию просто нельзя дать, и поэтому необходимо использовать более сложный алгоритм вставки, частью которого является попытка сбалансировать дерево бинарного поиска. Эта методика балансировки будет рассмотрена в ходе ознакомления с красно‑черными деревьями (RB‑деревьями).

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Важно иметь в виду следующее. Рассмотренные алгоритмы вставки и удаления гарантированно создают допустимое дерево бинарного поиска. Однако при этом весьма вероятно, что дерево будет скошенным и несбалансированным. Для небольших деревьев бинарного поиска это не имеет особого значения (в конце концов, для малых значений n log(n) и n ‑ величины более‑менее одного порядка, поэтому выигрыш в значении О большого будет небольшим), тем не менее, для больших деревьев такое различие поистине огромно.

‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑

Возвращаясь к простому алгоритму вставки, мы видим, что для вставки n элементов в дерево бинарного поиска в среднем требуется время, пропорциональное O(n log(n)) (другими словами, для каждой вставки используется алгоритм O(log(n)) для выяснения места, в которое должен быть помещен новый элемент, а количество вставляемых элементов равно n). В случае вырождения вставка n элементов превращается в операцию типа O(n(^2^)).

Листинг 8.14. Вставка в дерево бинарного поиска

function TtdBinarySearchTree.bstInsertPrim(aItem : pointer;

var aChildType : TtdChildType): PtdBinTreeNode;

begin

{вначале предпринять попытку найти элемент; если он найден, сгенерировать ошибку}

if bstFindItem(aItem, Result, aChildType) then

bstError(tdeBinTreeDupItem, 'bstInsertPrim');

{эта операция возвращает узел, поэтому вставку потребуется выполнить здесь}

Result := FBinTree.InsertAt(Result, aChildType, aItem);

inc(FCount);

end;

procedure TtdBinarySearchTree.Insert(aItem : pointer);

var

ChildType : TtdChildType;

begin

bstInsertPrim(aItem, ChildType);

end;

Для выполнения большей части работы мы используем внутреннюю процедуру bstInsertPrim. Это делается для того, чтобы разделить код собственно вставки и код метода Insert, что впоследствии упростит нашу задачу при создании производных деревьев от дерева бинарного поиска для выполнения операции балансировки. Как видите, процедура bstInsertPrim возвращает вставленный узел и использует метод bstFindItem, который уже встречался в листинге 8.13.

Таким образом, фактическую вставку мы делегируем объекту бинарного дерева, который использует свой метод InsertAt.