Анализ алгоритмов
Рассмотрим два возможных варианта поиска в массиве элемента "John Smith": последовательный поиск и бинарный поиск. Мы напишем код для обоих вариантов, а затем определим производительность каждого из них. Реализация простого алгоритма последовательного поиска приведена в листинге 1.1.
Листинг 1.1. Последовательный поиск имени в массиве элементов
function SeqSearch( aStrs : PStringArray;
aCount : integer; const aName : string5): integer;
var
i : integer;
begin
for i := 0 to pred(aCount) do
if CompareText(aStrs^[i], aName) = 0 then begin
Result := i;
Exit;
end;
Result := ‑1;
end;
В листинге 1.2 содержится код более сложного бинарного поиска. (пока что мы не будем объяснять, что происходит в этом коде. Алгоритм бинарного поиска подробно рассматривается в главе 4.)
Очень трудно оценить быстродействие каждого из приведенных кодов только по самому их виду. Это основной принцип, которому мы должны всегда следовать: нельзя оценивать скорость работы кода по его виду. Единственным методом определения быстродействия должно быть его выполнение. И только. Если есть возможность выбирать между несколькими алгоритмами, как в рассматриваемом случае, то для выбора более эффективного алгоритма с нашей точки зрения нужно оценить время выполнения кода в различных условиях и на различных исходных данных.
Традиционно для оценки времени работы кода используется профилировщик (profiler). Профилировщик загружает тестируемое приложение и точно измеряет время выполнения отдельных подпрограмм. Профилировщик рекомендуется использовать во всех случаях. Только профилировщик поможет определить, на что тратится большая часть времени выполнения кода, а, следовательно, над какими подпрограммами стоит поработать с целью увеличения быстродействия всего приложения.
Листинг 1.2. Бинарный поиск имени в массиве элементов
function BinarySearch( aStrs : PStringArray;
aCount : integer; const aName : string5): integer;
var
L, R, M : integer;
CompareResult : integer;
begin
L := 0;
R := pred(aCount);
while (L <= R) do begin
M := (L + R) div 2;
CompareResult := CompareText(aStrs^[M], aName);
if (CompareResult = 0) then begin
Result := M;
Exit;
end
else
if (CompareResult < 0) then
L :=M + 1
else
R := M ‑ 1;
end;
Result := ‑1;
end;
В компании TurboPower Software, где работает автор книги, используется профессиональный профилировщик из пакета Sleuth QA Suite. Все коды, приведенные в книге, были протестированы как с помощью StopWatch (название профилировщика из пакета Sleuth QA Suite), так и с помощью Code Watch (название отладчика использования ресурсов и утечки памяти из пакета Sleuth QA Suite). Тем не менее, даже если у вас нет своего профилировщика, вы можете проводить тестирование и определять время выполнения. Просто это не совсем удобно, поскольку в код приходится помещать вызовы функций работы со временем. Нормальные профилировщики не требуют внесения в код изменений, они оценивают время за счет изменения выполняемого файла в памяти компьютера непосредственно в процессе выполнения.
Для тестирования и определения времени выполнения алгоритмов поиска была написана специальная программа. Фактически она определяет системное время вначале перед, а затем и после выполнения кода. По результатам определения времени вычисляется время выполнения. Принимая во внимание, что в настоящее время компьютеры стали достаточно мощными, а часы системного времени характеризуются сравнительно низкой точностью, как правило, для более точной оценки быстродействия код выполняется несколько сот раз, а затем определяется среднее значение. (Кстати, эта программа была написана в среде 32‑разрядной Delphi и не будет компилироваться под Delphi1, поскольку она выделяет память для массивов из кучи, которая превышает граничное для Delphi1 значение 64 Кб.)
Эксперименты по оценке быстродействия алгоритмов проводились различными способами. Сначала для обоих алгоритмов было определено время, необходимое для поиска фамилии "Smith" в массивах из 100, 1000, 10000 и 100000 элементов, которые содержали искомый элемент. В следующей серии экспериментов осуществлялся поиск того же элемента в массивах того же размера, но при отсутствии в них искомого элемента. Результаты экспериментов приведены в таблице 1.1.
Таблица 1.1. Времена выполнения последовательного и бинарного поиска
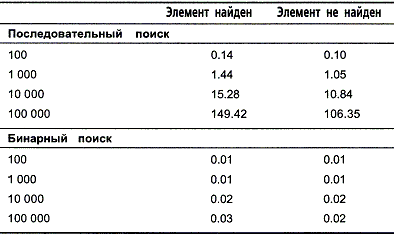
Как видно из таблицы, эксперименты показали очень интересные результаты. Время выполнения последовательного поиска пропорционально количеству элементов в массиве. Таким образом, можно сказать, что характеристики выполнения последовательного поиска линейны.
Результаты выполнения бинарного поиска проанализировать сложнее. Может даже показаться, что из‑за очень быстрого выполнения алгоритма при определении времени мы столкнулись с проблемой потери точности. Очевидно, что зависимость между количеством элементов в массиве и временем выполнения алгоритма не является линейной. Но по приведенным данным трудно определить тип зависимости.
Эксперименты были проведены повторно. При этом времена выполнения умножались на коэффициент 100.
Таблица 1.2. Повторное тестирование бинарного поиска
Эти данные более достоверны. Из них видно, что десятикратное увеличение количества элементов в массиве приводит к увеличению времени выполнения на определенную постоянную величину (примерно на 0.5). Это логарифмическая зависимость, т.е. время бинарного поиска пропорционально логарифму количества элементов в массиве.
(Если вы не математик, то вам будет не так легко это понять. Вспомните из своих школьных дней, что для вычисления произведения двух чисел можно вычислить их логарифмы, сложить их, а затем определить антилогарифм суммы. Поскольку в рассматриваемых экспериментах количество элементов умножается на 10, то в логарифмической зависимости это будет эквивалентно прибавлению константы. Как раз это мы и видим в результатах экспериментов: для каждого последующего массива время увеличивается на 0.5.)
Что мы узнали из результатов проведенных экспериментов? Во‑первых, теперь мы знаем, что единственным методом определения быстродействия алгоритма является оценка времени его выполнения.
‑‑‑‑
В общем случае, единственным методом определения быстродействия отдельной части кода является оценка времени ее выполнения. Это справедливо как в отношении широко известных алгоритмов, так и в отношении алгоритмов, разработанных лично вами. Не нужно предполагать, просто измерьте время выполнения.
‑‑‑‑
Во‑вторых, мы определили, что по своей природе последовательный поиск является линейным, а бинарный поиск ‑ логарифмическим. Если быть поближе к математике, то можно взять эти статистические результаты и теоретически доказать их справедливость. Тем не менее, в этой книге мы не будет перегружать текст математическими выкладками. Можно найти немало книг, в которых приведены эти выкладки (см., например, тома "Фундаментальные алгоритмы на С++" и "Фундаментальные алгоритмы на С" Роберта Седжвика, вышедшие в свет в издательстве "Диасофт").