
- •Часть 3
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Правила оформления
- •Рабочая учебная программа
- •Часть 2 254
- •Часть 3 102
- •Часть 4 152
- •Пояснительная записка
- •1. Контрольные работы
- •2. Учебно-методические материалы по дисциплине
- •3. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Теоретический раздел Глава 1. Дифференциальные уравнения и системы дифференциальных уравнений. Элементы теории устойчивости
- •§1. Основные понятия теории дифференциальных уравнений
- •§2. Дифференциальные уравнения 1-го порядка, интегрируемые в квадратурах
- •II. Дифференциальные уравнения с разделяющимися переменными
- •III. Дифференциальные уравнения с однородными функциями
- •V. Уравнения Бернулли
- •VI. Дифференциальные уравнения, обладающие интегрирующими множителями, зависящими от одной переменной.
- •§3. Дифференциальные уравнения высших порядков
- •§4. Линейные дифференциальные уравнения n-го порядка
- •§5. Линейные неоднородные дифференциальные уравнения (лнду) с произвольными коэффициентами
- •§6. Системы дифференциальных уравнений
- •Метод исключения.
- •Метод интегрируемых комбинаций
- •§7. Введение в теорию устойчивости
- •§8. Устойчивость по Ляпунову
- •§9. Классификация точек покоя однородной системы двух линейных дифференциальных уравнений первого порядка с постоянными действительными коэффициентами
- •§10. Исследование на устойчивость решений нелинейных систем. Устойчивость по первому приближению
- •Глава 2. Кратные, криволинейные и поверхностные интегралы. Теория поля (ж.А.Черняк, а.А. Карпук, в.А. Ранцевич) §1. Двойной интеграл. Определение и свойства
- •§2. Тройной интеграл
- •§3. Вычисление кратных интегралов в прямоугольной декартовой системе координат
- •Переход от прямоугольных декартовых координат к полярным в двойном интеграле
- •§4. Цилиндрические и сферические координаты
- •§5. Криволинейные интегралы 1-го рода
- •§6. Криволинейные интегралы 2-го рода
- •§7. Поверхностный интеграл 1-го рода (пи-1)
- •§8. Поверхностный интеграл второго рода
- •§9. Элементы теории поля и векторного анализа
- •1. Оператор Гамильтона (набла)
- •Глава 3. Числовые и функциональные ряды
- •§1. Числовые ряды. Основные определения и понятия
- •§2. Признаки сходимости положительных рядов
- •§3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§4. Функциональные ряды
- •§5. Равномерная сходимость функционального ряда. Основные свойства равномерно сходящихся рядов
- •§6. Степенные ряды
- •§7. Разложение функции в степенной ряд. Ряд Тейлора
- •§8. Приложения степенных рядов
- •Методические указания к выполнению контрольной работы 7
- •Тесты для самопроверки
- •Контрольная работа 8. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 8
- •Тесты для самопроверки
- •Контрольная работа 9. Ряды. Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 9
- •Тесты для самопроверки
- •Радикальный признак Коши.
- •Интегральный признак Коши.
- •6. Знакочередующие ряды. Признак Лейбница. Знакопеременные ряды.
- •8. Применение степенных рядов.
V. Уравнения Бернулли
Дифференциальные уравнения вида
![]() ,
(2.6)
,
(2.6)
где
![]() ,
называются
уравнениями Бернулли.
,
называются
уравнениями Бернулли.
При
![]() уравнение (2.6) превращается в линейное
дифференциальное уравнение первого
порядка.
уравнение (2.6) превращается в линейное
дифференциальное уравнение первого
порядка.
При
![]() - в дифференциальное уравнение с
разделяющимися переменными.
- в дифференциальное уравнение с
разделяющимися переменными.
Пусть
![]() и
и
![]() .
Очевидно, что
.
Очевидно, что
![]() является решением этого уравнения. Для
является решением этого уравнения. Для
![]() разделим уравнение (2.5) на
разделим уравнение (2.5) на
![]() .
При этом получим:
.
При этом получим:
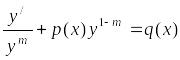 .
.
Введем
новую неизвестную функцию
![]() ,
тогда
,
тогда
 .
.
В итоге получаем:
 – линейное
дифференциальное уравнение первого
порядка, вид интегрирующего множителя
для которого определяется теоремой
2.2.
– линейное
дифференциальное уравнение первого
порядка, вид интегрирующего множителя
для которого определяется теоремой
2.2.
Замечание.
Уравнения Бернулли и их частный случай
– линейные дифференциальные уравнения
первого порядка – можно также
проинтегрировать методом Бернулли,
суть которого в замене неизвестной
функции
произведением двух новых неизвестных
функций
![]() и
и
![]() .
.
VI. Дифференциальные уравнения, обладающие интегрирующими множителями, зависящими от одной переменной.
Рассматривая линейные дифференциальные уравнения первого порядка, можно заметить, что интегрирующий множитель этих уравнений зависит только от переменной . На самом деле существует гораздо более широкий класс уравнений первого порядка, помимо линейных, для которых определяются интегрирующие множители, зависящие либо только от , либо только от . Достаточные условия принадлежности дифференциальных уравнений к этому классу описываются следующей теоремой.
Теорема 2.3.
Пусть для уравнения (2.1)
либо
функция
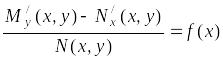 зависит только от переменной
,
зависит только от переменной
,
либо
функция
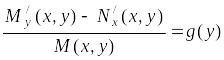 зависит только от переменной
зависит только от переменной
![]() .
.
Тогда в первом случае существует интегрирующий множитель уравнения (2.1) вида
![]() .
.
Во втором случае существует интегрирующий множитель уравнения (2.1) вида
![]() .
.
Пример.
Найти общий интеграл дифференциального уравнения
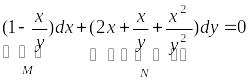 в
области
в
области
![]() .
.
Проверим,
выполняются ли для этого условия теоремы
2.1 в указанной области:
 .
.
![]() .
.
Составим
разность
 .
.
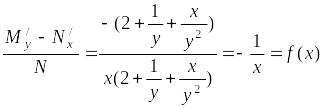 .
.
Таким образом, в соответствии с теоремой 2.3, существует интегрирующий множитель
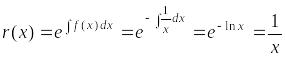 .
.
После
умножения на
![]() уравнение становится точным:
уравнение становится точным:
 .
.
Его
общий интеграл имеет вид
![]() ,
где
,
где
![]() ,
,
 ,
значит
,
значит
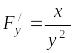 ,
,
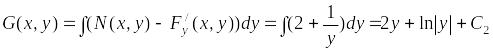
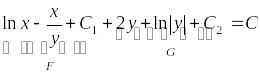 ,
,
 – общий
интеграл дифференциального уравнения.
– общий
интеграл дифференциального уравнения.
§3. Дифференциальные уравнения высших порядков
Если порядок дифференциального уравнения выше первого порядка, то оно называется дифференциальным уравнением высшего порядка.
Если
уравнение
-го
порядка
![]() разрешимо относительно старшей
производной, то его можно записать в
виде:
разрешимо относительно старшей
производной, то его можно записать в
виде:
![]() (3.1)
(3.1)
В рамках данного параграфа будем отождествлять понятия интегральной кривой и решения дифференциального уравнения (3.1).
Будем
говорить, что интегральная кривая
![]() дифференциального
уравнения (3.1) «проходит» через заданную
точку
дифференциального
уравнения (3.1) «проходит» через заданную
точку
![]() пространства
пространства![]() ,
если выполняется система уравнений:
,
если выполняется система уравнений:
 (3.2)
(3.2)
Система (3.2) называется системой начальных условий.
Задача
Коши для дифференциального уравнения
(3.1) ставится следующим образом: найти
интегральную кривую
,
проходящую через точку![]() .
.
Для дифференциального уравнения второго порядка можно определить геометрический и механический смысл задачи Коши:
 (3.3)
(3.3)
Геометрический
смысл задачи (3.3)
заключается в нахождении интегральной
кривой
,
которая проходит на плоскости через
точку
![]() и имеет в этой точке заданный угловой
коэффициент наклона касательной
и имеет в этой точке заданный угловой
коэффициент наклона касательной
![]() .
.
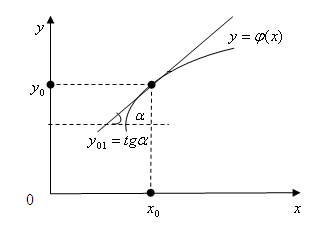
Механический смысл задачи (3.3).
Если
- закон прямолинейного движения точки,
где
- время, то условие
![]() задает начальное положение движущейся
точки, а
задает начальное положение движущейся
точки, а
![]() - начальную скорость точки.
- начальную скорость точки.
Пусть![]() - открытая область пространства
- открытая область пространства
![]() .
Будем говорить, что дифференциальное
уравнение (3.1) в точке
обладает
свойством локальной единственности
решения, если существует хотя бы одна
интегральная кривая дифференциального
уравнения (3.1), проходящая через точку
,
при этом найдется такой интервал
.
Будем говорить, что дифференциальное
уравнение (3.1) в точке
обладает
свойством локальной единственности
решения, если существует хотя бы одна
интегральная кривая дифференциального
уравнения (3.1), проходящая через точку
,
при этом найдется такой интервал![]() ,
для которого все интегральные кривые
уравнения, проходящие через заданную
точку
,
совпадают.
,
для которого все интегральные кривые
уравнения, проходящие через заданную
точку
,
совпадают.
Теорема 3.1 (Коши).
Если
в области
пространства
правая часть дифференциального
уравнения(3.1)
![]() и её частные производные
и её частные производные
![]() непрерывны, то в каждой точке
,
принадлежащей данной области
,
дифференциальное уравнение (3.1) обладает
свойством локальной единственности
решения.
непрерывны, то в каждой точке
,
принадлежащей данной области
,
дифференциальное уравнение (3.1) обладает
свойством локальной единственности
решения.
Дадим определения общего, частного и особого решений интеграла дифференциального уравнения (3.1).
Пусть
в области
пространства
дифференциальное уравнение (3.1) обладает
свойством локальной единственности
решения. Функция![]() ,
где
,
где![]() - независимые константы,
- независимые константы,
![]() ,
называется общим решением дифференциального
уравнения (3.1) в области
,
если:
,
называется общим решением дифференциального
уравнения (3.1) в области
,
если:
для любых допустимых фиксированных значений констант
 функция
функция
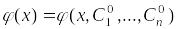 является частным решением дифференциального
уравнения (3.1);
является частным решением дифференциального
уравнения (3.1);для любой точки , принадлежащей области , можно указать такие значения констант
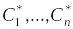 ,
что функция
,
что функция является интегральной кривой
дифференциального уравнения (3.1),
проходящей через точку
является интегральной кривой
дифференциального уравнения (3.1),
проходящей через точку
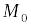 .
.
Если общее (частное) решение получено в неявном виде, оно называется общим (частным) интегралом дифференциального уравнения (3.1).
Решение дифференциального уравнения (3.1) называется особым, если в каждой его точке нарушено свойство локальной единственности решения.

Пример.
Рассмотрим
дифференциальное уравнение второго
порядка
![]() и проверим, является ли функция
и проверим, является ли функция
 общим решением дифференциального
уравнения.
общим решением дифференциального
уравнения.
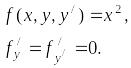
Поскольку
эти функции непрерывны во всем
пространстве
![]() ,
то в силу теоремы 3.1 в области
,
то в силу теоремы 3.1 в области
![]() уравнение обладает свойством локальной
единственности решения.
уравнение обладает свойством локальной
единственности решения.
В области проверим свойства 1) -2) из определения общего решения.
Возьмем произвольные константы
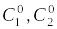

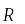 :
:
![]()
 ,
тогда
,
тогда
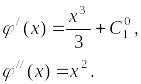
Значит, - решение уравнения.
Пусть задана точка
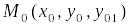
 .
Решим систему уравнений
.
Решим систему уравнений

относительно
констант
![]()
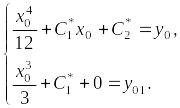
Значит,
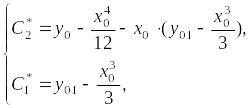
Функция
![]() задает ту интегральную кривую, которая
проходит через заданную точку
.
задает ту интегральную кривую, которая
проходит через заданную точку
.
Дифференциальные уравнения высших порядков, допускающие понижение порядка.
Говорят, что дифференциальное уравнение высшего порядка допускает понижение порядка, если в нем можно сделать такую замену переменной, что полученное в результате уравнение будет иметь порядок меньший, чем порядок исходного уравнения. Даже если полученное в результате понижения порядка уравнение решается численно, это делается эффективнее, чем для первоначального уравнения.
Рассмотрим три основных типа таких уравнений.
I. Дифференциальные уравнения вида
![]() ,
,
где
![]() известная
функция, интегрируются в квадратурах.
известная
функция, интегрируются в квадратурах.
Действительно,
учитывая, что
![]() ,
и интегрируя по
левую и правую части уравнения, получаем
уравнение
,
и интегрируя по
левую и правую части уравнения, получаем
уравнение
![]() порядка
порядка
![]() .
.
Поскольку это уравнение того же типа, что и исходное, находим
![]() .
.
Через шагов получим общее решение уравнения :
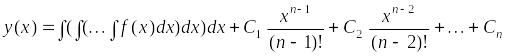 .
.
Пример.
Найти
общее решение уравнения
![]() .
.
Последовательно интегрируя трижды, находим общее решение:
 ,
,
![]() ,
,
 ,
,
для
![]()
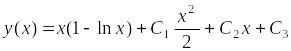 ,
,
для
![]()
 ,
,
 –общее
решение уравнения.
–общее
решение уравнения.
II.
Дифференциальные
уравнения не содержащие неизвестной
функции и
её первых
![]() производных, т.е.
имеющие вид
производных, т.е.
имеющие вид

Пусть
![]() новая
неизвестная функция, тогда
новая
неизвестная функция, тогда
![]() ,
,
![]()
![]()
Таким образом, уравнение примет вид
![]()
следовательно, порядок уравнения понижен на единиц.
Пример.
Найти
общее решение уравнения
![]() .
.
Пусть
![]() ─ новая неизвестная функция, тогда
─ новая неизвестная функция, тогда
![]() и
данное уравнение примет вид
и
данное уравнение примет вид
![]() ,
,
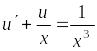 .
.
Это линейное дифференциальное уравнение первого порядка с интегрирующим множителем
![]() .
.
Умножив обе части уравнения на интегрирующий множитель , получим
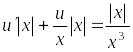
или
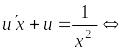
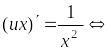
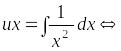
![]() .
.
По
условию
![]() .
Подставив
в последнее уравнение, получим
.
Подставив
в последнее уравнение, получим
![]()
или
 ,
,
откуда находим общее решение
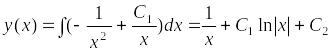 .
.
III. Дифференциальные уравнения не содержащие явно независимой переменной x. Их общий вид
![]() .
.
Порядок
этого уравнения можно понизить
подстановкой
![]() ,
где
,
где
![]() рассматривается как новая неизвестная
функция, а
принимается за независимую переменную.
В этом случае все производные
рассматривается как новая неизвестная
функция, а
принимается за независимую переменную.
В этом случае все производные
![]()
![]()
![]() надо выразить через производные от
функции
надо выразить через производные от
функции
![]() по
:
по
:
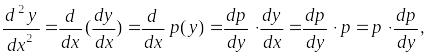
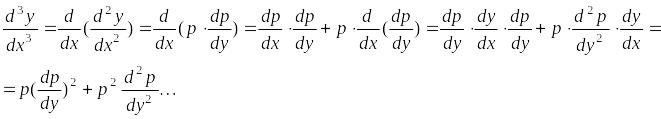 Поскольку
производные
Поскольку
производные
![]() выражаются через функцию
выражаются через функцию
![]() и её производные по
,
порядок которых не превосходит
и её производные по
,
порядок которых не превосходит
![]() ,
то после указанной замены уравнение
понизит свой порядок на единицу.
,
то после указанной замены уравнение
понизит свой порядок на единицу.
Пример.
Найти
общее решение уравнения
![]() .
.
Пусть
![]() новая независимая переменная,
новая независимая переменная,
![]() новая неизвестная функция, тогда
новая неизвестная функция, тогда
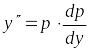 .
Дифференциальное уравнение в результате
примет вид:
.
Дифференциальное уравнение в результате
примет вид:

