II. Дифференциальные уравнения с разделяющимися переменными
Если в дифференциальном уравнении (2.1) коэффициенты имеют вид
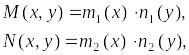
то уравнение
(2.4)
называется дифференциальным уравнением с разделяющимися переменными.
Проверим,
что функция
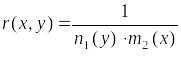является интегрирующим множителем
дифференциального уравнения (2.4).Умножив
уравнение (2.4) на
,
получим уравнение
.
Это уравнение является точным уравнением вида (2.3) с разделёнными переменными. Следовательно, его общий интеграл имеет следующий вид:
.
Пример.
Найти общий интеграл дифференциального уравнения
.
Запишем уравнение в симметричном виде
.
Полученное уравнение является дифференциальным уравнением с разделяющимися переменными. В этом случае его интегрирующий множитель равен
.
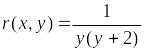Следовательно, точное уравнение имеет следующий вид:
.
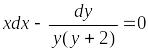А общий интеграл выглядит так:
.
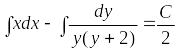Так
как
,
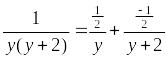то
,
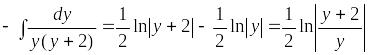а значит, общий интеграл данного уравнения в итоге имеет вид:
.
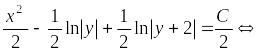
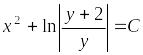III. Дифференциальные уравнения с однородными функциями
Определение.
Функция
называется однородной
функцией
-
го порядка
в открытом прямоугольнике
,
если для любого допустимого значения
параметра
выполняется равенство
в каждой точке
.
Данное равенство является характеристическим свойством однородной функции.
Пример.
Функция
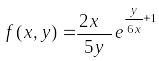является однородной функцией нулевого
порядка, так как для любого
.
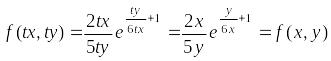Пример.
Пусть
.
Тогда для любого
.
Отсюда
,
следовательно, это однородная функция
2-го порядка.
Определение.
Уравнение
(2.1) называется дифференциальным
уравнением с однородными функциями,
если его коэффициенты
и
являются
однородными функциями одного и того же
порядка.
Пусть в уравнении (2.1) и однородные функции порядка . Очевидно, что уравнение (2.1) в этом случае можно привести к виду
,
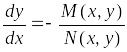где
функция
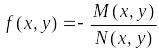является однородной функцией 0-го
порядка, т.е.
.
Тогда,
взяв
,
получим
Сделаем
замену неизвестной функции
в
уравнении
по
формуле
,
где
новая
неизвестная функция.
Тогда
,
.
Подставив
и
в уравнение (с),
получим
Покажем, что полученное уравнение есть дифференциальное уравнение (2.4) с разделяющимися переменными. Действительно, симметричный вид этого уравнения
,
а его интегрирующий множитель равен
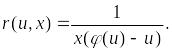
Тогда соответствующее ему точное дифференциальное уравнение и его общий интеграл имеют вид:
,
,
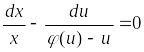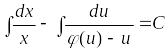где
.
IV. Линейные дифференциальные уравнения 1-го порядка
Дифференциальное уравнение
, (2.5)
где
функции
,
называемые его коэффициентами, непрерывны
на некотором интервале
,
называется линейным
дифференциальным уравнением 1-го порядка.
Название
уравнения (2.5) обусловлено тем, что
и
входят
в него линейно.
Сформулируем теорему о виде интегрирующего множителя линейного дифференциального уравнения 1-го порядка.
Теорема 2.2. Дифференциального уравнения (2.5) обладает интегрирующим множителем
.
Доказательство.
После умножения уравнения (2.5) на
получим
или в симметричном виде:
.
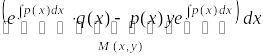
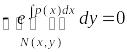В
соответствии с теоремой 2.1 достаточно
проверить, что
в прямоугольнике
.
,
.
Поскольку
,
то
интегрирующий множитель уравнения
(2.5).Теорема доказана.
Пример.
Решим
линейное уравнение
с помощью интегрирующего множителя.
Поскольку
,
то
.
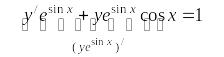
Значит,
– общий интеграл данного уравнения.