§2. Дифференциальные уравнения 1-го порядка, интегрируемые в квадратурах
Дифференциальными уравнениями, интегрируемыми в квадратурах, называются уравнения, общие решения (интегралы) которых выражаются через известные функций с помощью конечного числа алгебраических операций и операций вычисления неопределённых интегралов.
Если
уравнение (1.2)
удаётся записать в виде
,
(2.1)
то
будем говорить, что уравнение записано
в симметричной относительно переменных
x
и y
форме. В
частности, уравнение
всегда можно записать в симметричной
форме, так как
,
т.е.
.
Уравнение
(2.1) называется точным
(в полных дифференциалах), если функции
и
имеют непрерывные частные производные
1-ого порядка в прямоугольнике
и при этом существует функция
,
определенная в
,
для которой левая часть уравнения (2.1)
является ее полным дифференциалом, т.е.
.
Таким
образом, уравнение (2.1) в этом случае
равносильно уравнению
.
Из этого следует, что общий интеграл
уравнения (2.1) имеет вид:
,
где
– произвольная константа.
Теорема 2.1.
Пусть
коэффициенты уравнения (2.1)
И
имеют непрерывные частные производные
первого порядка в прямоугольнике
.
Уравнение (2.1) в этом случае является
точным
тогда и только тогда, когда
в любой точке
,
принадлежащей прямоугольнику
.
Доказательство.
Дано:
уравнение (2.1) – точное. Доказать, что
.
Так
как уравнение (2.1) является точным, то
существует такая функция
,
что
.
С другой стороны,
.
Сравнивая два представления
,
заключаем, что
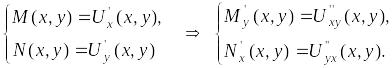
Смешанные
производные равны тогда и только тогда,
когда они непрерывны. Поскольку функции
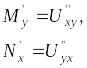– непрерывны, то по теореме о равенстве
смешанных производных
в любой точке
.
Дано:
в любой точке
,
принадлежащей прямоугольнику
.
Доказать, что уравнение (2.1) является
точным.
По
определению уравнение (2.1) является
точным, если существует такая функция
,
что
.
Докажем, что функция вида
,
где
на интервале
,
на интервале
,
является искомой, т.е.
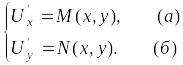
Начнем
с доказательства
. 
.
Чтобы
доказать равенство
,
установим, что функция
не зависит от
.
Рассмотрим подынтегральное выражение
:
для
любой точки
.
Из этого следует, что подынтегральная
функция
не зависит от переменной
,
а, следовательно, и сама функция
тоже не зависит от
.
Таким
образом,
,
т.е. равенство
доказано.
В итоге, функция – искомая, что и требовалось доказать.
Вывод для практики.
Общий интеграл точного уравнения (2.1) имеет вид:
,
(2.2)
где на интервале ;
на интервале ;
– константа.
Пример.
Найти общий интеграл дифференциального уравнения.
.
Обозначим:
,
.
Проверим, является ли это уравнение
точным:
,
для
любой точки
.
Вычислим
и
.
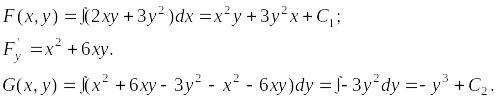
Искомая
функция
будет равна:
общий интеграл исходного уравнения
имеет вид
.
Поскольку свойство дифференциального уравнения (2.1) “быть точным” зависит от вида его коэффициентов, то возможна корректировка этих коэффициентов с тем, чтобы превратить неточное уравнение в точное. Одним из таких “корректировщиков” является интегрирующий множитель.
Определение.
Функция
в прямоугольнике
называется интегрирующим
множителем
уравнения
(2.1), если дифференциальное уравнение
является точным в прямоугольнике
.
Исходя из этого определения и теоремы 2.1 очевидно, что задача интегрирования уравнения (2.1) равносильна задаче нахождения интегрирующего множителя для этого уравнения. В общем случае для произвольного уравнения (2.1) интегрирующий множитель найти невозможно. Опишем некоторые частные случаи уравнения (2.1), для которых можно отыскать интегрирующий множитель.
I. Дифференциальные уравнения с разделенными переменными
Если коэффициенты уравнения (2.1) имеют вид
,
то дифференциальное уравнение
(2.3)
называется дифференциальным уравнением с разделёнными переменными.
Очевидно, что уравнение (2.3) – точное, так как
,
а его общий интеграл в соответствии с формулой (2.2) имеет следующий вид:
.