Контрольная работа 8. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля Указания к выбору варианта

Последняя цифра личного шифра (после дефиса) определяет номер варианта. Если последняя цифра 0, то номер варианта 10.

Задания

Задача 351 - 360.

Вычислить площадь фигуры, ограниченной заданными линиями, с помощью двойного интеграла.

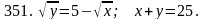
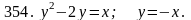
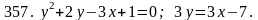
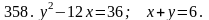
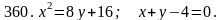
Задача 361 - 370.

Вычислить двойной интеграл, перейдя к полярным координатам.

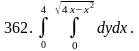
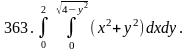
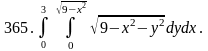
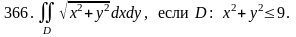
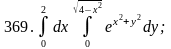
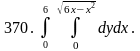
Задача 371 - 380.

Найти объем тела, ограниченного заданными поверхностями, с помощью тройного интеграла.

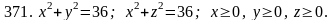
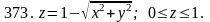
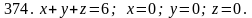
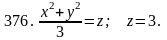
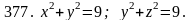
Задача 381 - 390.

Вычислить криволинейный интеграл второго рода вдоль заданной линии .

 дуга кривой 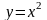от точки 0(0;0) до В(1;1).

дуга кривой 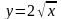от точки 0(0;0) до А(1;2).

 линия 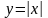от точки А(-1;1) до В(2;2).

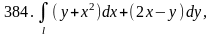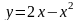 дуга кривой от точки А(1;1) до В(3;-3).

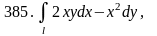 дуга кривой 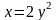от точки А(0;0) до В(2;1).

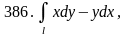дуга кривой от точки 0(0;0) до А(2;8).

 кривая, заданная параметрически

 дуга кривой от точки 0(0;0) до А(2;4).

 дуга кривой 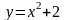от точки А(0;2) до В(1;3).

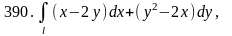 дуга кривой 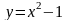от точки 0(1;0) до А(2;3).

Задача 391 - 400.

Найти поток векторного поля 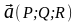через заданную поверхность .

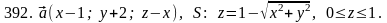
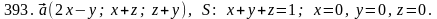
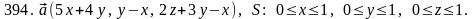
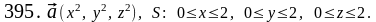
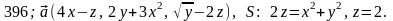
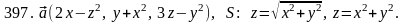
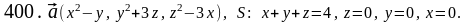
Задача 401 - 410.

Проверить, будет ли потенциальным и соленоидальным поле F. В случае потенциальности поля найти его потенциал U (x,y,z).

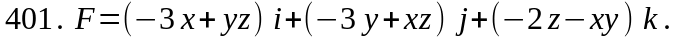
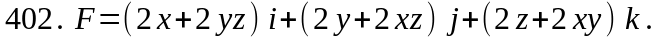
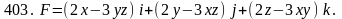
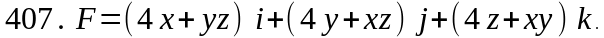
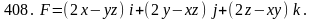
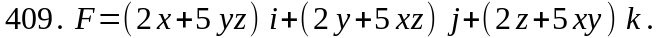
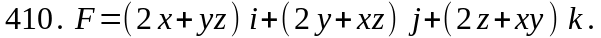
Методические указания к выполнению контрольной работы 8

Пример 1. Вычислить площадь криволинейной трапеции, ограниченной линиями

Решение.

Построим график заданных границ (рис. 1). Для этого преобразуем уравнение к виду

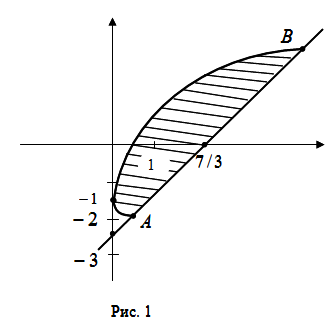
Вершина М в точке (0;-1). Парабола пересекает прямую в точках А и В

координаты которых находятся из системы уравнений

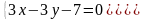
Точка А имеет координаты и В 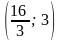. Удобнее внешней переменной интегрирования выбрать Тогда

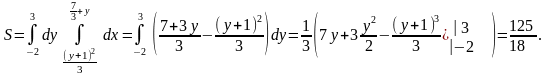
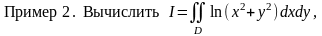
если G – кольцо между окружностями

Решение.

Перейдем к полярным координатам

.

Взяв внутренний интеграл по частям, получим I=e²(3e²–1).

Пример 3.

С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями

.

Решение.

Сделаем чертеж (рис.2). Поверхности 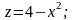; 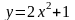– параболические цилиндры.

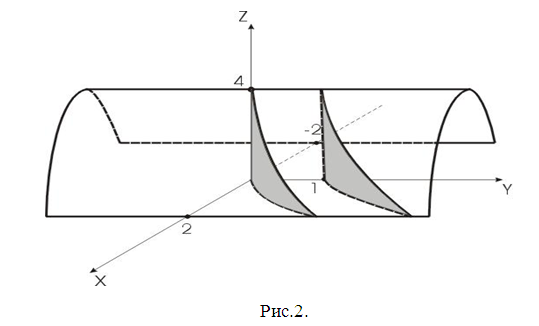
Тело симметрично относительно координатной плоскости YOZ, поэтому вычислим половину рассмотренного объема и результат умножим на 2:

.

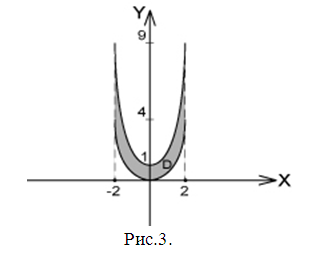
Рис. 3

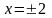Область D в плоскости xOy есть область, ограниченная снизу кривой , а сверху кривой и с боков прямыми ( при 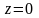имеем 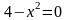) (рис.3).

Для первой четверти х изменяется от 0 до 2, у изменяется от нижней кривой до верхней .

Поэтому, расставив пределы интегрирования, получим

.

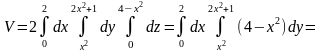
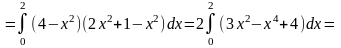
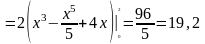Пример 4(А). Вычислить криволинейный интеграл

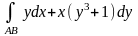
вдоль дуги параболы от точки A(0;0) до точки B(2;2).

Решение.

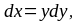
Из уравнения линии интегрирования находим 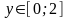. Вычислим криволинейный интеграл, переходя к определенному с переменной интегрирования у:

.

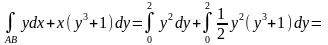
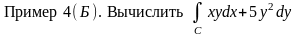
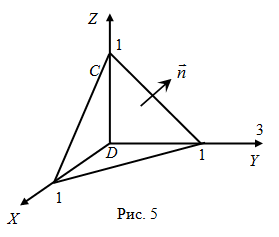
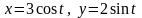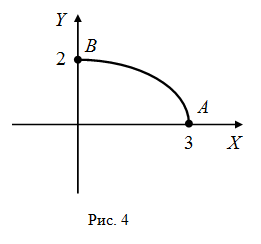
вдоль дуги С эллипса , от точки A(3;0) до точки В(0;2) (рис.4).

Решение.

Дуга С представляет собой часть эллипса в 1-й четверти. В точке А , в точке В .

.

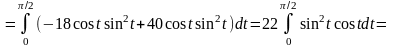
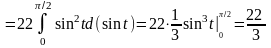Пример 5(А). Вычислить поток векторного поля

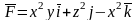
через плоскость треугольника , вырезанного из плоскости 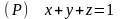координатными плоскостями, в том направлении нормали к плоскости, которая образует с осью 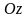острый угол (рис.5).

Решение.

Поток векторного поля вычисляется с помощью поверхностного интеграла по формуле

,

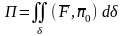где – единичный вектор нормали к поверхности ;

определяется по формуле

,

причем берется знак “ – ” , так как , т.е.

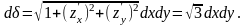
Поэтому вычисление потока по поверхности сводится к вычислению двойного интеграла по проекции на плоскости xOy (D), т.е.

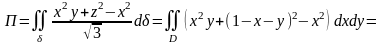
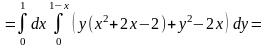
Пример 5(Б). Вычислить поток векторного поля

через внешнюю сторону замкнутой поверхности , образованной поверхностям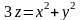и

и

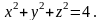
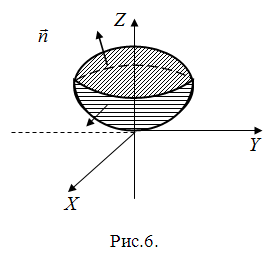
Решение.

Изобразим поверхность , нижняя часть которой является параболоидом, накрытым сферой (верхняя часть) (рис.6).

Так как поверхность замкнута, то применим формулу Остроградского:

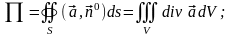
где – тело, ограниченное поверхностью . Поле 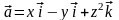определено и дифференцируемо на всем пространстве 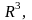и его Поверхности пересекаются по окружности при Тогда поток

В таком виде вычислять интеграл неудобно, поэтому перейдем к цилиндрическим координатам

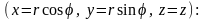
Пример 6. Проверить, будет ли потенциальным и соленоидальным поле . В случае потенциальности поля найти его потенциал U.

Решение.

Найдем по формуле

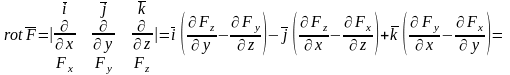
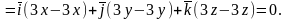
Итак, поле потенциально. Для вычисления потенциала по формуле

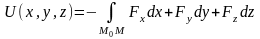
в качестве точки 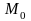возьмем начало координат. Тогда получаем

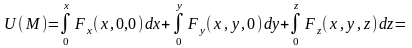
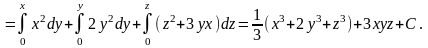
Проверим соленоидальность поля, вычислив

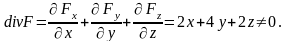
Значит, поле не является соленоидальным.