Тесты для самопроверки

Задание 1. Используя определение решения дифференциального уравнения, проверьте, является ли функция 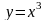решением следующих дифференциальных уравнений:

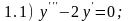
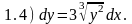
Ответы:

1.1) нет; 1.2) да; 1.3) нет; 1.4) да.

Задание 2. Используя представление производной как отношение дифференциалов , «разделите» переменные в приведенных ниже дифференциальных уравнениях, т.е. приведите уравнения к виду

.

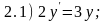
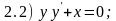
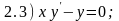
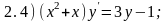
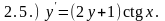
Ответы:

Задание 3. Найдите решения дифференциальных уравнений 2.1 - 2.5, которые в результате выполнения задания 2 были приведены к виду, готовому для интегрирования. В задачах 2.1, 2.3 - 2.5 постоянную интегрирования С запишите в логарифмическом виде.

Ответы:

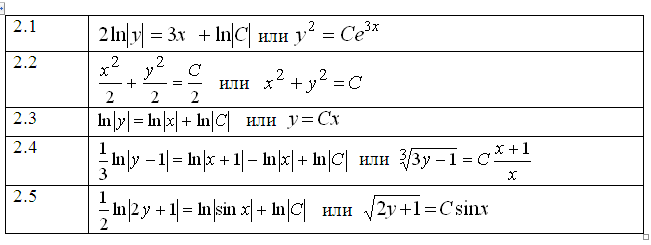
Задание 4. Повторите, как распознаются основные типы дифференциальных уравнений первого порядка:

(А) уравнения с разделяющимися переменными;

(Б) однородные уравнения;

(В) линейные уравнения;

(Г) уравнения Бернулли.

Среди приведенных ниже дифференциальных уравнений укажите номера тех уравнений, которые являются уравнениями типа (А) - (Г).

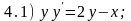
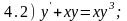
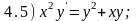
Ответы:

Задание 5. Вспомните методы интегрирования основных типов (А) - (Г) дифференциальных уравнений первого порядка. Проинтегрируйте уравнения 4.1 - 4.6 из задания 4. Для проверки правильности решения этих уравнений определите, решениями каких из уравнений 4.1 - 4.6 являются приведенные ниже функции (а) - (е):

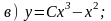
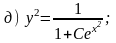
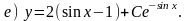
Ответы:

а) 4.6; б) 4.1; в) 4.4; г) 4.5; д) 4.2; е) 4.3.

Задание 6. Приведенные ниже дифференциальные уравнения 2-го порядка разбейте на три группы. К группе А отнесите те дифференциальные уравнения, которые содержат только вторую производную и независимую переменную х; к группе Б - те уравнения, которые не содержат неизвестной функции у; к группе В - уравнения, не содержащие независимой переменной х.

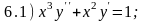
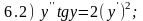
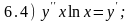
Ответы:

а) 6.3; 6.5; б) 6.2; 6.6; в) 6.1; 6.4.

Задание 7. Вспомните методы понижения порядка для неполных дифференциальных уравнений 2-го порядка. Опираясь на схемы-подсказки, проинтегрируйте уравнения группы А (подсказка 1), группы Б (подсказка 2) и группы В (подсказка 3).

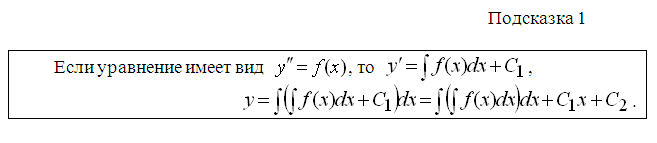
Для проверки правильности полученных результатов определите, решениями каких дифференциальных уравнений 6.1 - 6.6 являются приведенные ниже функции.

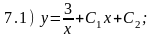
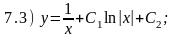
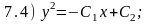
Ответы:

7.1) 6.5; 7.2) 6.3; 7.3) 6.1; 7.4) 6.6; 7.5) 6.4; 7.6) 6.2.

Задание 8. Для каждого из линейных однородных дифференциальных уравнений 8.1 - 8.7 с постоянными коэффициентами составьте характеристическое уравнение, найдите его корни и напишите (в зависимости от характера корней) общее решение уравнения

Подсказка 1

Подсказка 2

;

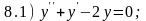
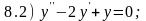
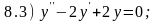
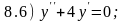
Для проверки правильности выполнения задания каждой функции 8.А - 8.Ж из списка приведенных ответов поставьте в соответствие номер той из задач 8.1 - 8.7, общим решением которой она является.

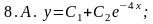
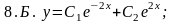
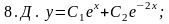
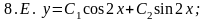
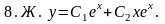
Ответы:

8.А) 8.6; 8.Б) 8.4; 8.И) 8.3; 8.Г) 8.7; 8.Д) 8.1; 8.Е) 8.5.; 8.Ж) 8.2.

Задание 9. Даны линейные неоднородные дифференциальные уравнения 2-го порядка со специальной правой частью. Повторите метод подбора частного решения ỹ для таких уравнений. Напишите частные решения уравнений 9.1 - 9.4, не находя числовых значений их коэффициентов.

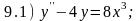
Из списка приведенных ответов 9.А - 9.Р выберите верные, присвоив им номера тех из уравнений 9.1 - 9.4, решениями которых они являются.

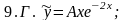
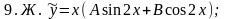
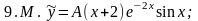
Ответы:

9.1) 9.В; 9.2) 9.Е; 9.3) 9.Л; 9.4) 9.Р.

Задание 10. Даны 2 матрицы

; .

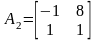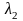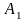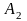а) Найдите собственные значения и матриц и и укажите их среди данных пар чисел 10.1 - 10.5:

10.1 {1; 1}; 10.2. {1; 10}; 10.3. {1; 3};

10.4. {-3; 3}; 10.5. {-3; -3}.

Ответы:

А₁) 10.2; А₂) 10.4.

б) Найдите собственные векторы матриц и и укажите их среди следующих пар векторов 10.6 - 10.9.

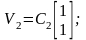
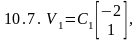
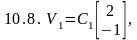
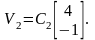
Ответы:

А₁) 10.6; А₂) 10.9.

Задание 11. Решите системы линейных однородных дифференциальных уравнений 11.1, 11.2 с постоянными коэффициентами, используя алгоритм, приведенный в схеме-подсказке.

Подсказка

Среди приведенных ответов 11.А - 11.Г выберите верные.

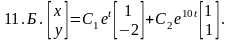
Ответы:

11.1) 11,Б; 11.2) 11.Г.