§8. Приложения степенных рядов

Степенные ряды используются для:

1) представления неэлементарных функций (например, неберущихся интегралов);

2) приближённого вычисления чисел, значений функций и определённых интегралов;

3) приближённого решения алгебраических, дифференциальных и интегральных уравнений.

Пример 1.

Представить в виде суммы ряда неэлементарную функцию

.

Рассмотрим функцию 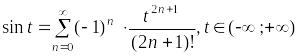, тогда

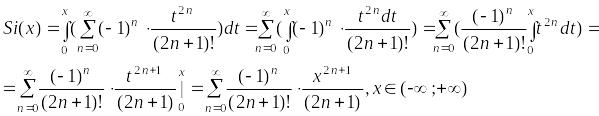
Таким образом,

.

Пример 2.

Вычислить приближённо число с точностью 10^-3.

Используем ряд Маклорена для :

^,

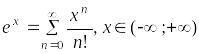откуда при получаем

.

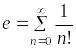Для приближённого вычисления числа найдём такой номер , что

, где .

Тогда

.

Оценим остаток (оценка остатка ряда с факториалами):

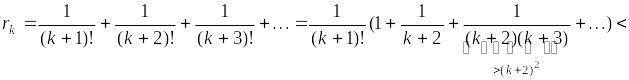
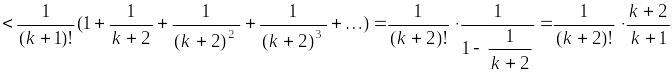
Искомый номер находим, решая неравенство:

.

При ,

при .

Таким образом, число .

Пример 3.

Рассмотрим ЛНДУ го порядка с переменными коэффициентами

^.

Поставим задачу Коши

Справедливо следующее утверждение.

Если коэффициенты данного уравнения разлагаются в ряд Тейлора в окрестности точки , то решение поставленной задачи Коши может быть найдено в виде степенного ряда 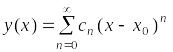, который сходится в указанной окрестности .

Решить задачу Коши:

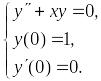
Поскольку все условия утверждения для коэффициентов данного уравнения выполнены, то решение задачи Коши будем искать в виде ряда Маклорена.

.

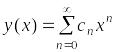Так как , то .

Так как , то .

Тогда

,

,

.

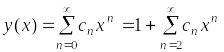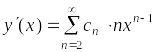Подставим выражения для и в исходное уравнение.

Определим коэффициенты полученного уравнения. Коэффициенты при определяем из равенства:

;

при :

;

при :

.

_{Аналогично}

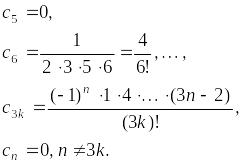
Таким образом, искомое решение задачи Коши является суммой следующего степенного ряда:

.

ПРАКТИЧЕСКИЙ РАЗДЕЛ

Контрольные работы

Контрольная работа 7. Дифференциальные уравнения

Указания к выбору варианта

Последняя цифра личного шифра (после дефиса) определяет номер варианта. Если последняя цифра 0, то номер варианта 10.

Задания

Задача 301 – 310.

301-310. Найти решение дифференциального уравнения 1-го порядка.

Задача 311 – 320.

Найти общее решение дифференциального уравнения 1-го порядка.

Задача 321 - 330.

Найти частное решение дифференциального уравнения 1-го порядка.

Задача 331 - 340.

Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.

Задача 341 - 350.

Найти общее решение системы уравнений (рекомендуем решать с помощью характеристического уравнения).

Методические указания к выполнению контрольной работы 7

Пример 1. Решить уравнение

Решение. Это уравнение с разделяющимися переменными. Разделив почленно на , получим

Потенцируя последнее равенство, получим и, освобождаясь от модуля, получим или , где С – произвольная постоянная, отличная от нуля (как положительная, так и отрицательная). Разделив на , мы могли потерять решения, обращающие в нуль произведение . Полагая , находим, что . Непосредственная подстановка их в уравнение показывает, что они действительно являются решениями. Но эти решения могут быть получены из общего решения

Таким образом, все решения содержатся в общем интеграле

Пример 2. Решить уравнение

Решение. Запишем уравнение в виде

удовлетворяет условию

то исходное уравнение однородное. Замена переменной

приводит его к уравнению с разделяющимися переменными

. Последнее выражение представляет собой общий интеграл уравнения. В ходе решения мы могли потерять решения вида

(так как делили на это выражение обе части уравнения). Непосредственной подстановкой убеждаемся, что не является решением уравнения. Множитель дает решения , которые не могут быть получены из общего интеграла ни при каких С. Поэтому  особые решения, а общий интеграл дается формулой .

Пример 3. Решить уравнение

Решение. Это линейное неоднородное уравнение первого порядка. Будем искать его решение в виде

Подставив и в исходное уравнение, получим

Для нахождения неизвестных функций и потребуем, чтобы выражение обращалось в ноль:

Тогда функцию найдем из уравнения

Теперь запишем решение

которое и является общим интегралом исходного уравнения.

Пример 4. Найти общее решение дифференциального уравнения.

Решение.

то это уравнение в полных дифференциалах.

Найдем и приравняем к

или – общий интеграл дифференциального уравнения.

Пример 5. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям .

Решение.

Рассмотрим соответствующее однородное линейное уравнение . Его характеристическое уравнение имеет вид . Корни уравнения различны и действительны. Значит, общее решение соответствующего однородного уравнения имеет вид . Правая часть исходного уравнения , т.е. является также корнем характеристического уравнения, поэтому частное решение ищем в виде

Для нахождения коэффициентов продифференцируем дважды и подставим в первоначальное уравнение:

После сокращения на и приведения подобных членов получим

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях тождественного равенства, получим

и общее решение данного уравнения имеет вид:

.

Чтобы найти решение, удовлетворяющее начальным условиям , , продифференцируем общее решение

и решим относительно и систему уравнений

Исходное частное решение имеет вид

Пример 6. Решить систему

Решение.

Применим метод исключения. Для этого дифференцируем первое уравнение по

Из первого уравнения выражаем

и, подставив в предыдущее уравнение, получим

Это однородное линейное уравнение с постоянными коэффициентами. Для его решения составим характеристическое уравнение , корни которого

Тогда общее решение однородного уравнения имеет вид

Таким образом, общее решение имеет вид

Пример 7. Решить систему

Решение.

Применим метод Эйлера. Запишем систему в матричной форме:

Будем искать частное решение в виде , , где – константы. Составляем характеристическое уравнение матрицы системы:

Находим и из системы уравнений

При получаем из системы . Помножив , получим . Таким образом, характеристическому числу соответствует частное решение Аналогично для находим Общее решение системы находим как линейную комбинацию полученных частных решений, т.е.

или в матричной форме