
- •Часть 3
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Правила оформления
- •Рабочая учебная программа
- •Часть 2 254
- •Часть 3 102
- •Часть 4 152
- •Пояснительная записка
- •1. Контрольные работы
- •2. Учебно-методические материалы по дисциплине
- •3. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Теоретический раздел Глава 1. Дифференциальные уравнения и системы дифференциальных уравнений. Элементы теории устойчивости
- •§1. Основные понятия теории дифференциальных уравнений
- •§2. Дифференциальные уравнения 1-го порядка, интегрируемые в квадратурах
- •II. Дифференциальные уравнения с разделяющимися переменными
- •III. Дифференциальные уравнения с однородными функциями
- •V. Уравнения Бернулли
- •VI. Дифференциальные уравнения, обладающие интегрирующими множителями, зависящими от одной переменной.
- •§3. Дифференциальные уравнения высших порядков
- •§4. Линейные дифференциальные уравнения n-го порядка
- •§5. Линейные неоднородные дифференциальные уравнения (лнду) с произвольными коэффициентами
- •§6. Системы дифференциальных уравнений
- •Метод исключения.
- •Метод интегрируемых комбинаций
- •§7. Введение в теорию устойчивости
- •§8. Устойчивость по Ляпунову
- •§9. Классификация точек покоя однородной системы двух линейных дифференциальных уравнений первого порядка с постоянными действительными коэффициентами
- •§10. Исследование на устойчивость решений нелинейных систем. Устойчивость по первому приближению
- •Глава 2. Кратные, криволинейные и поверхностные интегралы. Теория поля (ж.А.Черняк, а.А. Карпук, в.А. Ранцевич) §1. Двойной интеграл. Определение и свойства
- •§2. Тройной интеграл
- •§3. Вычисление кратных интегралов в прямоугольной декартовой системе координат
- •Переход от прямоугольных декартовых координат к полярным в двойном интеграле
- •§4. Цилиндрические и сферические координаты
- •§5. Криволинейные интегралы 1-го рода
- •§6. Криволинейные интегралы 2-го рода
- •§7. Поверхностный интеграл 1-го рода (пи-1)
- •§8. Поверхностный интеграл второго рода
- •§9. Элементы теории поля и векторного анализа
- •1. Оператор Гамильтона (набла)
- •Глава 3. Числовые и функциональные ряды
- •§1. Числовые ряды. Основные определения и понятия
- •§2. Признаки сходимости положительных рядов
- •§3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§4. Функциональные ряды
- •§5. Равномерная сходимость функционального ряда. Основные свойства равномерно сходящихся рядов
- •§6. Степенные ряды
- •§7. Разложение функции в степенной ряд. Ряд Тейлора
- •§8. Приложения степенных рядов
- •Методические указания к выполнению контрольной работы 7
- •Тесты для самопроверки
- •Контрольная работа 8. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 8
- •Тесты для самопроверки
- •Контрольная работа 9. Ряды. Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 9
- •Тесты для самопроверки
- •Радикальный признак Коши.
- •Интегральный признак Коши.
- •6. Знакочередующие ряды. Признак Лейбница. Знакопеременные ряды.
- •8. Применение степенных рядов.
§7. Разложение функции в степенной ряд. Ряд Тейлора
Пусть
на интервале
функция
является суммой некоторого степенного
ряда
.
Тогда говорят, что на интервале
функция
разлагается в степенной ряд с центром
в точке
![]() (по степеням
(по степеням
![]() ).
).
Вопрос о разложении функции в степенной ряд является одним из важных прикладных вопросов теории степенных рядов. Ставится задача: описать, при каких условиях функция разлагается в степенной ряд в окрестности точки и как определяются коэффициенты этого степенного ряда. Частично на этот вопрос отвечает теорема 7.1.
Теорема 7.1 (необходимые условия разложимости функции в степенной ряд).
Если
функция
разлагается в степенной ряд
в
некоторой окрестности
точки
,
то его коэффициенты
![]() находятся по формулам
находятся по формулам
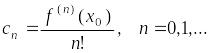 ,
,
а
значит,
![]()
![]() должна быть бесконечно дифференцируема
в точке
.
должна быть бесконечно дифференцируема
в точке
.
Доказательство.
Пусть функция
в окрестности
![]() является суммой степенного ряда, то
есть
является суммой степенного ряда, то
есть
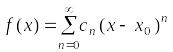 .
Тогда
.
Тогда
![]() ,
где
–
-я
частичная сумма ряда, а
–
-й
частичный остаток ряда.
,
где
–
-я
частичная сумма ряда, а
–
-й
частичный остаток ряда.
При
этом
![]()
![]() при
при
![]() .
.
Таким
образом,
![]() при
.
при
.
Но
из курса математического анализа
известно, что никакой другой многочлен,
кроме многочлена Тейлора, не может
приблизить данную функцию
в окрестности
с точностью
![]() при
при
![]() .
Следовательно,
.
Следовательно,
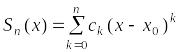 – многочлен Тейлора, а значит, его
коэффициенты являются коэффициентами
Тейлора, то есть
,
что и требовалось доказать.
– многочлен Тейлора, а значит, его
коэффициенты являются коэффициентами
Тейлора, то есть
,
что и требовалось доказать.
В связи с теоремой 7.1. дается определение ряда Тейлора для функции в точке .
Определение.
Степенной ряд
с коэффициентами
,
называется рядом Тейлора для функции
в точке
,
независимо от того, сходится ли он вообще
или сходится ли он к данной функции
.
Если
![]() ,
ряд
,
ряд
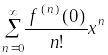 называется рядом Маклорена для функции
.
называется рядом Маклорена для функции
.
Можно привести примеры, когда ряд Тейлора, составленный для функции с центром в точке , расходится всюду, кроме точки , или сходится, но совсем к другой функции.
Пример Коши (функции, для которой ряд Маклорена сходится к другой функции).
Рассмотрим
функцию
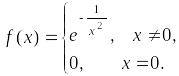

Вычислим коэффициенты Маклорена для функции :
![]()
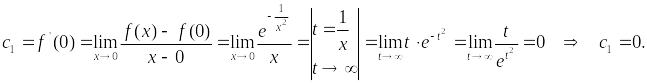 Аналогично,
Аналогично,
![]()
Ряд Маклорена для функции имеет вид:
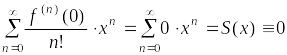 ,
т.е.
,
т.е.
![]() .
.
Таким образом возникает вопрос, какие условия должны выполняться, чтобы Функция разлагалась в ряд Тейлора.
Теорема 7.2 (достаточные условия разложения функции в ряд Тейлора).
Пусть
функция
в некоторой окрестности
точки
имеет производные любого порядка
,
которые равномерно ограничены в этой
окрестности, т.е. существует такое число
,
при котором
![]() для любого натурального
в любой точке
.
Тогда в этой окрестности функция
разлагается в ряд Тейлора:
для любого натурального
в любой точке
.
Тогда в этой окрестности функция
разлагается в ряд Тейлора:
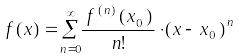 .
.
Доказательство. Так как в окрестности функция имеет производные любого порядка, то для нее в этой окрестности можно записать формулу Тейлора любого порядка :
![]() ,
,
где
![]() – многочлен Тейлора,
– многочлен Тейлора,
![]() – остаточный член формулы Тейлора
порядка
.
– остаточный член формулы Тейлора
порядка
.
Запишем в форме Лагранжа:
 ,
где
,
где
![]() .
Заметим, что поскольку
.
Заметим, что поскольку
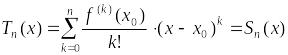 ,
то
,
то
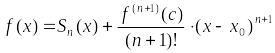 ,
где
,
где
![]() –
-я
частичная сумма ряда Тейлора. Исходя
из последней формулы, достаточно
показать, что
–
-я
частичная сумма ряда Тейлора. Исходя
из последней формулы, достаточно
показать, что
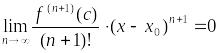 для любого
,
тогда для любого
для любого
,
тогда для любого
![]() ,
то есть
,
по определению, является суммой ряда
Тейлора на интервале
.
,
то есть
,
по определению, является суммой ряда
Тейлора на интервале
.
Оценим остаточный член :
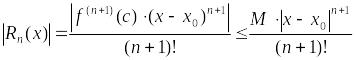 и
покажем, что
и
покажем, что
 для любого
.
для любого
.
Составим
функциональный ряд
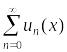 ,
где
,
где
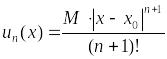 .
Найдем радиус сходимости
данного ряда.
.
Найдем радиус сходимости
данного ряда.
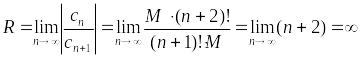 .
Следовательно,
сходится на всей числовой прямой, а
значит,
.
Следовательно,
сходится на всей числовой прямой, а
значит,
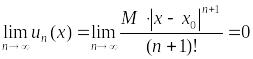 ,
что и требовалось доказать.
,
что и требовалось доказать.
Теорема 7.3 (разложение в ряд Маклорена некоторых элементарных функций).
Справедливы следующие разложения в ряды Маклорена:
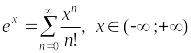 – разложение
экспоненты в ряд Маклорена.
– разложение
экспоненты в ряд Маклорена.
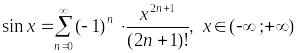 – разложение
синуса в ряд Маклорена.
– разложение
синуса в ряд Маклорена.
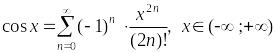 – разложение
косинуса в ряд Маклорена.
– разложение
косинуса в ряд Маклорена.
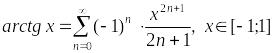 – разложение
арктангенса в ряд Маклорена.
– разложение
арктангенса в ряд Маклорена.
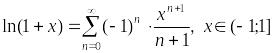 – разложение
логарифма в ряд Маклорена.
– разложение
логарифма в ряд Маклорена.
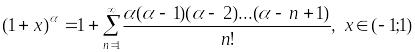 – биномиальное
разложение.
– биномиальное
разложение.
Доказательство. Очевидно, что ряды, записанные в этих равенствах справа, являются рядами Маклорена для соответствующих функций (см. соответствующие формулы Маклорена). Остается доказать, что ряды Маклорена сходятся к указанным слева в этих равенств функциям.
Для
функций
![]() ,
,
![]() ,
,
![]() используем результаты теоремы 7.2. На
каждом фиксированном промежутке
используем результаты теоремы 7.2. На
каждом фиксированном промежутке
![]() ,
где
,
где
![]() ,
все производные этих функций равномерно
ограничены. Действительно,
,
все производные этих функций равномерно
ограничены. Действительно,
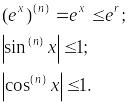
Следовательно, по теореме 7.2 данные функции являются суммами своих рядов Маклорена.
Докажем справедливость 4-го разложения.
Рассмотрим
степенной ряд
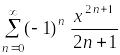 .
.
Найдём
его радиус сходимости
![]() :
:
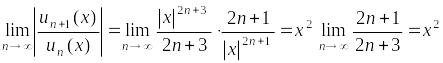 .
.
Ряд
сходится абсолютно, если
![]() и расходится при
и расходится при
![]() .
Отсюда следует, что радиус сходимости
.
Отсюда следует, что радиус сходимости
![]() .
.
Изучим сходимость на концах интервала.
Пусть , тогда числовой ряд
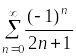 сходится
условно как ряд Лейбница.
сходится
условно как ряд Лейбница.
Пусть
![]() ,
тогда ряд
,
тогда ряд
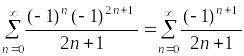 ведёт
себя аналогично.
ведёт
себя аналогично.
В
итоге:
![]() –
область сходимости исходного ряда.
–
область сходимости исходного ряда.
Пусть
на отрезке
![]()
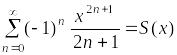 .
Найдём
почленным дифференцированием:
.
Найдём
почленным дифференцированием:
 .
.
Отсюда
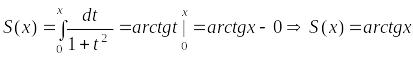 ,
,
что и требовалось доказать.
Аналогично доказывается справедливость 5-й формулы.
6-я формула приводится без доказательства.
Теорема доказана.
