§6. Степенные ряды

Степенным рядом называется функциональный ряд вида

, (6.1)

при этом числа называются коэффициентами ряда, а точка – центром разложения ряда (6.1).

Поскольку -й член степенного ряда является простейшим многочленом, -ая частичная сумма

является многочленом степени , то задача приближенного вычисления суммы ряда сводится к задаче приближения функции многочленом степени .

Для простоты изложения в степенном ряде (6.1) сделаем замену переменной. Пусть , тогда ряд принимает вид

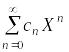(6.2)

и является рядом по степеням . Центром разложения ряда (6.2) является точка . Очевидно, что область сходимости степенного ряда – не пустое множество. Так, для ряда (6.1) точка , а для ряда (6.2) точка . В отличие от произвольных функциональных рядов область сходимости степенных рядов имеет очень простую структуру.

Теорема 6.1 (первая теорема Абеля).

Пусть степенной ряд (6.2) сходится в точке , тогда он сходится абсолютно для любого , удовлетворяющего неравенству (т.е. в интервале ) и на любом отрезке ряд (6.2) сходится равномерно.

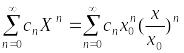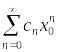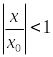Доказательство. Рассмотрим ряд . Так как ряд по условию сходится, то (необходимое условие сходимости), а, следовательно, последовательность – ограничена. Это означает существование такого числа , что для любого . Возьмем любое . Так как , то . Тогда 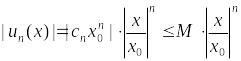. Пусть 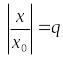, следовательно, а значит, ряд сходится абсолютно.

Если же задан отрезок , то для любого . По признаку Вейерштрасса ряд равномерно сходится на отрезке . Теорема доказана.

Следствие 6.2.

Если степенной ряд (6.2) расходится в точке , то он расходится также и в любой точке , удовлетворяющей неравенству , т.е. расходится на множестве .

Доказательство. Если предложить противное, т.е. в точке , ряд сходится, то по теореме Абеля он сходится и в точке , т.к. . Противоречие.

Следствие 6.3 (о структуре области сходимости степенного ряда (6.2)).

Степенной ряд либо сходится на всей числовой прямой, либо существует такое число , что в интервале ряд сходится, а вне интервала – расходится.

Число в этом случае называется радиусом сходимости степенного ряда (6.2), а интервал называется интервалом сходимости этого ряда. В случае, когда , интервал сходимости вырождается в точку – центр разложения ряда. Если ряд сходится на интервале , то его радиус сходимости .

В соответствие со следствием 6.3 степенные ряды (6.1) и (6.2) сходятся в следующих интервалах.

Вопрос о нахождении радиуса сходимости степенного ряда решается в теореме 6.4.

Теорема 6.4.

Пусть дан степенной ряд 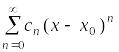, все коэффициенты которого отличны от нуля ( ).

1. Тогда если существует предел 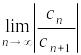, то он совпадает с радиусом сходимости степенного ряда.

2. Если же существует предел 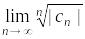, то радиус сходимости

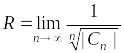(формула Коши – Адамара).

Приведем доказательство первой формулы.

Доказательство. Пусть существует предел . Найдем область сходимости степенного ряда 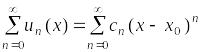. Воспользуемся признаком Даламбера:

(*)

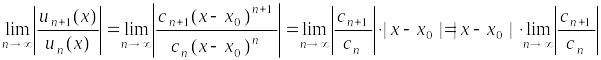Пусть , тогда при в силу (*)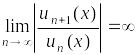 , следовательно, ряд расходится всюду, кроме точки , то есть радиус сходимости ряда .

Пусть , тогда в силу выражения (*):

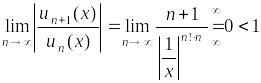следовательно, ряд сходится для всех , а значит, .

Пусть , тогда 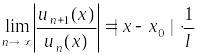и при ряд сходится, а при ряд расходится.

Можно сделать вывод, что если

Тогда по определению радиуса сходимости: , что и требовалось доказать.

Пример.

Дан степенной ряд 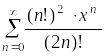. Найти радиус сходимости, интервал и область сходимости ряда.

.

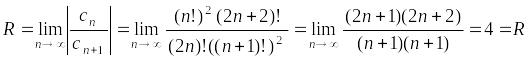Отсюда следует, что .

Исследуем поведение ряда в точках .

При имеем знакоположительный ряд ,

Составим отношение

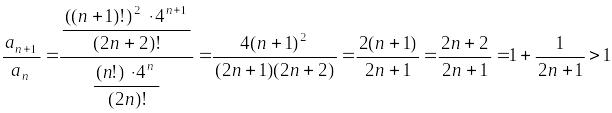Поскольку, 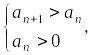то (не выполнено необходимое условие сходимости), значит, ряд расходится.

При .

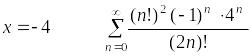Поскольку 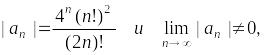то и , а значит, в точке ряд расходится.

Таким образом, областью сходимости ряда является интервал .

Определение. Степенной ряд называется рядом «с пропусками», если он имеет бесконечное множество нулевых коэффициентов.

Например, простейшим рядом «с пропусками» является ряд вида

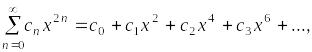где коэффициенты при нечетных степенях равны нулю

Для таких рядов радиус сходимости не может быть найден по теореме 6.4, поэтому его нахождение основывается на общих методах определения области абсолютной сходимости функциональных рядов.

Пример.

Найти радиус сходимости ряда «с пропусками».

.

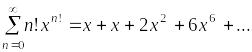
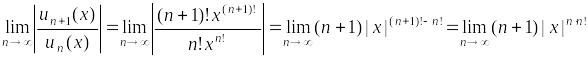Если выполняется неравенство , то

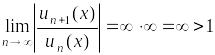, следовательно, ряд расходится.

Если выполняется неравенство , то

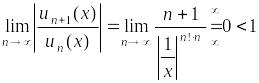, значит, ряд сходится.

Таким образом, областью сходимости ряда «с пропусками» является

Теорема 6.5 (свойства суммы степенного ряда).

Пусть степенной ряд сходится в интервале , где . Тогда сумма ряда

1. непрерывна на интервале ,

2. интегрируема на любом отрезке , целиком лежащем в ,

3. дифференцируема любое число раз на интервале . При этом ряды, полученные в результате почленного дифференцирования, сохраняют первоначальный радиус сходимости .

Доказательство. Поскольку является непрерывной функцией, интегрируемой и любое число раз дифференцируемой функцией в интервале для любого натурального номера , то осталось показать лишь равномерную сходимость исследуемого степенного ряда.

В силу первой теоремы Абеля (теорема 6.1) исследуемый ряд равномерно сходится на любом отрезке , т.е. условия теорем 5.2, 5.3, 5.4 для данного ряда выполнены. Осталось показать, что ряд, полученный почленным дифференцированием, имеет радиус сходимости .

.

Обозначим . Найдем радиус сходимости этого ряда:

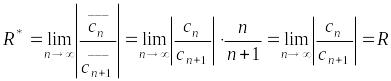, что и требовалось доказать.

Теорема 6.6 (вторая теорема Абеля).

Пусть – сумма степенного ряда 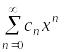в интервале сходимости , где . Тогда если ряд сходится хотя бы в одном из концов интервала, то функция будет непрерывна слева в точке (если ряд сходится в этой точке) и непрерывна справа в точке (если ряд сходится в точке , т.е. либо , либо .

Без доказательства.