
- •Часть 3
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Правила оформления
- •Рабочая учебная программа
- •Часть 2 254
- •Часть 3 102
- •Часть 4 152
- •Пояснительная записка
- •1. Контрольные работы
- •2. Учебно-методические материалы по дисциплине
- •3. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Теоретический раздел Глава 1. Дифференциальные уравнения и системы дифференциальных уравнений. Элементы теории устойчивости
- •§1. Основные понятия теории дифференциальных уравнений
- •§2. Дифференциальные уравнения 1-го порядка, интегрируемые в квадратурах
- •II. Дифференциальные уравнения с разделяющимися переменными
- •III. Дифференциальные уравнения с однородными функциями
- •V. Уравнения Бернулли
- •VI. Дифференциальные уравнения, обладающие интегрирующими множителями, зависящими от одной переменной.
- •§3. Дифференциальные уравнения высших порядков
- •§4. Линейные дифференциальные уравнения n-го порядка
- •§5. Линейные неоднородные дифференциальные уравнения (лнду) с произвольными коэффициентами
- •§6. Системы дифференциальных уравнений
- •Метод исключения.
- •Метод интегрируемых комбинаций
- •§7. Введение в теорию устойчивости
- •§8. Устойчивость по Ляпунову
- •§9. Классификация точек покоя однородной системы двух линейных дифференциальных уравнений первого порядка с постоянными действительными коэффициентами
- •§10. Исследование на устойчивость решений нелинейных систем. Устойчивость по первому приближению
- •Глава 2. Кратные, криволинейные и поверхностные интегралы. Теория поля (ж.А.Черняк, а.А. Карпук, в.А. Ранцевич) §1. Двойной интеграл. Определение и свойства
- •§2. Тройной интеграл
- •§3. Вычисление кратных интегралов в прямоугольной декартовой системе координат
- •Переход от прямоугольных декартовых координат к полярным в двойном интеграле
- •§4. Цилиндрические и сферические координаты
- •§5. Криволинейные интегралы 1-го рода
- •§6. Криволинейные интегралы 2-го рода
- •§7. Поверхностный интеграл 1-го рода (пи-1)
- •§8. Поверхностный интеграл второго рода
- •§9. Элементы теории поля и векторного анализа
- •1. Оператор Гамильтона (набла)
- •Глава 3. Числовые и функциональные ряды
- •§1. Числовые ряды. Основные определения и понятия
- •§2. Признаки сходимости положительных рядов
- •§3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§4. Функциональные ряды
- •§5. Равномерная сходимость функционального ряда. Основные свойства равномерно сходящихся рядов
- •§6. Степенные ряды
- •§7. Разложение функции в степенной ряд. Ряд Тейлора
- •§8. Приложения степенных рядов
- •Методические указания к выполнению контрольной работы 7
- •Тесты для самопроверки
- •Контрольная работа 8. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 8
- •Тесты для самопроверки
- •Контрольная работа 9. Ряды. Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 9
- •Тесты для самопроверки
- •Радикальный признак Коши.
- •Интегральный признак Коши.
- •6. Знакочередующие ряды. Признак Лейбница. Знакопеременные ряды.
- •8. Применение степенных рядов.
§3. Знакопеременные ряды. Абсолютная и условная сходимость
Определение. Числовой ряд называется знакопеременным, если в нем присутствует бесконечно много как положительных, так и отрицательных членов.
К
знакопеременным рядам относятся,
например, следующие ряды
,
где 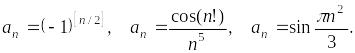
Среди знакопеременных рядов выделяются знакочередующиеся ряды.
Определение. Знакочередующимися рядами называются такие ряды, два соседних члена которых имеют разные знаки.
Примеры.
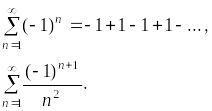
Знакочередующиеся
ряды принято записывать следующим
образом:
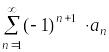 ,
где предполагается, что
.
,
где предполагается, что
.
Для исследования сходимости знакочередующихся рядов используется признак Лейбница.
Теорема 3.1 (признак Лейбница).
Пусть
знакочередующийся ряд
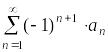 удовлетворяет двум следующим условиям:
удовлетворяет двум следующим условиям:
члены ряда монотонно убывают,
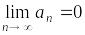 (необходимое
условие сходимости).
(необходимое
условие сходимости).
Тогда исходный ряд сходится.
Доказательство.
Рассмотрим частичную сумму ряда
![]() .
Покажем, что последовательность частичных
сумм
.
Покажем, что последовательность частичных
сумм
![]() монотонно возрастает и ограничена
сверху, а следовательно, сходится.
монотонно возрастает и ограничена
сверху, а следовательно, сходится.
![]() .
.
Это означает, что последовательность ограничена сверху.
С
другой стороны,
![]() ,
то есть последовательность
монотонно возрастает. Обозначим
,
то есть последовательность
монотонно возрастает. Обозначим
![]()
Поскольку,
![]() то
то
![]()
Следовательно,
существует предел последовательности
частичных сумм
,
равный
![]() ,
то есть ряд
сходится. Теорема доказана.
,
то есть ряд
сходится. Теорема доказана.
Ряды, удовлетворяющие условиям признака Лейбница, называются рядами Лейбница.
Следствие 3.2.
Для
ряда Лейбница
выполняются следующие неравенства:
![]() ;
;
![]()
Доказательство.
Из доказательства признака Лейбница
известно, что
![]() ,
следовательно,
,
следовательно,
![]() .
Поскольку
-й
остаток
ряда Лейбница сам является рядом
Лейбница, то для него верна аналогичная
оценка:
.
Поскольку
-й
остаток
ряда Лейбница сам является рядом
Лейбница, то для него верна аналогичная
оценка:
Следствие доказано.

Пояснение:
Рассмотрим
ряд, у которого
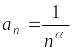 .
.
1)
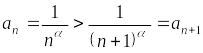 , то есть члены ряда монотонно убывают;
, то есть члены ряда монотонно убывают;
2)
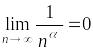 .
Таким образом, условия признака Лейбница
выполняются.
.
Таким образом, условия признака Лейбница
выполняются.

Пояснение:
Если
![]() то при
то при
![]() последовательность
последовательность
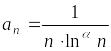 монотонно убывая стремится к нулю, т.е.
имеем ряд Лейбница.
монотонно убывая стремится к нулю, т.е.
имеем ряд Лейбница.
Если
![]() ,
тогда
-й
член ряда примет вид:
,
тогда
-й
член ряда примет вид:
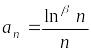 .
.
Рассмотрим
функцию
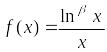 ,
где
.
,
где
.
Найдем производную этой функции:
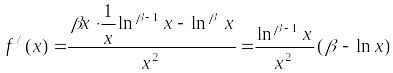 .
.
![]() ,
если
,
если
![]()
![]()
![]() .
.
То
есть для
![]() монотонно стремится к нулю при
.
Значит, ряд
монотонно стремится к нулю при
.
Значит, ряд
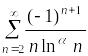 сходится при любом
,
так как удовлетворяет условиям теоремы
3.1.
сходится при любом
,
так как удовлетворяет условиям теоремы
3.1.
Рассмотрим произвольный знакопеременный ряд
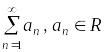 . (3.1)
. (3.1)
Ряд (3.1) определяет два знакопостоянных ряда:
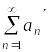 и
и
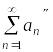 ,
(3.2)
,
(3.2)
где – это й по порядку неотрицательный член ряда (3.1);
– это й по порядку отрицательный член ряда (3.1).
Относительно рядов (3.2) возможны 4 следующие ситуации:
(А)
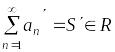 – ряд из неотрицательных членов
сходится;
– ряд из неотрицательных членов
сходится;
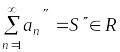 – ряд
из отрицательных членов тоже сходится.
– ряд
из отрицательных членов тоже сходится.
(В) 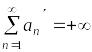 – ряд из неотрицательных членов
расходится;
– ряд из неотрицательных членов
расходится;
– ряд из отрицательных членов сходится.
(С) – ряд из неотрицательных членов сходится;
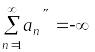 – ряд из отрицательных членов
расходится.
– ряд из отрицательных членов
расходится.
(D) – ряд из неотрицательных членов расходится;
– ряд из отрицательных членов тоже расходится.
Очевидно, что в ситуации (А) ряд (3.1) сходится, а в ситуациях (В) и (С) расходится. В ситуации (D) исходный ряд (3.1) может как сходиться, так и расходиться.
Применительно к рассмотренным случаям дадим два определения.
Знакопеременный
ряд
называется абсолютно
сходящимся,
если ряд, составленный из модулей его
членов
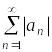 ,
сходится. Знакопеременный ряд
называется условно
сходящимся,
если сам ряд
сходится, а ряд, составленный из модулей
его членов
,
расходится.
,
сходится. Знакопеременный ряд
называется условно
сходящимся,
если сам ряд
сходится, а ряд, составленный из модулей
его членов
,
расходится.
Легко видеть, что абсолютно сходящийся ряд может возникнуть только в ситуации (А). Условие абсолютной сходимости оказывается в этом случае более сильным, чем условие обычной сходимости. А именно, справедливо следующее утверждение.
Утверждение 3.3.
Если ряд (3.1) абсолютно сходится, то он сходится и в обычном смысле.
Доказательство.
Пусть ряд
сходится, тогда ряд
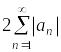 тоже сходится. Используя очевидное
неравенство
тоже сходится. Используя очевидное
неравенство
![]() ,
,
можно
утверждать, что в силу признака сравнения
(теорема 2.1) ряд
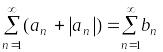 сходится, но с другой стороны
сходится, но с другой стороны
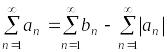 .
.
Поскольку
ряды
![]() и
сходятся, то ряд
,
как их разность, тоже сходится, что и
требовалось доказать.
и
сходятся, то ряд
,
как их разность, тоже сходится, что и
требовалось доказать.
Поскольку
ряд
![]() является знакоположительным рядом, то
для исследования его сходимости можно
использовать все признаки сходимости
и сравнения знакоположительных рядов.
является знакоположительным рядом, то
для исследования его сходимости можно
использовать все признаки сходимости
и сравнения знакоположительных рядов.
Пример.
Исследовать абсолютную сходимость рядов
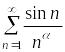 и
и
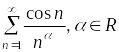 .
.
Поскольку
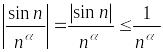 ,
то для
,
то для
![]() ряд
сходится абсолютно, а, следовательно,
и в обычном смысле. Аналогично, ряд
ряд
сходится абсолютно, а, следовательно,
и в обычном смысле. Аналогично, ряд
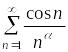 сходится абсолютно для
.
сходится абсолютно для
.
Абсолютно сходящиеся ряды обладают всеми свойствами конечных сумм. Приведём без доказательства некоторые их свойства
Теорема 3.4 (свойства абсолютно сходящихся рядов).
1.
Пусть ряды
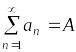 и
и
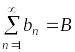 сходятся абсолютно, тогда для любых
чисел
сходятся абсолютно, тогда для любых
чисел
![]() ряд
ряд
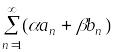 тоже сходится абсолютно к числу
тоже сходится абсолютно к числу
![]() .
.
2. Для любого абсолютно сходящегося ряда допустима произвольная перестановка и произвольная группировка членов ряда. При этом новый ряд будет по-прежнему абсолютно сходящимся к той же сумме.
3.
Пусть даны два числовых ряда
и
.
Произведением этих рядов по Коши
называется ряд
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если хотя бы один из перемножаемых рядов и сходится абсолютно, а другой сходится, то произведение рядов по Коши будет сходиться абсолютно.
Обратимся теперь к условно сходящимся рядам. Очевидно, что такие ряды могут возникнуть только в ситуации (D). Сформулируем несколько свойств условно сходящихся рядов, которые в корне отличаются от свойств абсолютно сходящихся рядов, а, следовательно, и от свойств конечных сумм.
Теорема 3.5.
Если ряд (3.1) условно сходится, то оба ряда (3.2) и расходятся.
Теорема 3.6 (Римана).
Если ряд (3.1) – условно сходящийся, то можно указать такую перестановку его членов, что либо полученный в результате перестановки ряд будет сходиться к любому наперёд заданному числу, либо будет вообще расходиться.
Пример.
Для
всех
![]() исследовать сходимость рядов
исследовать сходимость рядов
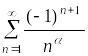 .
.
Известно,
что для
эти ряды абсолютно сходятся, а для
![]() являются рядами Лейбница, т.е сходятся;
для
являются рядами Лейбница, т.е сходятся;
для
![]() ряды расходятся, так как для них не
выполняется необходимое условие
сходимости.
ряды расходятся, так как для них не
выполняется необходимое условие
сходимости.
Аналогично,
ряды
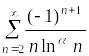 сходятся абсолютно для
,
а для
сходятся абсолютно для
,
а для
![]() сходятся условно.
сходятся условно.
Замечание. Для исследования условной сходимости нельзя применять признаки сравнения знакоположительных рядов.
Приведем пример, когда неправомерное применение признака сравнения приводит к неверному результату.
Пример.
Исследовать
сходимость ряда
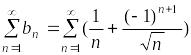 .
.
Ряд
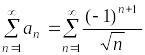 условно сходится (по признаку Лейбница).
условно сходится (по признаку Лейбница).
Исследуемый ряд расходится как сумма сходящегося и расходящегося ряда.
Таким
образом, с точки зрения сходимости, ряды
и
![]() ведут себя по-разному. Однако,
ведут себя по-разному. Однако,
![]() при
,
поскольку
при
,
поскольку
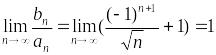 .
.
