1. Оператор Гамильтона (набла)

Определение 11. Символ 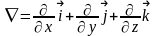называется символическим вектором или оператором Гамильтона (набла-оператором).

С помощью этого оператора можно наглядно представить основные операции векторного анализа.

Например - градиент можно рассматривать как “произведение” символического вектора на скалярную функцию U, т.е.

Дивергенция , как скалярное произведение символического вектора на вектор

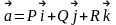
Ротор, как векторное произведение символического вектора на вектор :

Операции 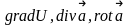называются операциями первого порядка.

Первая и третья порождают векторное поле, вторая – скалярное.

Возможны следующие операции:

, которые называются операциями второго порядка. При этом справедливы сочетания:

Определение 12. Операция второго порядка 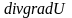называется оператором Лапласа и обозначается , т.е.

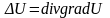
Если поле является одновременно потенциальным и соленоидальным, то 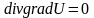и потенциальная функция U является гармонической, т.е. удовлетворяет уравнению Лапласа ( ),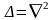

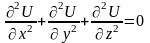
Глава 3. Числовые и функциональные ряды

(Ж.А.Черняк)

§1. Числовые ряды. Основные определения и понятия

Пусть дана числовая последовательность

Составим для этой последовательности выражение следующего вида:

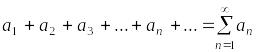, (1.1)

которое назовем числовым рядом.

Если рассмотреть последовательность функций и составить для нее аналогичное выражение 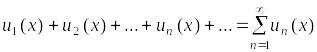, то такое выражение называется функциональным рядом.

Ряды используются для представления, исследования и приближенного вычисления чисел и функций.

Приведем примеры рядов, известные из элементарной математики.

Бесконечная периодическая дробь – это ряд вида .

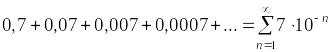Для произвольных, отличных от нуля чисел и выражение 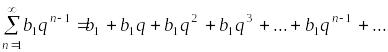– это ряд, составленный из членов бесконечной геометрической прогрессии.

В теории рядов рассматриваются следующие основные вопросы: какие свойства конечных сумм чисел и функций (коммутативность, ассоциативность, почленный переход к пределу, почленное дифференцирование, почленное интегрирование и т.д.) и при каких условиях переносятся на случай «бесконечных» сумм, т.е. рядов?

Теорию рядов начнем с изучения числовых рядов.

Вместе с последовательностью будем рассматривать числовую последовательность , которая строится следующим образом:

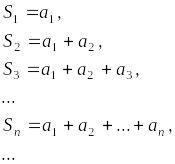
Последовательность называется последовательностью частичных сумм ряда (1.1).

Как и всякая другая числовая последовательность, последовательность может:

1. иметь конечный предел при ;

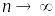2. быть бесконечно большой (то есть );

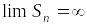3. не иметь никакого предела – ни конечного, ни бесконечного.

Если предел последовательности существует и конечен, то он называется суммой ряда (1.1). При этом пишут .

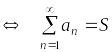В оставшихся двух ситуациях, когда или вообще не существует, ряд (1.1) называется расходящимся.

Понятие суммы для расходящегося ряда не определяется.

Примеры.

1) Рассмотрим числовой ряд

.

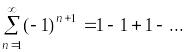Составим для него последовательность частичных сумм:

- колеблющаяся последовательность, откуда следует, что расходится, а значит, исходный числовой ряд является расходящимся.

2) Рассмотрим числовой ряд

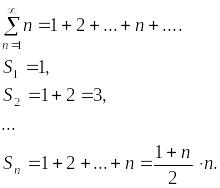
. Значит, – бесконечно большая последовательность, то есть ряд расходится.

3) Пусть - геометрическая прогрессия, , .

Если , то частичная сумма , значит, , то есть ряд расходится.

Если , то 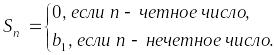, то есть расходится, а значит, и ряд расходится.

Пусть , тогда

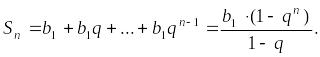
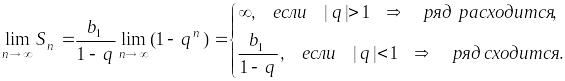
Отметим, что ряд относится к «эталонным» рядам, т.е. используется для исследования сходимости других рядов.

Ряд сходится, если ,

расходится, если

Зададимся вопросом, можно ли, не составляя последовательности частичных сумм , исследовать сходимость числового ряда (1.1)?

Это можно сделать, используя различные признаки сходимости и сравнения рядов. Перейдем к изучению этих признаков.

Теорема 1.1. (необходимое условие сходимости).

Если ряд сходится, то с необходимостью его й член стремится к нулю при . Коротко: сходится .

Доказательство. Пусть ряд сходится, т.е. . Тогда и .

Но ,

что и требовалось доказать.

Сформулируем теорему 1.1 в удобной (для исследования сходимости рядов) форме.

Теорема 1.1.

Если для числового ряда (1.1) или такого предела вообще не существует, то ряд (1.1) расходится.

В такой формулировке теорема 1.1 дает достаточное условие расходимости рядов.

Пример.

Рассмотрим числовой ряд 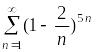и вычислим предел его го члена:

,

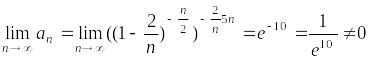следовательно, по теореме 1.1^/ исходный ряд расходится.

Замечание. Важно различать две следующие ситуации:

а) если , то ряд расходится (теорема 1.1^/);

б) если , то сделать вывод о сходимости (расходимости) ряда нельзя.

Пример расходящегося ряда, у которого .

Числовой ряд 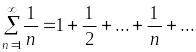называется гармоническим рядом.

(необходимое условие сходимости выполнено).

Покажем, что гармонический ряд расходится. Предположим противное: ряд сходится и 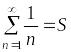. Составим две частичные суммы этого ряда и :

,

.

Так как , то и , а значит, .

С другой стороны, . Но тогда (теорема о переходе к пределу в неравенствах). Полученное противоречие доказывает, что гармонический ряд расходится.

Эталонный ряд: – расходится

Простейшие свойства числовых рядов.

Суммой (разностью) рядов и называется ряд вида .

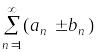Ряд 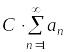по определению совпадает с рядом .

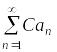1. При умножении ряда 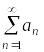на константу, не равную нулю, сходимость (расходимость) не нарушается.

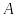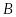2. Если ряды и сходятся к суммам и соответственно, то сумма и разность этих рядов тоже сходится к суммам 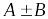соответственно.

Следствие: Если ряд сходится, а ряд расходится, то ряды 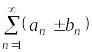расходятся.

3. Если в ряде отбросить конечное число членов (добавить конечное число членов), то ни сходимость, ни расходимость ряда при этом не нарушится.

4. Если ряд сходится к сумме , то члены этого ряда можно произвольно сгруппировать, не меняя порядка следования. При этом полученный в результате ряд сходится к той же сумме.

Свойства I–IV доказываются непосредственно исходя из определения сходимости соответствующих рядов.

Замечание. Если ряды и расходятся, то их сумма (разность) может как сходиться, так и расходиться.

Пример.

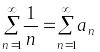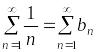Пусть и . Ряды и расходятся.

Сумма этих рядов 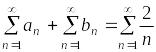расходится в силу свойства I.

Разность этих рядов 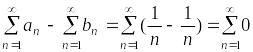сходится.