§6. Криволинейные интегралы 2-го рода

Ориентированные кривые. Задача о работе силового поля вдоль кривой. Определение криволинейного интеграла 2-го рода. Свойства криволинейного интеграла 2-го рода. Вычисление криволинейного интеграла 2-го рода. Связь между криволинейными интегралами 1-го и 2-го рода. Задачи и упражнения.

Пусть в пространстве задана параметрически гладкая кривая равенствами

(6.1)

Точка A = называется начальной точкой кривой , а точка В = - конечной точкой этой кривой.

При изменении параметра от до движение точки по кривой происходит от начальной ее точки А до конечной точки В. При этом единичный вектор касательной ⁰ = /, где вектор  = указывает направление движения (рис. 6.1.).

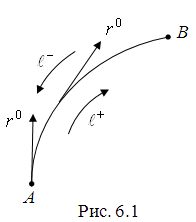
Следовательно, выбор вектора ⁰ однозначно определяет направление движения точки вдоль кривой . Кривая с выбранным на ней направлением движения, определяемым единичным вектором ⁰, называется ориентированной с помощью ⁰. При этом означает, что движение по происходит в направлении вектора ⁰ от начальной точки А к конечной точке В, а - что движение происходит в направлении вектора -⁰, т. е. от В к А ( рис. 6.1).

Для введения понятия криволинейного интеграла 2-го рода решим конкретную задачу – задачу о работе силового поля.

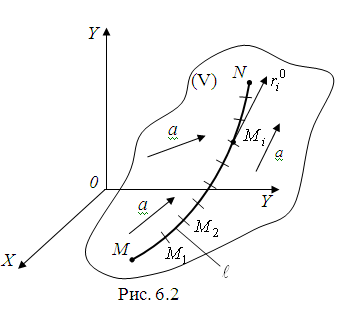
Пусть в каждой точке области V определено непрерывное силовое (векторное) поле a= i + j + k, (рис. 6.2), где , , - непрерывные в области V функции. При перемещении материальной точки силовое поле a совершает некоторую работу А. Для ее определения разобьем произвольную кривую на части длиной . В каждой части выберем произвольно точку Пусть – единичный вектор касательной к кривой в точке (рис. 6.2). Тогда элементарная работа А_i поля a на участке выразится приближенно равенством А_i  (a( ), ) , а вся работа этого поля по кривой приближенно равна сумме (a( ), ) . Обозначим .

Если существует

(a( ), ) ,

не зависящий от способа разбиения на части и от способа выбора точки , то этот предел называется криволинейным интегралом 2-го рода от вектор-функции a по кривой и обозначается

Итак, по определению,

(6.2)

Следовательно, работа А силового поля a по перемещению материальной точки вдоль кривой выражается криволинейным интегралом 2-го рода

А = (6.3)

Получим теперь координатную форму записи криволинейного интеграла 2-го рода (6.2).

При параметрическом задании кривой в виде (6.1) ее дифференциал длины дуги

(6.4)

где τ - вектор касательной к кривой в точке Единичные же вектор касательной в этой точке ⁰ = /. Тогда

Следовательно, криволинейный интеграл в координатной форме запишется в виде:

(6.5)

Приведем теперь без доказательства почти очевидные свойства криволинейных интегралов 2-го рода.

1⁰. (Линейность). Если то

2⁰. (Аддитивность). Если кусочно-гладкая кривая составлена из конечного числа гладких дуг т. е. и части не имеют общих внутренних точек (рис. 6.3), то

_где – единичный вектор касательной в точках части

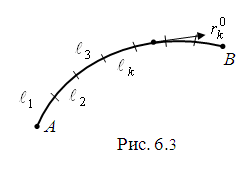
3⁰. Подчеркнем следующее важное свойство криволинейного интеграла (6.5): при изменении ориентации кривой на противоположную криволинейный интеграл 2-го рода меняет знак на противоположный, т. е.

(6.6)

Действительно, если кривая ориентирована единичным вектором касательной ⁰, то при изменении ориентации эта же кривая будет ориентирована вектором -⁰.

Это свойство криволинейного интеграла 2-го рода вполне соответствует физической интерпретации такого интеграла, как работы силового поля вдоль некоторого пути: при изменении направления движения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный.

Криволинейный интеграл 2-го рода часто рассматривается по замкнутой кривой (контуру) . В этом случае его обозначают символом

.

_{При этом обход кривой} называется положительным, если при обходе область , ограниченная контуром , остается с левой стороны. На рис. 6.4

Получим теперь формулы для вычисления криволинейного интеграла 2-го рода при различных способах задания кривой.

Пусть кривая задана параметрически равенствами (6.1). В точках этой кривой вектор-функция a= имеет вид

a=

Отсюда и из (6.5) получаем формулу вычисления криволинейного интеграла 2-го рода в случае параметрического задания пространственной кривой:

(6.7)

Если - плоская кривая, заданная параметрически уравнениями

в точках которой определена непрерывная вектор-функция

a= то формула (6.7) приобретает вид

(6.8)

Пусть теперь плоская кривая задана явно равенством , где - гладкая функция. Ее очевидным образом можно задать параметрически: , Тогда

и, значит, формула (6.8) принимает вид

(6.9)

Пусть - направляющие косинусы вектора ⁰, т. е.

⁰ = Тогда

(6.10)

Так как - это проекция вектора a = на направление касательной к , то, обозначив эту проекцию , мы можем записать криволинейный интеграл 2-го рода в виде

(6.11)

Приведем теперь примеры вычисления криволинейных интегралов 2-го рода.

Пример 6.1. Вычислить интеграл

где AB – дуга параболы заключенная между точками А=(0,0) и В=(2,4).

∆ В данном случае Тогда по формуле (6.9) получаем ▲

Пример 6.2. Вычислить криволинейный интеграл

если - линия пересечения цилиндра с плоскостью (эллипс). Обход эллипса положителен (рис. 6.5).

∆ Составим параметрические уравнения эллипса (он лежит в плоскости , проходящей через начало координат). Проекцией эллипса на плоскость XY является окружность , параметрические уравнения которой Тогда из уравнения плоскости эллипса находим

Таким образом, параметрические уравнения эллипса :

Отсюда по формуле (6.8) имеем:

▲

Пример 6.3. Вычислить работу А силы вдоль отрезка [BC], где B C

∆ Составим параметрические уравнения отрезка [BC]: Тогда работа А силы F на пути [BC] выразится интегралом