§5. Криволинейные интегралы 1-го рода
Рассмотрение различных физических задач, связанных с интегрированием функций вдоль линий, приводит к необходимости введения двух типов криволинейных интегралов, называемых обычно криволинейными интегралами 1-го и 2-го рода. Ниже мы увидим, что эти два типа криволинейных интегралов легко преобразуются друг в друга.
Напомним, что кривая, заданная уравнениями x= x(t), y= y(t), называется гладкой, если функции x(t) и y(t) непрерывны и имеют непрерывные первые производные, не обращающиеся в нуль одновременно (иными словами, если кривая в каждой точке имеет касательную и направление этой касательной непрерывно зависит от точки касания (рис. 5.1а)
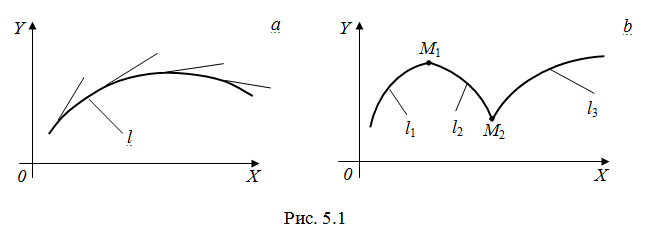
Непрерывная
кривая, составленная из конечного числа
гладких кусков, называется кусочно-гладкой
(на рис. 5.1
b
l=
в
её точках М1
и М2
производные не существуют)
Пусть
l
= AB
– плоская кривая, гладкая или
кусочно-гладкая, в точках которой
определена функция f(x,y).
Кривую
l
точками А
= А
,
А
,
…, А
,
А
,…,
А
=
В
произвольным образом разобьем на части
l
длиной
(рис.
5.2). В части l
выберем
произвольно точку
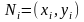и составим интегральную сумму
(5.2)
Обозначим
.
Сумма (5.1) называется интегральной
суммой для функции f(x,y)
по длине дуги кривой.
Если
при
существует конечный предел интегральной
суммы (5.1), не зависящий ни от способа
разбиения кривой l
на части, ни от выбора точек
,
і
=
1, n,
то этот предел называется криволинейным
интегралом 1-го рода
от функции f(x,y)
по кривой l
(интегралом
по длине дуги кривой)
и обозначается
(точка
М = (x,
y)
лежит на кривой l).
Таким образом, по определению
.
В этом случае говорят, что функция f(x,y) интегрируема вдоль кривой l= АВ, кривая АВ называется контуром интегрирования, А - начальной, В - конечной точками интегрирования.
Выясним теперь свойства криволинейных интегралов 1-го рода. Они вполне аналогичны свойствам определенных интегралов. Перечислим основные из них.
1º (Линейность). Если f(x,y) и g(x,y) непрерывные функции вдоль кривой l. Тогда для любых α и β из R
g(x,y)
dl
=
.
2º
(Аддитивность).
Если кусочно-гладкая кривая l
составлена
из конечного числа гладких дуг
,
,
т. е.,
и части
не имеют
внутренних общих точек, то
.
3º (Монотонность). Если f(x,y)- неотрицательная интегрируемая на l функция, то
.
4º
(Оценка
модуля интеграла).
Если f(x,y)
- интегрируема на l
функция, то
также интегрируема на l
и справедливо неравенство
.
5º. 
,
где L
– длина дуги
l.
6º
(Теорема
о среднем).
Если функция f(x,y)
непрерывна на кривой l
(в точках
кривой l),
то существует точка такая
(ξ,η)
,
что
,
где L – длина кривой l.
7º Криволинейный интеграл 1-го рода не зависит от направления пути интегрирования. Это означает, что для l = АВ
.
Укажем теперь некоторые типичные задачи, в которых удобно пользоваться криволинейными интегралами 1-го рода.
Пример 5.1 (масса материальной кривой).
Материальной кривой называется гладкая или кусочно-гладкая кривая, вдоль которой распределена непрерывно некоторая масса с линейной плотностью μ = μ (x,y). Определим массу такой кривой.
Разобьем
дугу l
на части
длина
каждой из которой равна ∆
,
.
Предполагая
плотность участка l
постоянной и равной
μ(xi,yi),
где
,
получаем, что масса части
равна
.
Суммарная
масса всех участков равна
.
Если существует
предел
(
),
то он и
определяет массу дуги l.
Отсюда, согласно определению (5.2), получаем
что искомая масса материальной кривой
.
(5.3)
Пример 5.2 (вычисление координат центра тяжести материальной кривой).
Пусть
масса распределена вдоль кривой l
= АВ
с плотностью μ(x,y).
Разбив эту кривую на n
частей длиной Δ
и выбрав на каждой из них произвольную
точку
,
можно
материальную кривую рассматривать
приближенно как систему масс
,
расположенных
в точках
.
Центр масс С
такой системы материальных точек имеет
координаты (известно из статики)
;
.
(5.4)
Эти выражения можно приближенно считать приближенными значениями координат центра тяжести xc и yc материальной кривой. Для получения точных значений этих координат в равенствах (5.4) перейдем к пределу при
∆ = max Δli → 0. Если они существуют, то в силу (5.2) получим
;
, (5.5)
где m – масса кривой l .
Если кривая однородна (μ = const), то отсюда имеем
;
, (5.6)
где L – длина кривой.
Пример 5.3 (вычисление моментов инерции материальной кривой). Известно, что момент инерции системы точечных масс относительно некоторой прямой равен
,
где ri – расстояние от i -й массы до этой прямой. В частности моменты инерции такой системы масс относительно осей X и Y равны соответственно
,
где
(
)
– координаты точечной массы m
. Для получения моментов инерции
материальной кривой l
, вдоль которой распределена масса с
непрерывной плотностью μ(х,
y), относительно
координатных осей X
и Y,
нужно сделать в (5.6) такой же предельный
переход, как и в предыдущем примере.
Тогда для моментов инерции кривой
относительно осей X
и Y
получим
;
.
(5.7)
Момент инерции I0 кривой относительно начала координат определяется как
.
Пример 5.4 (притяжение точечной массы материальной кривой).
Пусть
снова l
– материальная
кривая с плотностью μ
(х,
y), и m0
- точечная масса, имеющая координаты
(
).
Рассуждения, аналогичные приведенным
выше, показывают, что кривая в соответствии
с законом Ньютона притягивает массу
с силой F,
проекции которой на координатные оси
равны
;
,
(5,8)
где
γ – постоянная тяготения и r
=
.
Как вычисляются криволинейные интегралы 1-го рода?
Пусть
кривая задана явно уравнением y
= g(х),
,
а f
(x,y)
непрерывная в точках этой кривой функция.
Тогда точки (x,y)
кривой имеют вид (х,
g(х)),
,
а функция f
(x,y)
в этих точках имеет вид f
(x,y)
= f
(x,
g(х)).
Так как длина і-й
части
приближенно равна
,
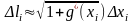то интегральная сумма (5.1) преобразуется
к виду
xi.
Отсюда
в пределе при
получим формулу
для вычисления криволинейного интеграла
в случае явного задания кривой
в виде
y = g(х ), :
.
(5.9)
Если
же кривая
задана параметрически
x
= x
(t),
y
= y(t),
,
то, как мы знаем, в этом случае дифференциал
длины дуги
.
Так как в точках кривой l
функция f(x,y)
= f(x(t),
y
(t)),
,
то
аналогично предыдущему получим формулу
для вычисления криволинейного интеграла
при параметрическом задании кривой:
.
(5.10)
Определение криволинейного интеграла 1-го рода, сформулированные выше для плоской кривой, дословно переносятся на случай функции f (x,y,z), заданной вдоль пространственной кривой l. Если эта кривая задана параметрически уравнениями
x = x(t), y =y(t), z = z(t) , , (5.11)
то криволинейный интеграл 1-го рода, взятый вдоль пространственной кривой, вычисляется по формуле
(5.12)
(напомним,
что для кривой (5.11) её дифференциал длины
дуги
).
В случае пространственной кривой (5.11) формула её массы имеет вид
(μ – плотность массы кривой)
,
(5.13)
а координаты центра тяжести С определяются формулами:
;
;
.
(5.14)
Моменты инерции относительно осей X, Y, Z и начала координат 0 для пространственной кривой вычисляются по формулам:
;
;
(5.15)
.
Ясно,
что 2I0
=Ix
+ Iy
+ Iz,
т.е.
.
Кроме того, для пространственной кривой l вводятся моменты инерции относительно координатных плоскостей XY, YZ, ZX. Они определяются формулами:
;
;
.
(5.16)
Отсюда и (5.15) вытекает, что:
.
(5.17)
Плоская
кривая может быть задана в полярных
координатах равенством ρ
= ρ(φ),
α ≤ φ ≤ β.
Так как x
=ρcosφ,
y
= ρsinφ
и
φ)
dφ,
то нетрудно теперь получить формулу
для вычисления криволинейного интеграла
1-го рода в случае задания кривой в
полярной системе координат:
φ,
ρsinφ)
dφ
. (5.18)
Приведем теперь примеры вычисления криволинейных интегралов 1-го рода.
Пример 5.5. Вычислить криволинейный интеграл 1-го рода І вдоль кривой l:
а)
l
– дуга параболы
,
соединяющая
точки (1,
)
и (2, 2);
б)
,
l
– первый
виток конической винтовой линии
x
=tcos
t, y= tsin
t, z = t 0 ≤ t≤ 2π;
в)
,
l
– кривая с
уравнением
;
г*)
,
l
- линия
пересечения поверхностей x²
+ y²
= z²,
y²
= аx,
пробегаемая от точки (0, 0, 0) до точки (0,
a,
а
).
∆ а)
Имеем:
,
,
1 ≤ x
≤ 2.
По формуле (5.9) получаем:
.
б)
Находим
Тогда
.
в) В полярных координатах (x = ρcosφ, y = ρsinφ) уравнение l имеет вид
ρ²
= a²cos2φ,
где
.
Так
как
= ρ
= а²cos2φ,
то по формуле (5.18)
г)
В качестве параметра возьмем x
= t.
Тогда кривая l
задается параметрически равенствами
z = t,
,
,
0 ≤ t
≤ а. Так как
,
то формуле (5.12) получаем
.
Применив к этому интегралу одну из подстановок Эйлера (вычисление интеграла от функции квадратного трехчлена) получаем
.▲