2. Переход от прямоугольных декартовых координат к полярным в двойном интеграле

В тех случаях, когда область интегрирования G ограничена дугами окружностей и (или) лучами, вычисление двойного интеграла существенно упрощается, если перейти от прямоугольной декартовой системы координат к полярной.

Постановка задачи:

Дан интеграл , в котором необходимо перейти от декартовых к полярным.

Получить формулу, позволяющую это сделать.

Наложим прямоугольную декартовую систему координат XOY на полярную систему так, чтобы начала и той, и другой системы совпали, а полярная ось совпала с осью Ox.

Предположим, существует . Это означает, что область G можно разбить на n частей произвольной сетью кривых. В качестве этой сети возьмем координатные линии полярной системы координат: концентрические окружности и лучи .

Найдем площадь элементарной области , используя формулу для площади сектора ( - центральный угол сектора в радианах).

Площадь находится как разность между площадями секторов с радиусами и

и углом .

.

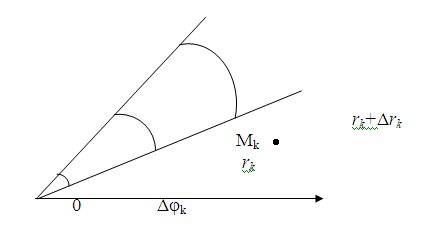
Обозначим 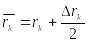. Рассмотрим точку М_k с координатами В прямоугольной декартовой системе координат М_k имеет координаты

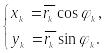
Составим сумму следующего вида:

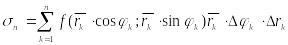
- это интегральная сумма, составленная для области G с разбиением , промежуточными точками М_k , и функции .

Так как по условию интеграл существует, то при

.

Таким образом, получено выражение для двойного интеграла, заданного в прямоугольной декартовой системе в виде равного ему двойного интеграла в полярной системе координат:

= .

Число r характеризует коэффициент деформации бесконечно малой площади dS при переходе от элементарного прямоугольника площадью dxdy в прямоугольной системе координат к элементарному усеченному сектору площадью в полярной системе координат.

Пример:

Вычислить двойной интеграл 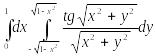, используя полярные координаты.

Область интегрирования G является половиной круга

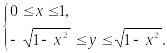
Перейдем к полярным координатам 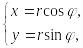при этом в области G , .

Тогда

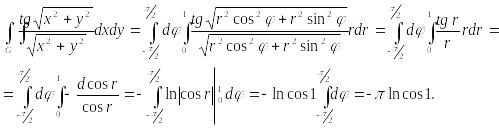
§4. Цилиндрические и сферические координаты

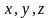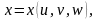
Пусть переход от переменных к новым переменным , осуществляется по формулам где функции 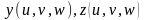непрерывны вместе со своими частными производными первого порядка и устанавливают взаимно однозначное и в обе стороны непрерывное соответствие между точками области 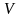пространства 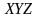и точками некоторой области пространства . Пусть, далее якобиан в области не обращается в нуль:

(4.1)

Тогда пользуются формулой

. (4.2)

В частности, при переходе от декартовых координат к цилиндрическим координатам (рис. 4.1), связанным с соотношениями

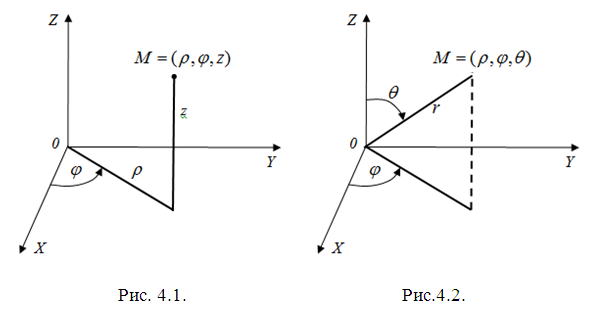
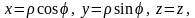(4.3)

или якобиан преобразования (4.3), согласно формуле (4.1) равен . Тогда, согласно (4.2), формула преобразования тройного интеграла к цилиндрическим координатам имеет вид

(4.4)

Заметим, что в ЦСК Далее, согласно (4.4), формулы и для объема тела и его массы с плотностью в ЦСК принимают вид соответственно :

(4.5)

, (4.6)

где - образ области при преобразовании (4.4).

При переходе от декартовых координат к сферическим координатам 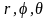(ССК), связанным с соотношениями

(4.7)

или 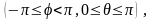модуль якобиана преобразования (4.7), согласно формуле (4.1) 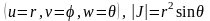. Тогда, согласно (4.2) формула преобразования тройного интеграла к сферическим координатам имеет вид

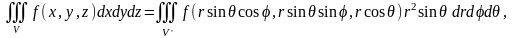(4.8)

где - образ области при преобразовании (4.7).

В ССК Далее, согласно (4.4), формулы для объема тела и его массы с плотностью в ССК принимают вид соответственно:

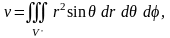(4.9)

(4.10)

где, по прежнему, - образ области при преобразовании (4.7).

1.21. Расставить пределы интегрирования в тройном интеграле

:

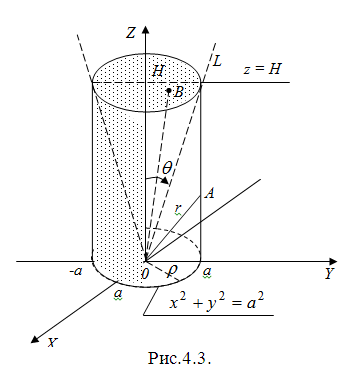
а) в ПДСК; б) в ЦСК; в) в ССК, если - цилиндр, ограниченный поверхностями (рис.4.3).

 а) В ПДСК задача решается наиболее просто:

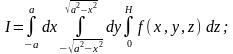
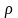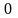б) В ЦСК угловая координата  изменяется, очевидно, от 0 до 2 , полярная координата в круге изменяется от до . Координата в ЦСК имеет тот же смысл, что и в ПДСК. Поэтому в данном цилиндре изменяется от до . Таким образом, в ЦСК, в силу формулы (4.6),

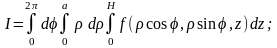в) В ССК одним интегралом не удастся обойтись, ибо луч на поверхности цилиндра разделяет точки 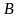, лежащие на поверхности , от точек 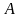, лежащих на боковой поверхности цилиндра. Уравнение поверхности в ССК, согласно (4.7), имеет вид . Уравнение боковой поверхности цилиндра 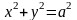в ССК, согласно(4.7) принимает вид

.

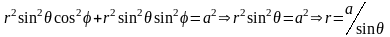Для точек поверхности угол 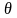очевидно изменяется в пределах от до , а для точек боковой поверхности координата изменяется от до . Координата в обоих случаях изменяется от 0 до 2.

Таким образом, согласно (4.8), имеем

