
- •Часть 3
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Правила оформления
- •Рабочая учебная программа
- •Часть 2 254
- •Часть 3 102
- •Часть 4 152
- •Пояснительная записка
- •1. Контрольные работы
- •2. Учебно-методические материалы по дисциплине
- •3. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов и технических средств обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Теоретический раздел Глава 1. Дифференциальные уравнения и системы дифференциальных уравнений. Элементы теории устойчивости
- •§1. Основные понятия теории дифференциальных уравнений
- •§2. Дифференциальные уравнения 1-го порядка, интегрируемые в квадратурах
- •II. Дифференциальные уравнения с разделяющимися переменными
- •III. Дифференциальные уравнения с однородными функциями
- •V. Уравнения Бернулли
- •VI. Дифференциальные уравнения, обладающие интегрирующими множителями, зависящими от одной переменной.
- •§3. Дифференциальные уравнения высших порядков
- •§4. Линейные дифференциальные уравнения n-го порядка
- •§5. Линейные неоднородные дифференциальные уравнения (лнду) с произвольными коэффициентами
- •§6. Системы дифференциальных уравнений
- •Метод исключения.
- •Метод интегрируемых комбинаций
- •§7. Введение в теорию устойчивости
- •§8. Устойчивость по Ляпунову
- •§9. Классификация точек покоя однородной системы двух линейных дифференциальных уравнений первого порядка с постоянными действительными коэффициентами
- •§10. Исследование на устойчивость решений нелинейных систем. Устойчивость по первому приближению
- •Глава 2. Кратные, криволинейные и поверхностные интегралы. Теория поля (ж.А.Черняк, а.А. Карпук, в.А. Ранцевич) §1. Двойной интеграл. Определение и свойства
- •§2. Тройной интеграл
- •§3. Вычисление кратных интегралов в прямоугольной декартовой системе координат
- •Переход от прямоугольных декартовых координат к полярным в двойном интеграле
- •§4. Цилиндрические и сферические координаты
- •§5. Криволинейные интегралы 1-го рода
- •§6. Криволинейные интегралы 2-го рода
- •§7. Поверхностный интеграл 1-го рода (пи-1)
- •§8. Поверхностный интеграл второго рода
- •§9. Элементы теории поля и векторного анализа
- •1. Оператор Гамильтона (набла)
- •Глава 3. Числовые и функциональные ряды
- •§1. Числовые ряды. Основные определения и понятия
- •§2. Признаки сходимости положительных рядов
- •§3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§4. Функциональные ряды
- •§5. Равномерная сходимость функционального ряда. Основные свойства равномерно сходящихся рядов
- •§6. Степенные ряды
- •§7. Разложение функции в степенной ряд. Ряд Тейлора
- •§8. Приложения степенных рядов
- •Методические указания к выполнению контрольной работы 7
- •Тесты для самопроверки
- •Контрольная работа 8. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 8
- •Тесты для самопроверки
- •Контрольная работа 9. Ряды. Указания к выбору варианта
- •Задания
- •Методические указания к выполнению контрольной работы 9
- •Тесты для самопроверки
- •Радикальный признак Коши.
- •Интегральный признак Коши.
- •6. Знакочередующие ряды. Признак Лейбница. Знакопеременные ряды.
- •8. Применение степенных рядов.
§3. Вычисление кратных интегралов в прямоугольной декартовой системе координат
3.1. Вычисление двойного интеграла в прямоугольной декартовой системе координат.
Определение:
Область
назовем выпуклой вдоль оси
![]() ,
если она задается системой неравенств
,
если она задается системой неравенств
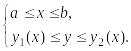
Область
является выпуклой вдоль оси
,
тогда и только тогда, когда любая прямая
![]() (параллельная оси
),
где
(параллельная оси
),
где
![]() ,
пересекает границы области не более
чем в двух точках.
,
пересекает границы области не более
чем в двух точках.
При
этом линия
![]() с уравнением
с уравнением
![]() называется линией
входа в область
,
а линия
называется линией
входа в область
,
а линия![]() с уравнением
с уравнением
![]() называется
линией выхода
из области
называется
линией выхода
из области
![]()

Аналогично
определяется область, выпуклая вдоль
оси
![]() .
.
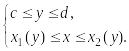
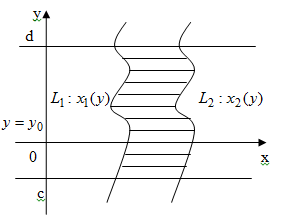
Теорема 3.1 (о сведении двойного интеграла по выпуклой вдоль оси ОY области к повторному).
Пусть функция интегрируема по области , выпуклой вдоль оси
![]()
Если
для любой точки
![]() ,
принадлежащей интервалу
,
принадлежащей интервалу
![]() ,
существует интеграл
,
существует интеграл
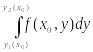 ,
,
то справедлива формула сведения двойного интеграла к повторному:
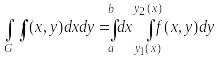 (3.1)
(3.1)
Интеграл справа в формуле (3.1) называется повторным интегралом и вычисляется изнутри, то есть сначала вычисляется интеграл по при фиксированном значении , а затем вычисляется внешний интеграл по переменной .
Доказательство:
Приведем геометрическое доказательство формулы (3.1).
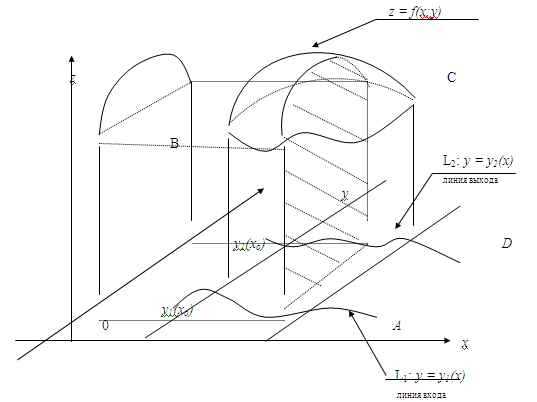
z = f(x;y)
Для
простоты доказательства будем считать,
что
![]() .
.
Тогда, с одной стороны, двойной интеграл равен объему цилиндрического бруса, т.е.
![]() .
.
С
другой стороны, по условиям теоремы для
любого
![]() из
интервала
из
интервала
![]() существует
существует
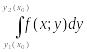 .
.
Выясним
геометрический смысл последнего
интеграла. Произведем сечение
цилиндрического бруса плоскостью
![]() .
В сечении получим криволинейную трапецию
ABCD.
.
В сечении получим криволинейную трапецию
ABCD.
Очевидно, что площадь SABCD этой трапеции численно равна
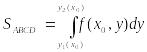 .
.
Поскольку аналогичные рассуждения справедливы для любого из интервала , то функция
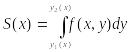
выражает площадь поперечного сечения цилиндрического бруса плоскостями, перпендикулярными оси Ox.
Поэтому объем цилиндрического бруса можно вычислить и другим способом, используя формулу:
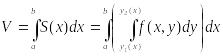 .
.
Сравнивая два полученных выражения для объема цилиндрического бруса, приходим к окончательному результату:
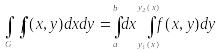 .
.
Замечание:
Если область G выпукла вдоль оси Ox, то справедлива формула, аналогичная формуле(3.1)
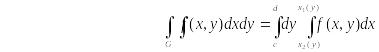 (3.2)
(3.2)
где
область G
задана системой неравенств
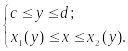
Если область G не является выпуклой вдоль осей Ox и Oy , то её нужно разбить на конечное число частей
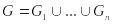 ,
не имеющих общих внутренних точек,
выпуклых вдоль какой-либо оси.
,
не имеющих общих внутренних точек,
выпуклых вдоль какой-либо оси.
Легко заметить, что в повторных интегралах из формул (3.1) и (3.2) внешние пределы интегрирования всегда являются константами, а пределы интегрирования внутреннего интеграла в общем случае являются функциями, зависящими от той переменной, по которой вычисляется внешний интеграл.
В повторных интегралах из формул (3.1) и (3.2) и внешние, и внутренние пределы интегрирования являются константами в том и только в том случае, когда областью интегрирования G является прямоугольник.
Например,
областью интегрирования повторного
интеграла
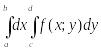 является
прямоугольник G:
является
прямоугольник G:
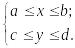
Пример вычисления двойного интеграла с помощью сведения к повторному.
Расставить пределы интегрирования и вычислить двойной интеграл
![]() по
области G,
заданной системой неравенств
по
области G,
заданной системой неравенств
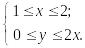
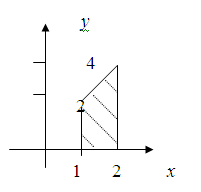
Поскольку область интегрирования G является выпуклой как вдоль оси Oy, так и вдоль оси Ox, то исходный двойной интеграл можно записать одним из следующих способов:
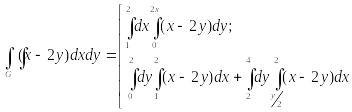
Вычислим двойной интеграл, используя его первое представление в виде повторного:
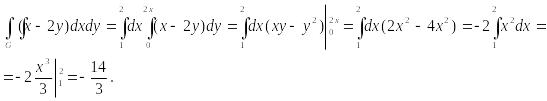
Вычисление тройного интеграла в прямоугольной декартовой системе координат
Пусть
Т
– компакт пространства
,
функция
 – отображение компакта Т
во множество R.
– отображение компакта Т
во множество R.
Предположим,
существует тройной интеграл вида
![]() .
.
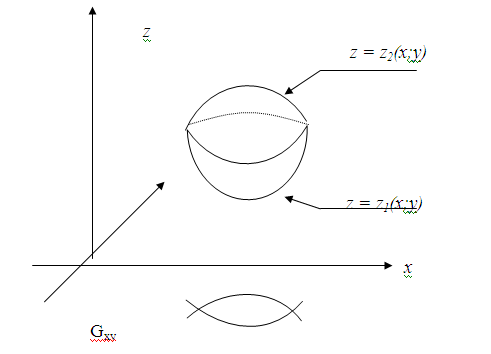
Будем
рассматривать тело Т
, выпуклое вдоль оси Oz.
Пусть Т
ограничено снизу и сверху поверхностями
с уравнениями
![]() и
и
![]() соответственно,
Gxy
– проекция тела Т
на плоскость
XOY.
соответственно,
Gxy
– проекция тела Т
на плоскость
XOY.
Геометрически
выпуклость тела Т
относительно оси Oz
означает, что любая вертикальная прямая
с уравнением
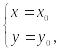 где
где
![]() – внутренняя точка области G,
пересекает границы тела Т
не более чем в двух точках.
– внутренняя точка области G,
пересекает границы тела Т
не более чем в двух точках.
В этом случае можно получить формулу сведения тройного интеграла к следующему повторному интегралу:
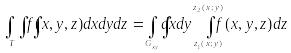 .
.
Если
теперь область Gxy
выпукла вдоль оси Oy,
т.е. определяется неравенствами
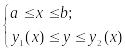 ,
то двойной интеграл
,
то двойной интеграл
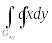 может быть выражен через повторный по
формуле (3.1)
может быть выражен через повторный по
формуле (3.1)
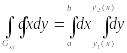 .
.
Тогда исходный тройной интеграл будет окончательно представлен в виде трехкратного (или повторного ) интеграла по формуле
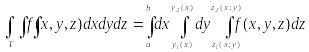 .
(3.3)
.
(3.3)
