§2. Тройной интеграл

Пусть в пространстве задан компакт , в каждой точке которого определена функция .

Определение тройного интеграла.

Рассмотрим алгоритм, состоящий из следующих четырех шагов:

1. Разобьем тело произвольным образом на частей так, что 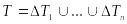; 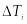и 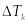не имеют общих внутренних точек, .

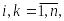
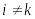Пусть объем элементарного тела (тело предполагается кубируемым, то есть имеющим объем), диаметр тела , то есть ,

2. В каждой элементарной области выберем произвольную точку 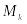и вычислим значение функции 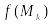в соответствующей точке .

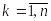3. Составим интегральную сумму для функции по области

.

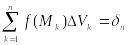Пусть ∆ максимальный среди всех диаметр разбиения.

4. Если существует конечный предел интегральной суммы 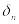, который не зависит ни от способа разбиения тела , ни от выбора промежуточных точек , тогда этот предел называется тройным интегралом от функции по области и обозначается

,

где подынтегральная функция,

знак тройного интеграла,

дифференциал объема,

область интегрирования.

В прямоугольной декартовой системе координат тройной интеграл записывается в виде где

Геометрический и механический смысл тройного интеграла.

Пусть подынтегральная функция в области . Тогда

- объем тела , значит, .

Физический смысл тройного интеграла.

Пусть – компакт в пространстве , в котором задана функция , являющаяся плотностью распространения масс в компакте ,

тогда

.

Теорема 2.1 (о существовании тройного интеграла).

Пусть функция непрерывна на компакте пространства , причем тело ограничено кусочно-гладкими поверхностями. Тогда функция интегрируема на области , то есть существует тройной интеграл: .

Основные свойства двойных и тройных интегралов без изменения повторяют свойства определенных интегралов, причем доказываются они аналогичными методами. Приведем основные свойства кратных интегралов на примере свойств двойных интегралов.

Основные свойства двойных интегралов.

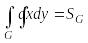, где - площадь области

Линейность.

Пусть функции и интегрируемы на области , тогда для любых чисел функция тоже интегрируема по области . При этом справедлива следующая формула:

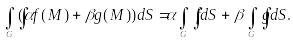
Аддитивность интеграла.

Если функция интегрируема на области , а область является объединением двух областей и , не имеющих общих внутренних точек, тогда справедлива формула

.

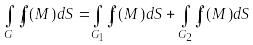Монотонность интеграла.

Если функции и интегрируемы на области , причем для любой точки из области , тогда

.

В частности, если функция , для любой точки из области , то .

Если функция интегрируема на области , причем для любой точки из области выполняется неравенство , тогда

.

Оценка модуля двойного интеграла.

Если функция интегрируема на области , то и функция интегрируема на области , при этом справедливо следующее неравенство:

.

Теорема о среднем.

Пусть функция непрерывна на связном компакте (множество называется связным, если любые две его точки можно соединить непрерывной кривой, целиком содержащейся в этом множестве), тогда существует такая точка из области , что

.