§10. Исследование на устойчивость решений нелинейных систем. Устойчивость по первому приближению

В данном параграфе рассмотрим некоторые методы исследования на устойчивость нелинейных систем дифференциальных уравнений.

Пусть дана автономная система дифференциальных уравнений.

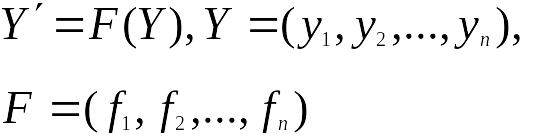(10)

Правые части системы (10) не являются линейными функциями.

Не нарушая общности будем считать, что y=0 есть точка покоя системы.

Разложим правые части системы, т.е. функции f_i по формуле Маклорена в окрестности точки покоя.

Тогда система примет вид:

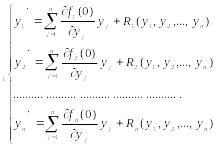(11)

Если отбросить нелинейные слагаемые в (11), то получим линейную систему с постоянными коэффициентами, которая называется системой первого приближения (или линеаризованной системой).

Устойчивость точки покоя исходной системы (10)определяется по устойчивости этой точки для линеаризованной системы.

Теорема Ляпунова. 10.1 Точка покоя нелинейной системы (10) асимптотически устойчива (неустойчива), если асимптотически устойчива (неустойчива) точка покоя линейной системы первого приближения.

Пример 3. Исследовать на устойчивость точки покоя системы .

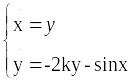Решение.

1. Найдем точки покоя данной системы

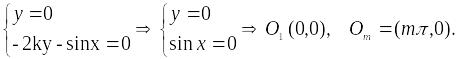
2. Линеаризуем систему в окрестности первой особой точки (0,0):

.

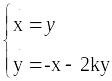Корни характеристического уравнения имеют вид

3. Если k>0 , то точка (0,0) будет асимптотически устойчивой

( узлом или фокусом) .

Если k<0 , то неустойчива.

3. Согласно теоремы 4.1 точка покоя (0,0) будет сохранять свой тип и для исходной системы.

4. Линеаризуем систему в окрестности первой особой точки ( 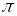,0):

.

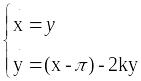Корни характеристического уравнения имеют вид Анализ корней показывает, что они всегда разных знаков, следовательно данная точка является неустойчивой и для исходной системы.

Если же точка покоя линейной системы является центром, т. е. устойчива, то для нелинейной системы она может быть или центром или фокусом. Требуются дополнительные исследования.

Заметим, что в этом случае характеристические корни будут чисто мнимыми.

Для автономных систем верна теорема.

Теорема 10.2(об устойчивости). Если существует дифференцируемая функция , удовлетворяющая в окрестности начала координат следующим условиям:

1.

2. ,

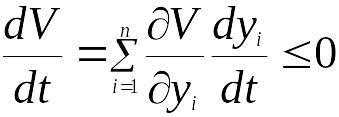то точка покоя системы устойчива.

Теорема 10.3(об асимптотической устойчивости) .Если существует дифференцируемая функция , удовлетворяющая в окрестности начала координат следующим условиям:

1.

2. ,

причем

3.

то точка покоя системы асимптотически устойчива.

Теорема 10.4(о неустойчивости). Если существует дифференцируемая функция , удовлетворяющая в окрестности начала координат следующим условиям:

1.

2. ,

причем

3.

то точка покоя системы неустойчива.

Общего метода построения функции Ляпунова нет. В каждом конкретном случае ее подбирают исходя из вида системы.

Это могут быть функции ,

или

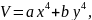
где коэффициенты а,b - положительные числа.

Пример 4. Исследовать на устойчивость точки покоя системы 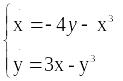Решение.

1. Найдем точки покоя:

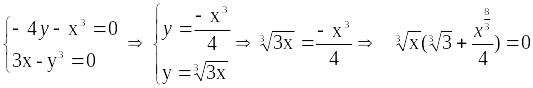
из

последнего равенства следует, что единственным решением является х=0, у=0.

2.Собственные числа для линеаризованной системы в окрестности точки (0,0)

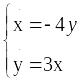находим из уравнения

Особая точка для данной системы является центром и следовательно она устойчива, тогда теорема 4.1 не распространяется и вопрос о классификации точки (0,0) для исходной системы попытаемся решить с помощью функции Ляпунова.

2. Построим функцию Ляпунова вида где а >0 и b >0.

3. Найдем

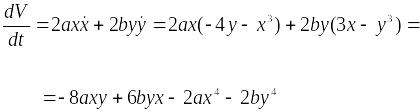
Чтобы нужно получить выполнение равенства , которое выполняется при . Тогда при а=1

, а следовательно функция Ляпунова .

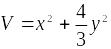Данная функция удовлетворяет условиям теоремы 4.3 , что означает асимптотическую устойчивость точки покоя (0,0) для исходной системы.

Литература.

1. Жевняк P.M., Карпук А.А. Высшая математика./Дифференциальные уравнения. Ряды. Уравнения магматической физики. Теория функций комплексной переменной/.- Мн.: ИРС '''Образование", 1997. - 572 с.

2. Краснов М.Л., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновенным дифференциальным уравнениям: Учебн. пособие для втузов. – М.: Высш. школа, 1978. – 287с., ил.

3. Понтрягин Л.С. Дифференциальные уравнения и их приложения. Москва.: Наука, 1988. 208с.