§8. Устойчивость по Ляпунову

Пусть задана система уравнений:

(1)

с начальными данными .

Пусть - решение системы (1).

Определение1. Решение называется устойчивым по Ляпунову, если для любого ε>0 существует δ>0, что для любого другого решения той же системы , начальные значения которого удовлетворяет неравенствам: , i=1,2,….,n справедливы неравенства , ( i=1,2,…..,n) при любом значении .

Таким образом, решение устойчиво по Ляпунову, если близкие к нему значения по начальным условиям решения остаются близкими (рис.1) и для всех

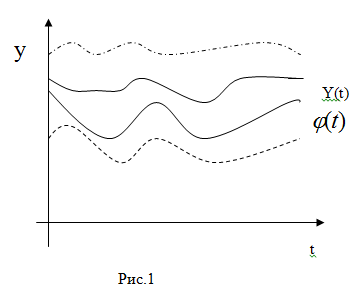
Определение2. Если решение устойчиво по Ляпунову и выполняется равенство ( i=1,2,…..,n), то решение называется асимптотически устойчивым.

Примечание: Из асимптотической устойчивости не следует устойчивость по Ляпунову.

Исследование на устойчивость по Ляпунову произвольного решения системы (1) можно свести к исследованию на устойчивость нулевого (тривиального ) решения некоторой другой системы, полученной из исходной путем замены вида , i=1,2,…..,n.

Тогда .

Подставим полученное выражение в систему (1) :

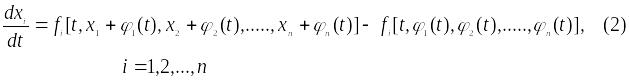
Система (2) имеет тривиальное решение , i=1,2,…,n.

Для системы (2) справедлива теорема:

Теорема 8.1. Решение системы (1) устойчиво по Ляпунову (асимптотически устойчиво) тогда и только тогда, когда устойчиво по Ляпунову (асимптотически устойчиво) тривиальное решение системы (2).

Тривиальное решение обладает тем свойством, что оно не изменяется при изменении t, т.е. стоит на месте.

Определение3. Тривиальное решение ( i=1,2,…,n) называется устойчивым по Ляпунову, если для любого ε>0 существует >0, что из неравенства (i=1,2,…,n )следует неравенство (i=1,2,…,n) при любом значении .

Это означает, что если траектория, начальная точка которой (условия задачи Коши) расположена в -окрестности начала координат, то и при изменении t она не выходит за пределы -окрестности этой точки .

Замечание. Произвольное частное решение y=y(t) линейной неоднородной системы дифференциальных уравнений , записанной в векторной форме

(3)

будет устойчивым по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение соответствующей однородной системы

(4)

Таким образом, целесообразно изучить вначале устойчивость решений систем вида (4).

В данной главе рассматриваются вопросы устойчивости положений равновесия автономных систем, т.е. в своей записи не содержащих явно независимую переменную, в нашем случае переменную t.

§9. Классификация точек покоя однородной системы двух линейных дифференциальных уравнений первого порядка с постоянными действительными коэффициентами

Рассмотрим систему 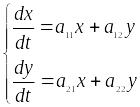(5)

где матрица - матрица коэффициентов содержит только действительные числа, -столбец искомого решения.

В смысле введенных обозначений система (5) может быть записана

(6)

Определение4.Точкой покоя такой системы (6)называется точка , в которой правые части системы обращаются в ноль, т.е. это решение однородной алгебраической системы вида

(7)

Очевидно, что данная система всегда будет иметь тривиальное решение (х,у)=(0,0). Если определитель матрицы 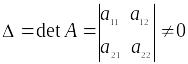, то тривиальное решение будет единственным . Если 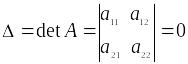, тогда система (7) будет иметь и другие , нетривиальные решения . Однако с помощью преобразования координат (параллельный перенос) можно всегда придти к точке (0,0).

Из опыта решения линейных систем дифференциальных уравнений известно, что вначале находят корни характеристического уравнения

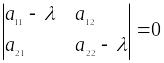Или . (8)

Если , то характеристические корни системы не будут нулевыми. Корни зависят от коэффициентов системы и могут принимать различные значения как действительные, так и мнимые.

Характеристические корни системы называют еще собственными значениями.

Рассмотрим все возможные случаи и определим роль знаков собственных значений в вопросе устойчивости тривиального решения:

1.Пусть корни характеристического уравнения (8) λ1и λ2действительны , различны и одинаковых знаков.

Пусть им соответствуют собственные векторы матрицы А и

Тогда, как известно, общее решение системы примет вид:

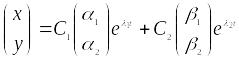, (9)

где - произвольные постоянные.

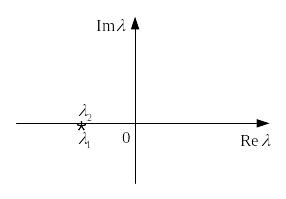
Если λ1<0 и λ2<0, то из (9) видно, что точка покоя х=у=0 является асимптотически устойчивой.

Пример 1: Исследовать на устойчивость точку покоя системы.

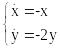
1. Характеристические корни λ1 = -1; λ2 = -2 .

2. Собственные векторы

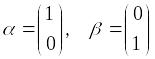
3. Общее решение или

4. Решение задачи Коши

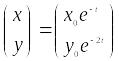
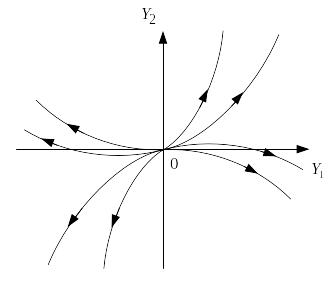
5. Исключим параметр t и получим функцию 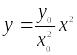, графиком которой является парабола. При изменении начальных условий получим семейство парабол как на рис.2.

Точка покоя, у которой собственные числа различны и отрицательны, называется устойчивым узлом.

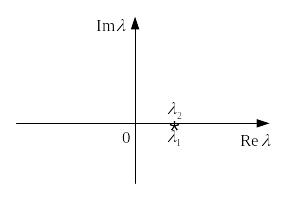
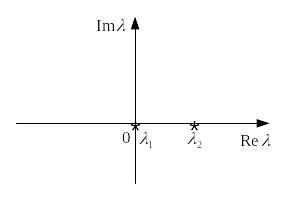
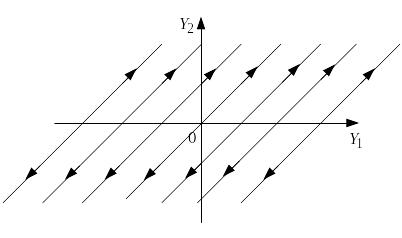
Если λ1>0 и λ2>0, то из (9) видно , что точка покоя х=у=0 является неустойчивой так как при . Траектории удаляются от точки покоя. Точка (0,0) называется неустойчивым узлом (рис3).

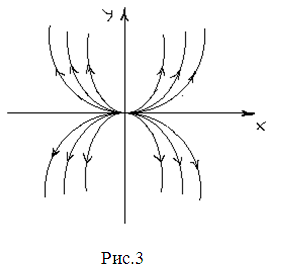
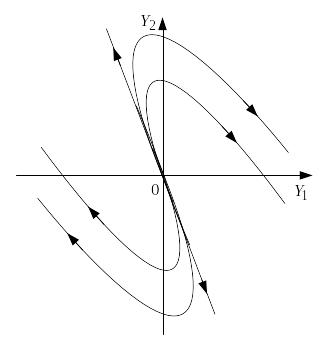
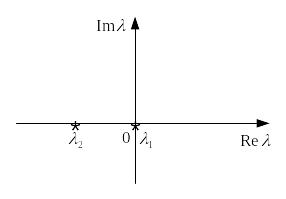
2.Корни характеристического уравнения (8) λ1и λ2 действительны , различны и разных знаков ( λ1>0, λ2 < 0).

В этом случае при , а . Точка покоя будет неустойчивой и называется седлом. Топологический портрет изображен на рис. 4.

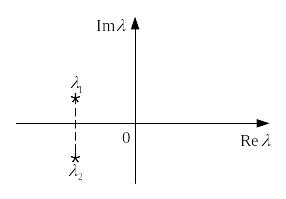
3.Корни характеристического уравнения (8) λ1и λ2комплексно – сопряженные.

Пусть .

Решение системы можно записать в виде:

= е ;

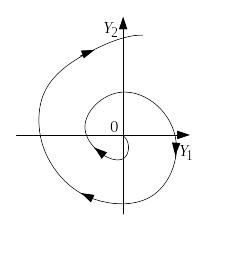
Анализ решения показывает, если р < 0, то при t → +∞ траектории стремятся к точке покоя (рис.5) . Такая точка покоя называется устойчивым фокусом.

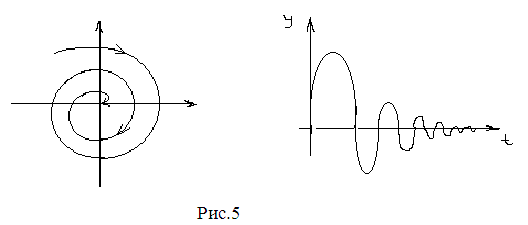
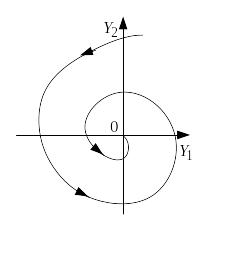
Если р> 0, то при t → +∞ траектории раскручиваются , удаляясь от точки покоя, которая в этом случае называется неустойчивым фокусом (рис.6).

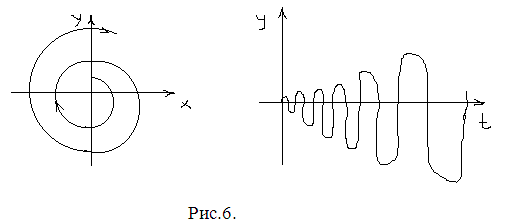
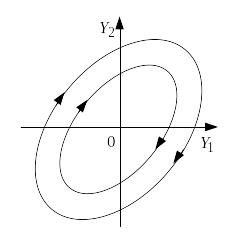
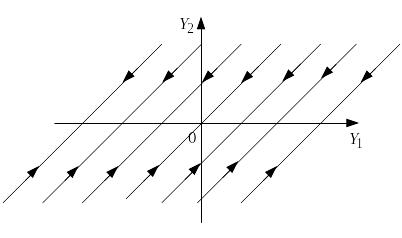
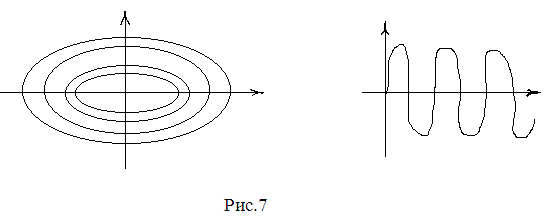
Если р = 0, то решение системы будут периодическими функциями

х = А×sin(qt+φ1);

y = B×sin(qt+φ2) периода , т.е. на фазовой плоскости это замкнутые кривые (рис.7), расположенные вокруг точки покоя (0;0), которая называется центром. Центр является устойчивой точкой, но не асимптотически устойчивой.

Пример 2: Провести исследование решений уравнения, описывающего работу линейного осциллятора , в зависимости от параметров b и c:

1)Переход к системе:

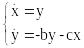
2)Решение характеристического уравнения:

3) Анализ знаков корней характеристического уравнения в зависимости от знаков параметров в (ось ординат) и с (ось абсцисс) и изображение фазовых портретов траекторий на плоскости параметров в и с приведен на рис.8. Парабола соответствует уравнению

Таблица видов простейших точек покоя

Точка покоя	Собственный значения	Фазовые траектории
Неустойчивый узел
Устойчивый узел
Седло
Устойчивый узел	(Один собственный вектор)
Неустойчивый узел	(Один собственный вектор)
Дикритичес-кий узел	(Два собственных различных вектора)
Центр
Неустойчивая
Устойчивая
Неустойчивый фокус
Устойчивый фокус