Метод исключения.
Метод исключения основан на двух утверждениях (6.2 и 6.3).
Утверждение 6.2.
Любое
дифференциальное уравнение
-
го порядка
эквивалентно нормальной системе
дифференциальных уравнений.
Доказательство.
Пусть дано уравнение
.
Обозначим
(*)
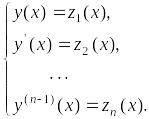Тогда
очевидны следующие соотношения,
связывающие функции
:
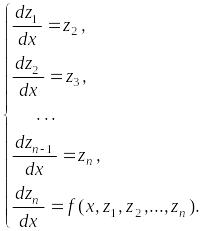
Покажем, что полученная нормальная система и исходное уравнение эквивалентны.
Если
– решение исходного дифференциального
уравнения, то система обозначений (*)
позволяет найти решение нормальной
системы
.
И наоборот, если известно решение системы
,
то
– решение исходного дифференциального
уравнения, т.е. уравнение и полученная
из него система эквивалентны, что и
требовалось доказать.
Следующее утверждение содержит в своем доказательстве алгоритм метода исключения для решения нормальной системы.
Утверждение 6.3.
Если дана нормальная система (6.2), то при определенных условиях она эквивалентна одному дифференциальному уравнению - го порядка.
Доказательство. Рассмотрим систему (6.2). Продифференцируем повторно любое ее уравнение (для определенности, пусть это будет первое уравнение):
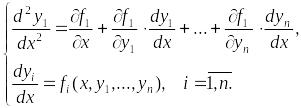
В
новое уравнение системы подставим
.
В результате получим уравнение
.
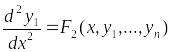Продифференцируем
это уравнение еще раз, при этом снова
заменим
правыми частями уравнений исходной
системы:
.
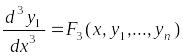Повторяем эту операцию до тех пор, пока не получим уравнение
.
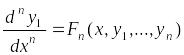В итоге получаем следующую систему уравнений:
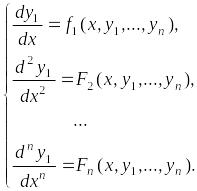
Если
первые
уравнений системы удается разрешить
относительно функций
,
т.е. из этих уравнений удается выразить
(**)
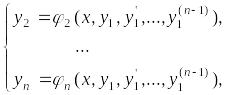то, подставив эти функции в последнее уравнение системы, получим искомое уравнение, эквивалентное исходной системе (6.2).
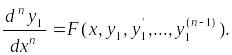(6.5)
Покажем
эквивалентность системы (6.2) и уравнения
(6.5). Пусть
– решение уравнения (6.5), тогда, подставляя
в систему (**), находим остальные неизвестные
функции
.
И наоборот, пусть
– решение исходной системы, тогда
– решение полученного уравнения (6.5).
Пример.
Решить нормальную систему методом исключения.
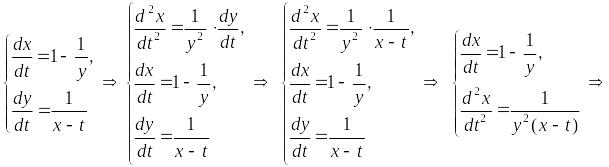
Найдем
неизвестную функцию
,
решая последнее уравнение:
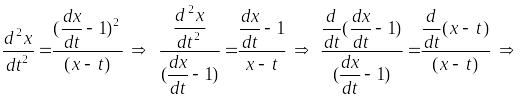
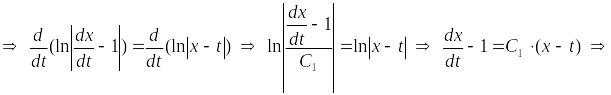
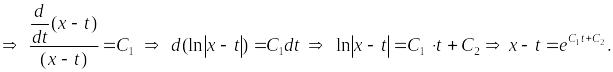
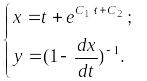
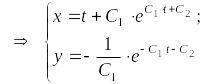– общее
решение системы.
Метод интегрируемых комбинаций
Интегрируемой комбинацией системы (6.2) называется такое следствие уравнений этой системы, которое легко интегрируется.
Рассмотрим этот метод на следующем примере.
Пример.
Решить систему уравнений
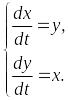
Складывая и вычитая уравнения системы, получаем две интегрируемые комбинации:
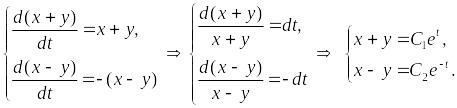
Складывая и вычитая полученные соотношения, окончательно получаем общее решение системы:
.
Для системы (6.2) одна интегрируемая комбинация позволяет получить одно соотношение вида
,
связывающее
независимую переменную
и неизвестные функции
.
Такое соотношение называется первым
интегралом системы (6.2). Точнее:
дифференцируемая функция
,
не равная тождественно постоянной, но
сохраняющая постоянное значение на
любой интегральной кривой этой системы,
называется первым интегралом системы
(6.2).
Если
найдено
первых интегралов системы (6.2) и все они
независимы, т.е. якобиан системы функций
отличен от нуля:
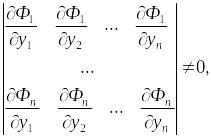
то задача интегрирования системы (6.2) решена, так как из системы
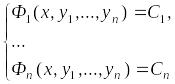
определяются все неизвестные функции .