§6. Системы дифференциальных уравнений

Систему дифференциальных уравнений вида

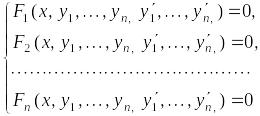(6.1)

будем называть системой дифференциальных уравнений 1-го порядка, при этом – неизвестные функции аргумента ,

– известные функции от переменных.

Упорядоченный набор функций , дифференцируемых на интервале , называется решением системы (6.1) на интервале , если при их подстановке в систему (6.1) она превращается в систему верных тождеств по x на интервале .

Если систему (6.1) удается записать в виде

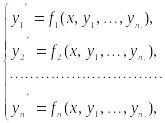(6.2)

то такая система называется нормальной системой дифференциальных уравнений. Очевидно, что система (6.2) является обобщением одного дифференциального уравнения , разрешённого относительно производной.

Все последующие определения и теоремы будут формулироваться для нормальной системы дифференциальных уравнений (6.2).

Рассмотрим, как ставится задача Коши для системы (6.2).

Пусть задана точка , которая определяет систему начальных условий:

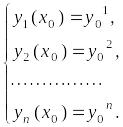(6.3)

Найти такое решение системы (6.2), которое удовлетворяет начальным условиям (6.3) («проходящее» через точку ).

Сформулируем свойство локальной единственности решения (СЛЕР) для системы дифференциальных уравнений (6.2). Пусть – некоторая открытая область пространства . Будем говорить, что в области система (6.2) обладает СЛЕР, если для любой точки существует такая окрестность точки , что через точку всегда «проходит» некоторое решение системы (6.2), единственное в указанном выше интервале .

Теорема 6.1 (Коши).

Пусть в открытой области правые части системы (6.2) удовлетворяют следующим условиям: эти функции непрерывны в области , причём их частные производные по переменным ограничены в . Тогда нормальная система дифференциальных уравнений (6.2) имеет единственное решение для любой точки , т.е. в области система (6.2) обладает СЛЕР.

Определение. Пусть в открытой области система (6.2) обладает СЛЕР, тогда параметрическое семейство функций

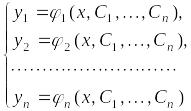(6.4)

называется общим решением системы дифференциальных уравнений (6.2) в области , если выполняются следующие 2 условия.

1. Для любого допустимого набора констант упорядоченный набор функций

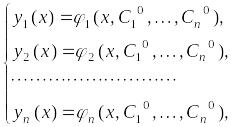
является решением системы (6.2) в области .

2. Для любой точки из области можно однозначно определить числа , для которых набор функций

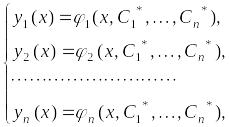
является решением, «проходящим» через точку , т.е. удовлетворяющим задаче Коши с начальными условиями (6.3).

Любое решение, полученное из общего решения (6.4) при подстановке допустимого набора констант , называется частным решением системы дифференциальных уравнений (6.2).

Решение системы (6.2), которое не может быть получено из общего решения ни при каких значениях констант, включая случай , называется особым решением системы дифференциальных уравнений (6.2).

Пример.

Решить систему дифференциальных уравнений:

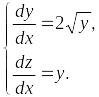
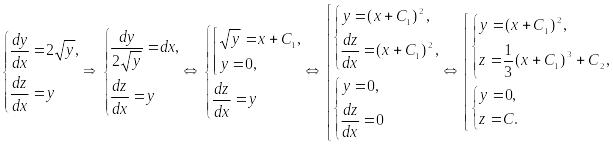
Таким образом – общее решение системы в области

,

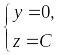– особое решение системы,

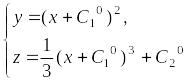– частное решение системы при фиксированных константах .

Для случая нормальная система (6.2) имеет простую механическую интерпретацию. Обозначим независимую переменную буквой и будем называть ее временем, а неизвестные функции – . Тогда система (6.2) примет вид:

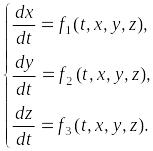
В этом случае система (6.2) называется динамической системой, а ее решения – движениями, т.к. они описывают положение движущейся точки в пространстве в зависимости от времени . Пространство называется фазовым пространством,

а вектор – фазовой скоростью точки.

Методы решения нормальных систем