8.2. Знакочередующиеся ряды

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов

.

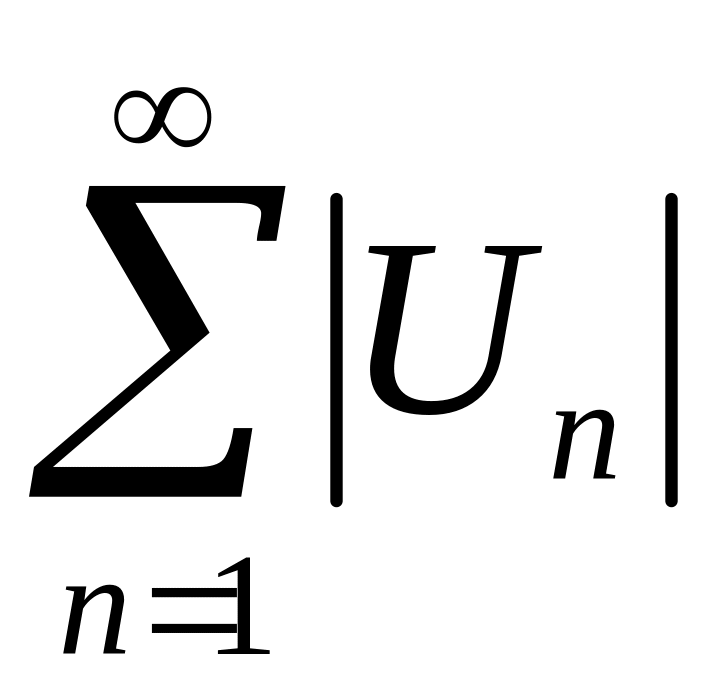Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Знакочередующимся рядом называется ряд вида

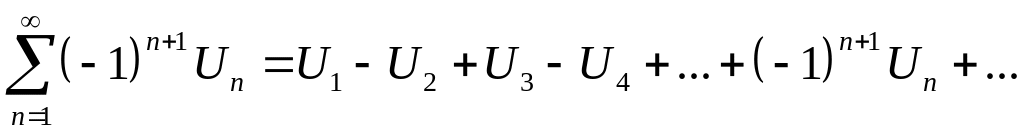
где при ., т.е. ряд, у которого любые рядом стоящие члены его имеют противоположные знаки.

Теорема (признак Лейбница). Пусть в знакочередующемся ряде числовая последовательность убывает, и . Тогда этот ряд сходится (по крайней мере условно), причем его сумма S положительна и не превосходит первого члена: .

Пример

Исследовать на абсолютную и условную сходимость ряд .

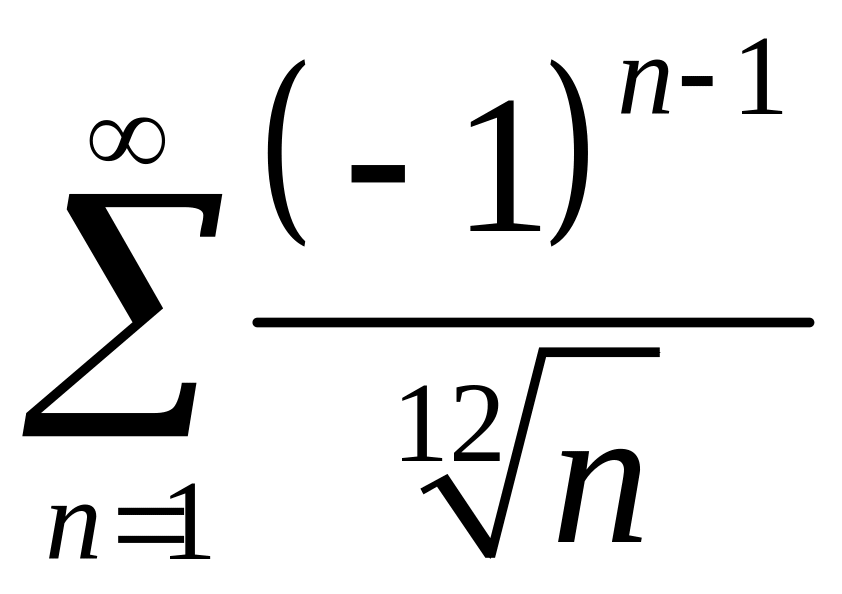Решение

Так как данный ряд – знакочередующийся, то для решения вопроса о его сходимости можно применить признак Лейбница.

Члены ряда убывают по абсолютной величине

,

общий член ряда стремится к нулю при :

.

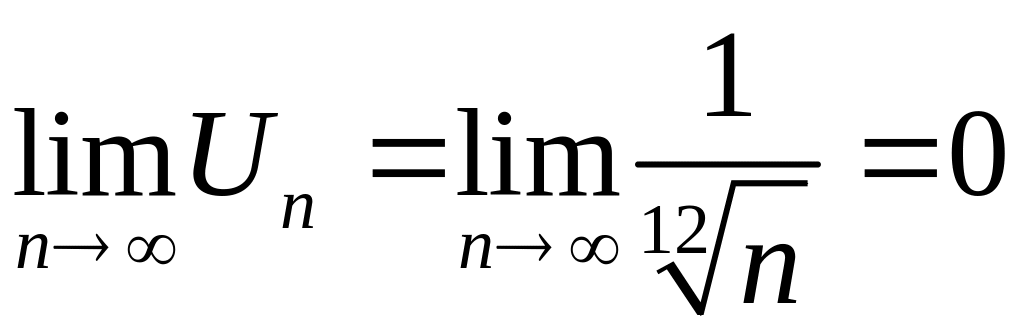Оба условия признака Лейбница выполняются, следовательно, данный ряд сходится.

Чтобы решить вопрос о том, сходится ли ряд абсолютно, составим ряд из абсолютных величин его членов

.

Этот ряд расходится как обобщенный гармонический ряд, в котором , следовательно, абсолютной сходимости нет, данный ряд сходится условно.

8.3. Область сходимости степенного ряда

Степенным рядом называется функциональный ряд вида

.

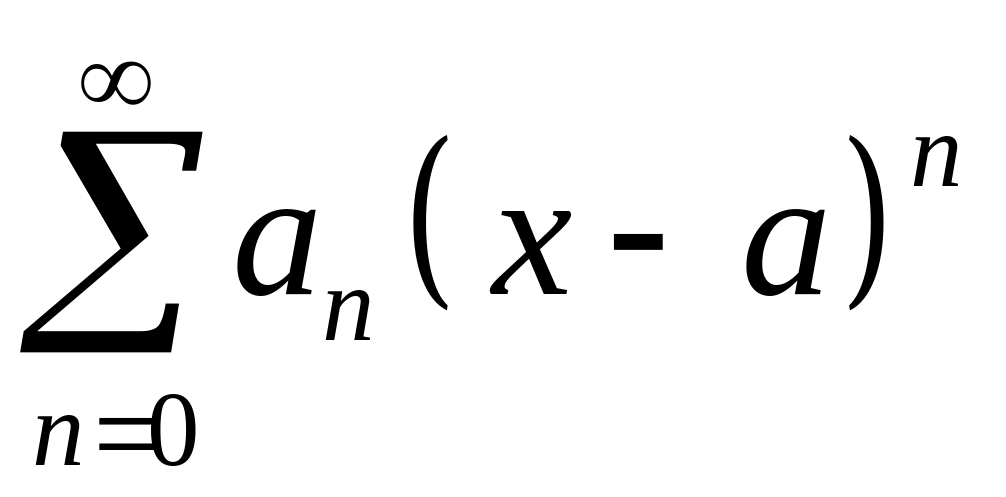где – постоянные величины – коэффициенты степенного ряда, а – число, х – переменная.

Рассматривают, также, степенной ряд вида

.

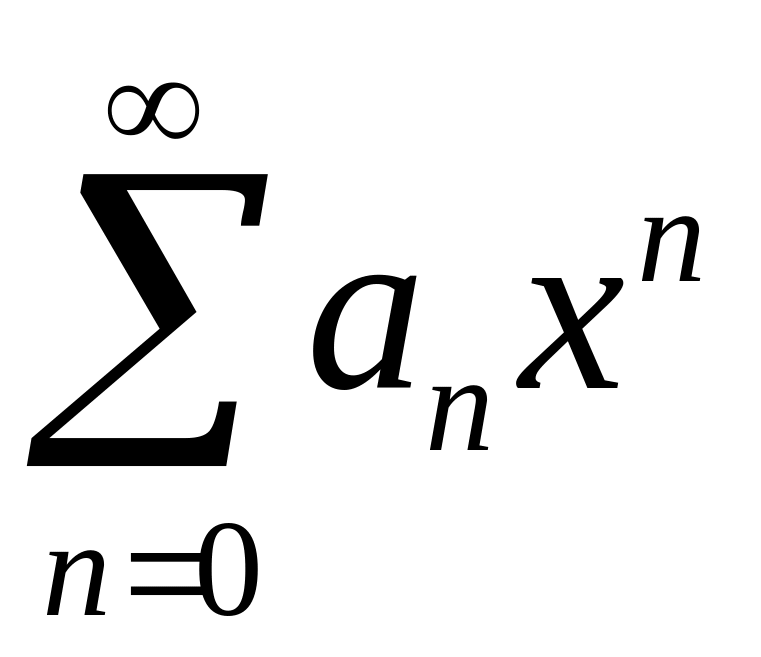Структура области сходимости степенного ряда устанавливается теоремой Абеля.

Теорема Абеля. Если степенной ряд сходится при некотором значении , не равном нулю, то он абсолютно сходится при всяком значении х, для которого . Если ряд расходится при некотором значении , то он расходится при всяком х, для которого .

Из теоремы Абеля следует, что существует число R, для которого при ряд сходится, а при – расходится. Такое число R называется радиусом сходимости степенного ряда .

Интервалом сходимости степенного ряда называется такой интервал от до , что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится.

При вопрос о сходимости ряда остается открытым и решается дополнительно.

При область сходимости – точка . При область сходимости – вся числовая прямая.

Если в точках ряд расходится, то – область сходимости (одновременно интервал сходимости). Если хотя бы в одной точке ряд сходится, то интервал сходимости и область сходимости не одно и то же.

Если для степенного ряда существует предел , то радиус сходимости , т.е. .

Для степенного ряда радиус сходимости находится также, но интервал сходимости симметричен относительно точки .

Пример

Найти область сходимости степенного ряда .

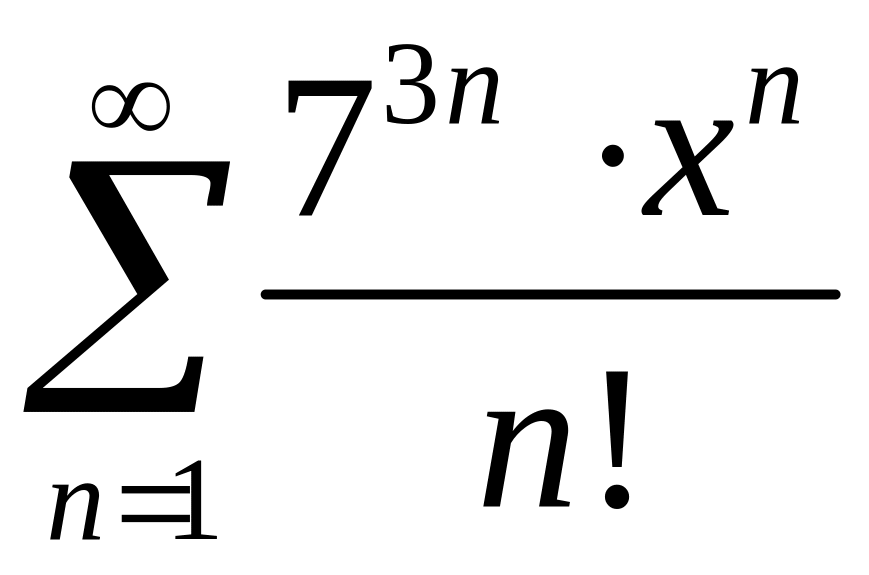Решение

Найдем радиус сходимости степенного ряда. Так как , , то

,

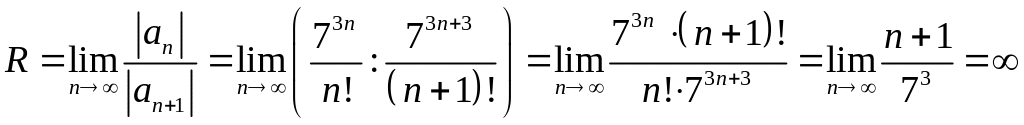следовательно, область сходимости данного степенного ряда .