1.5. Неустановившееся движение электропривода при постоянном динамическом моменте.

Неустановившееся движение возникает, когда не сохраняется равенство моментов: М М_с.

При этом динамический момент не будет равен нулю: М_дин=М-М_с 0, и происходит либо увеличение, либо уменьшение скорости ЭП.

Неустановившееся движение имеет место при пуске, торможении, реверсе двигателя, регулировании его скорости и при изменении нагрузки на валу двигателя. Таким образом, неустановившееся движение возникает при переходе ЭП из установившегося движения с одними параметрами к установившемуся движению с другими параметрами называется переходным процессом или переходным режимом ЭП.

Цель рассмотрения неустановившегося движения – это получение зависимостей следующих механических переменных ЭП.

1) Момента; 2) Скорости; 3) Угла поворота вала двигателя от времени

М=f(t)

ω=f(t)

=f(t)

Данные зависимости получаются при решении дифференциального уравнения движения ЭП:

М М_С=J* =

Для решения данных уравнений необходимо знать законы изменения моментов двигателя и нагрузки, массы и моменты инерции движущихся элементов и начальные условия.

В общем случае моменты двигателя и нагрузки могут являться функциями времени и координат движения.

Рассмотрим наиболее простой случай, когда момент нагрузки и момент двигателя являются постоянными М=const, М_C=const, а масса и момент инерции в переходных процессах не изменяются.

Для этого случая приведены следующие механические характеристики

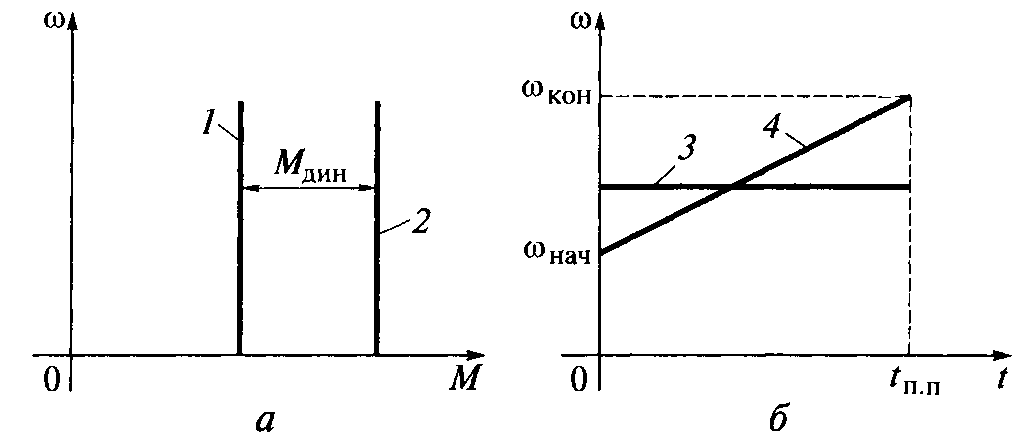
Механические характеристик а) и графики переходного процесса б) при постоянном динамическом моменте.

1) механическая характеристика ИО РМ;

2) механическая характеристика двигателя;

3) график момента;

4) график скорости.

Общий случай, показанный на графике, когда момент двигателя и момент нагрузки являются постоянными, а масса и момент инерции не изменяются во времени. Уравнение движения ЭП решается методом разделения переменных, после чего его решение примет вид:

=(M-M_C)*t/J+C

Постоянная интегрирования «С» находится из начальных условий t=0; ω=ω_нач; и будет равна:С= ω_нач

Таким образом, уравнение движения электропривода при данных условиях примет вид:

=((M-M_C))/J))+ _нач

В общем случае, когда время переходного процесса t 0, уравнение переходного процесса будет иметь вид:

t 0 => =((M-M_C))*t/J))+ _нач

Данное уравнение показывает, что при данных условиях скорость будет линейно зависеть от времени.

При этом, если разность моментов имеет знак «+» (М-М_с)>0, то скорость будет увеличиваться (график 4).

Если момент нагрузки больше чем момент двигателя, то скорость будет изменяться по характеристике 3, либо уменьшаться (М-М_с)<0.

Из уравнения решения движения ЭП можно определить время переходного процесса, за которое скорость будет изменяться от своего начального значения до конечного:

_{нач кон}

t_П.П=J*( _кон- _нач)/(М-М_С)

Угол поворота двигателя от времени переходного процесса определяется выражением:

=(М-М_С)*t²/(2*J)+ _нач*t+ _нач

Таким образом, угол поворота вала двигателя будет иметь квадратичную зависимость от времени переходного процесса.