1.1. Уравнение движения электропривода

В механическом движении участвуют подвижная часть электро­двигателя (ротор или якорь), элементы механической передачи, образующие механическую часть ЭП, а также исполнительный орган рабочей машины.

Движение любого элемента механической части ЭП или ис­полнительного органа рабочей машины подчиняется известным законам механики. Поступательное и вращательное движение опи­сывается следующими уравнениями:

где - соответственно совокупность сил и моментов, действующих на элемент; т и J - соответственно масса и момент инерции элемента; w и v - соответственно угловая и линейная скорости движения элемента; t – время.

Уравнения движения по своему характеру являются дифферен­циальными, поскольку содержат производные скорости, массы и момента инерции. Если масса и момент инерции элементов при движении не изменяются, то их производные в уравнениях (2.1) и (2.2) оказываются равными нулю и эти уравнения упрощаются:

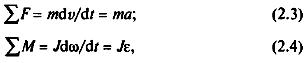
- соответственно ускорения при поступательном и вра­щательном движениях,

Уравнения (2.3) и (2.4) отражают известный закон механики: ускорение движения элемента (материального тела) пропорци­онально алгебраической сумме действующих на него сил (момен­тов) и обратно пропорционально его массе (моменту инерции).

Из этих уравнений следует условие движения с постоянной скоростью. Если

(2.5)

гоdv/dt = dw/dt = О и элемент движется с постоянной скоростъю или находится в состоянии покоя.

Другими словами, элемент будет двигаться с неизменной ско­ростью (или находиться в состоянии покоя), если сумма сил или моментов, к нему приложенных, будет равна нулю. Такое движе­ние называют установившимся. Условия (2.5) используются для определения параметров установившегося механического движе­ния.

При элемент будет двигаться с ускорени­ем, а при - с замедлением. Такие процессы носят название неустановившихся, или переходных. Зависимости изменения скорости элемента во времени (графики переходных процессов) v(t) или w(t) получаются путем решения (интегри­рования) уравнений (2.3) или (2.4) при известных действующих суммах сил или моментов, массе m или моменте инерции J, а также начальных значениях скорости.

Зависимости изменения во времени положения S или угла по­ворота ф элемента получаются с использованием следующих со­отношений:

1.2.Одномассовая система.

Одномассовая расчетная схема (жесткое приведен­ное механическое звено) получается после выполнения операции приведения, когда все механические элементы ЭП и исполни­тельный орган рабочих машин принимаются абсолютно жестки­ми, а зазоры в кинематической схеме не учитываются. Для наибо­лее распространенного случая, когда элементом приведения яв­ляется якорь или ротор двигателя вращательного движения, од­номассовая расчетная схема может быть представлена рис. 2.1, на котором М, М_с- соответственно момент двигателя и приведен­ный момент нагрузки; j - общий момент инерции, определяемый суммой момента инерции двигателя и приведенных к его валу мо­ментов инерции и масс элементов механической части ЭП и исполнительного органа рабочей машины, - угло­вая скорость вращения вала двигателя (в дальнейшем - скорость).

Рис. 2.1. Одномассовая расчетная схема механиче­ской части:

1 – двигатель

В общем случае моменты двигателя М и нагрузки М_С могут иметь как положительные, так и отрицательные знаки. Уравнение дви­жения (2.4) для одномассовой схемы может иметь вид:

Правило, по которому в формуле (2.11) определяются знаки моментов, следующее. Одно из направлений движения принима­ется положительным. Тогда моменты, направленные по движе­нию, имеют знак, совпадающий со знаком скорости, а моменты, направленные против движения - противоположный знаку ско­рости.

В основном для ЭП режиме работы двигатель создает движу­щий момент, а исполнительный орган рабочих машин - момент сопротивления движению. Тогда уравнение движения принимает следующий вид:

Левая часть этого уравнения, представляющая собой разность моментов двигателя и нагрузки и определяющая вместе с момен­том инерции J ускорение или замедление движения dw/dt, в те­ории ЭП получила название динамического момента

Мдин= М-Мс (2.13)

Таким образом, операция приведения позволяет перейти от реальных схем механической части ЭП и исполнительного органа рабочей машины к расчетной (эквивалентной) схеме, основой которой является двигатель (элемент приведения) со своей ско­ростью, а остальные элементы реальных схем представлены при­веденными моментом нагрузки (сопротивления) М_С и своими моментами инерции.