
- •Введение
- •1. Кинематический и силовой расчет привода
- •2 Расчет передач
- •2.1. Расчет клиноременной передачи
- •1. Выбор сечения ремня
- •2. Определение диаметров шкивов
- •3. Определение межосевого расстояния а и расчетной длины ремня l.
- •4. Определение угла обхвата ремнем ведущего шкива α1
- •5. Определение допускаемой мощности [p], передаваемой одним клиновым ремнем в условиях эксплуатации рассчитываемой передачи.
- •1. Выбор варианта термической обработки зубчатых колес
- •2. Предварительное определение допускаемого контактного напряжения при проектном расчете на сопротивление контактной усталости
- •3. Определение главного параметра конической передачи
- •4. Определение геометрических параметров, используемых при расчётах на прочность.
- •6. Предварительное определение внешнего диаметра вершин зубьев шестерни.
- •7. Проверка пригодности заготовок и выбор материала зубчатых колёс.
- •8. Выбор степени точности передачи.
- •9. Уточнение допускаемого контактного напряжения при проверочном расчёте на сопротивление контактной усталости.
- •10. Проверочный расчёт передачи на сопротивление контактной усталости.
- •11. Определение допускаемого напряжения изгиба при расчёте зубьев на сопротивление усталости при изгибе.
- •12. Проверочный расчёт зубьев на сопротивление усталости ори изгибе.
- •13. Проверочный расчёт передачи на контактную прочность при действии пиковой нагрузки (при кратковременной перегрузке).
- •14. Проверочный расчёт передачи при изгибе пиковой нагрузкой (при кратковременной перегрузке).
- •16. Выбор осевой формы зубьев конической передачи.
- •17. Геометрический расчёт конической передачи.
- •2.3 Расчет цепной передачи
- •1. Выбор типа приводной цепи.
- •2. Выбор чисел зубьев звёздочек.
- •3. Предварительное определение межосевого расстояния.
- •4. Определение коэффициента эксплуатации .
- •5. Определение коэффициентов и .
- •6. Выбор цепи.
- •7. Определение межосевого расстояния и длины цепи.
- •8. Силы в цепной передаче и требования монтажа.
- •3.Расчет и конструирование валов
- •3.1 Предварительный расчёт быстроходного (входного) вала.
- •3.2 Приближенный расчет быстроходного вала.
- •3.3 Проверочный расчет быстроходного вала
- •3.4 Предварительный расчет тихоходного (выходного) вала.
- •3.5 Приближенный расчет тихоходного вала
- •3.6 Проверочный расчет тихоходного вала
- •4. РАсчет шпоночных соединений
- •4.1 Шпоночное соединение быстроходного вала.
- •4.2 Шпоночное соединение тихоходного вала.
- •5. Расчет и конструирование подшипниковых узлов
- •5.1 Проверочный расчет подшипников быстроходного вала
- •5.2 Проверочный расчет подшипников тихоходного вала
- •6. Коструирование шкивов, зубчатых колес и звездочек
- •6.1 Определение размеров шкивов:
- •6.2 Определение размеров конической шестерни и конического колеса:
- •6.3 Определение размеров звездочек:
- •7. Конструирование корпусных деталей и крышек
- •8. Смазывание зацеплений
- •9. Выбор и проверочный расчет муфт
- •10. Конструирование рамы (плиты)
- •11. Выбор посадок
- •12. Сборка и регулировка редуктора
- •13. Техника безопасности
- •Заключение
- •Список использованной литературы
13. Проверочный расчёт передачи на контактную прочность при действии пиковой нагрузки (при кратковременной перегрузке).
Цель
данного расчета – проверка статической
прочности зубьев при кратковременных
перегрузках, не учтенных при расчете
на сопротивление контактной усталости.
Предельно допускаемое контактное
напряжение
 ,
не вызывающее остаточных деформаций
или хрупкого разрушения поверхностного
слоя обычно определяют для менее прочного
зубчатого колеса. В нашем примере менее
прочным является колесо, для которого
по табл. 1П.9 приложения 1П [1, c.371]
(материал колеса – сталь 40Х,
,
не вызывающее остаточных деформаций
или хрупкого разрушения поверхностного
слоя обычно определяют для менее прочного
зубчатого колеса. В нашем примере менее
прочным является колесо, для которого
по табл. 1П.9 приложения 1П [1, c.371]
(материал колеса – сталь 40Х,
 ,
где
,
где
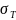 – см. табл. 1П.7 приложения 1П
[1, c.370].
– см. табл. 1П.7 приложения 1П
[1, c.370].
Тогда условие контактной прочности при действии пиковой нагрузки:
 (2.67)
(2.67)
где
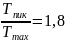 – кратковременная перегрузка привода
(см. исходные данные);
– кратковременная перегрузка привода
(см. исходные данные);
 – см. п. 10.
– см. п. 10.
 .
.
Условие контактной прочности выполняется.
14. Проверочный расчёт передачи при изгибе пиковой нагрузкой (при кратковременной перегрузке).
Цель данного расчета – проверка статической прочности зубьев при кратковременных перегрузках, не учтенных при расчете зубьев на сопротивление усталости при изгибе. При этом расчет проводят отдельно для шестерни и колеса.
Предельно допускаемое напряжение изгиба, не вызывающее остаточных деформаций или хрупкого излома зуба, для принятого варианта термообработки по табл. 1П.9 приложения 1П [1, c.371]:
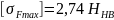 (2.68)
(2.68)
;
..
Тогда условие прочности передачи при изгибе пиковой нагрузкой:
 (2.69)
(2.69)
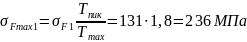 ;
;
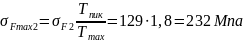 ,
,
где
 и
и
 – см. п. 12.
– см. п. 12.
Таким образом, прочность зубьев при изгибе пиковой нагрузкой обеспечивается.
15.
Определение сил в зацеплении конической
передачи.
Равнодействующую сил нормального
давления
 обычно считают приложенной в среднем
сечении зуба на диаметре
обычно считают приложенной в среднем
сечении зуба на диаметре
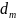 и раскладывают на три составляющие:
окружную силу
и раскладывают на три составляющие:
окружную силу
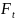 радиальную силу
радиальную силу
 и осевую силу
и осевую силу
 .
.
Однако, прежде чем определить силы , и , установим направление вращения шестерни конической передачи. Это направление будет зависеть от того, в каком направлении должен вращаться приводной вал. Обычно приводные валы цепных и ленточных конвейеров нереверсивны, т.е. вращаются только в одном направлении. При этом направление вращения приводного вала выбирается таким образом, чтобы грузовая ведущая ветвь тягового элемента (цепи или ленты) набегала на приводную тяговую звездочку (у цепного конвейера) или барабан (у ленточного конвейера). Грузовой чаще всего является верхняя ветвь тягового элемента. В нашем примере редуктор устанавливается в приводе цепного конвейера, где направление вращения приводного вала указано на схеме привода. Для того, чтобы обеспечить указанное направление (против часовой стрелки) необходимо, чтобы шестерня конической передачи вращалась по часовой стрелке, если смотреть на нее с вершины делительного конуса.
Определим теперь величины сил , и .
В
отличие от передачи с прямыми зубьями,
в которой осевая сила на шестерне
 всегда направлена от вершины делительного
конуса к основанию, в передаче с круговыми
зубьями такое наблюдается не всегда. В
последней может быть случай, когда сила
направлена от основания к вершине
конуса.
всегда направлена от вершины делительного
конуса к основанию, в передаче с круговыми
зубьями такое наблюдается не всегда. В
последней может быть случай, когда сила
направлена от основания к вершине
конуса.
Осевая
сила на шестерне
 ,
будет положительна, т.е. направлена от
вершины конуса к основанию в том случае,
если направление линии зуба шестерни
совпадает с направлением её вращения
(если смотреть на шестерню с вершины
конуса). Например, направление линии
зуба шестерни правое, направление её
вращения - по часовой стрелке или
направление линии зуба шестерни левое,
направление её вращения - против часовой
стрелки (см. рис. 4,а, б в табл. 1П.23 приложения
1П
[1, c.383]).
,
будет положительна, т.е. направлена от
вершины конуса к основанию в том случае,
если направление линии зуба шестерни
совпадает с направлением её вращения
(если смотреть на шестерню с вершины
конуса). Например, направление линии
зуба шестерни правое, направление её
вращения - по часовой стрелке или
направление линии зуба шестерни левое,
направление её вращения - против часовой
стрелки (см. рис. 4,а, б в табл. 1П.23 приложения
1П
[1, c.383]).
Осевая сила на шестерне направлена от основания к вершине конуса в том случае, если направление линии зуба шестерни не совпадает с направлением её вращения (см. рис. 5, а, б табл. 1П.23 приложения 1П [1, c.383]). Следует отметить, что последний случай может наблюдаться в реверсивных передачах.
Рекомендации по определению сил в зацеплении конической передачи с круговыми зубьями приведены в табл. 1П.23 приложения 1П [1, c.382].
В
нашем примере мы установили, что шестерня
должна вращаться по часовой стрелке.
Следовательно, для того, чтобы осевая
сила на шестерни
была направлена от вершины конуса к
основанию, принимаем направление линии
зуба шестерни - правое, колеса - левое.
Тогда
окружная сила на шестерне и колесе
 ,
где
,
где
 – см. п. 10.
– см. п. 10.
Для
нахождения радиальной
 и осевой сил
на шестерне определим предварительно
коэффициенты радиальной
и осевой сил
на шестерне определим предварительно
коэффициенты радиальной
 осевой
осевой
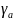 ,
сил для случая, когда направление линии
зуба шестерни совпадает с направлением
её вращения:
,
сил для случая, когда направление линии
зуба шестерни совпадает с направлением
её вращения:
 (2.70)
(2.70)
 ;
;
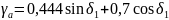 (2.71)
(2.71)
 .
.
Тогда:
радиальная сила на шестерне
 (2.72)
(2.72)
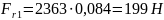 ;
;
осевая сила на шестерне
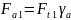 (2.73)
(2.73)
 ;
;
осевая
сила на колесе
 ;
;
радиальная
сила на колесе
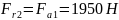 .
.
Схема сил для данного случая приведена на рис. 7,а (см. табл. 1П.23 приложения 1П [1, c.384]).
