4.Линии уровня

Определение линии уровня. Пусть некоторое число, тогда линия уровня функции f(x), соответствующая числу :

Линии уровня линейной функции представляют из себя параллельные прямые; линии уровня квадратичной фунции линии второго порядка: эллипсы, гиперболы, параболы, а также параллельные прямые, точка, ;. Через каждую точку плоскости проходит какаято линия уровня; линии уровня не пересекаются. Линии уровня ортогональны градиенту функции в точке.

4.1.Построение линий уровня для функции первого порядка

7

Рис. 1: График с линиями уровня при = 0; 1; 2

4.2.Построение линии уровня для функции второго порядка

Пусть задана функция:

Необходимо найти линию уровня для = 3. Приведение заданной функции к другому виду:

1. Чтобы упростить решение, необходимо переставить некоторые элементы:

[2x22 6x1x2 + x21] + 6x1 3 = 0

2. Многочлен в квадратных скобках, очевидно квадрат разности, нужно его собрать:

p 2

2 x22 2 3x1x2 + 1x21 =

3. После преобразования первого многочлена выражение принимает следующий вид:

8

4. Многочлен в квадратных скобках, очевидно квадрат разности с изменёнными знаками

Выражение (7) эквивалентно (6), так как было получено путём эквивалентных преобразований. Теперь оно имеет канонический вид линии второго порядка, а именно гиперболы, поэтому необходимо построить новую систему координат x0Oy0 на основе старой, для этого нужно найти ось абсцисс и ось ординат.

1.Для получения оси абсцисс Ox0 необходимо приравнять второй квадрат к нулю и к единице:

s s

ss

ss

9

2.Для получения оси ординат Oy0 необходимо приравнять первый квадрат к нулю и к единице:

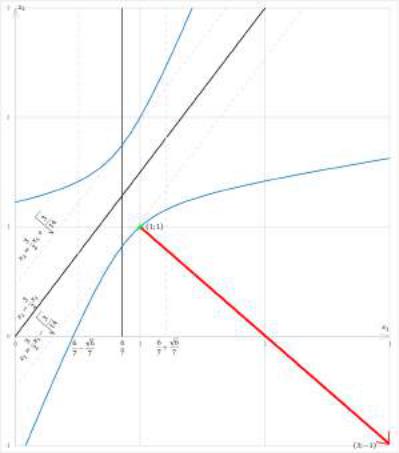
3.Расчётами выше были определены новые координатные оси, теперь лишь осталось построить гиперболу.

Вычисление градиента в точке (1; 1) fx01 = 2x1 6x2 + 6

fx02 = 6x1 + 4x2 fx01 (1; 1) = 2

fx02 (1; 1) = 2

2 rf = 4

Рис. 2: График линии уровня и градиента функции двух переменных

10