Содержание
1. Определение порядков малости |
3 |
1.1.Правая формула численного дифференцирования . . . . . . . . . . . . . . . . . . 3
1.2.Центральная формула численного дифференцирования . . . . . . . . . . . . . . 4
1.3.Формулы численного интегрирования методом прямоугольников . . . . . . . . . 5
1.4.Формулы численного интегрирования методом трапеций . . . . . . . . . . . . . . 6
2.Программный способ нахождения порядков малости бесконечно малых ве-
личин |
8 |
2.1.Численный анализ бесконечно малых величин . . . . . . . . . . . . . . . . . . . . 8
2.2.Численный анализ бесконечно большой величины . . . . . . . . . . . . . . . . . . 9
3. Дробные производные |
10 |
3.1. Вычисление дробных производных |
. . . . . . . . . . . . . . . . . . . . . . . . . . 10 |
3.2.Вычисление дробных производных для дробной степени . . . . . . . . . . . . . . 10
3.3.Разложение степенного ряда . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4. |
Анализ бесконечно малых функций нескольких переменных |
12 |
|
|
4.1. |
Вычисления для ортогонального вектора . . . . . . . . . . . . . . . . . . . . . . . |
13 |
|
4.2. |
Вычисление графика порядков малости . . . . . . . . . . . . . . . . . . . . . . . |
14 |
A Программный анализ бесконечно малых |
15 |
||
B |
Тест анализатора бесконечно малых |
19 |
|
C |
Программный анализ алгоритма пузырьковой сортировки |
22 |
|
D |
Тест анализатора пузырьковой сортировки |
25 |
|
E |
Программный анализ БМФ многих переменных |
26 |
|
F |
Тест анализатора БМФ многих переменных |
34 |
|
1. Определение порядков малости
Дана функция |
|
sin(6x) + px2 + 6x |
(1) |
Определение порядка малости и константы C погрешности '(h).
1.1.Правая формула численного дифференцирования
0 |
(x) |
f(x + h) f(h) |
(2) |
||||
f |
|
|
h |
|
|||
Для начала вычислим производную аналитически |
|
||||||
6 cos(6x) + |
p |
x + 3 |
(3) |
||||
|
|
||||||
x2 + 6x |
|
|
|||||
При x = 6: f0(6) 0:292878, если значение в косинусе указано в радианах.
1.В Excel вычисляем значения по формуле 2, постепенно уменьшая порядки малости h до 20, чтобы заметить эффект неточных вычислений после lg(h) = 8 и эффект невозможных вычислений после lg(h) = 14, которые вызваны неточными машинными вычислениями (в Excel m = 10 16);
2.для каждого значения находим погрешность '(h) = f0(x) f~0(x), где f~0(x) формула численного дифференцирования;
3.логарифмируем порядки малости и найденные погрешности;
4.строим график lg(h)-lg('(h)) см. рис. 1.
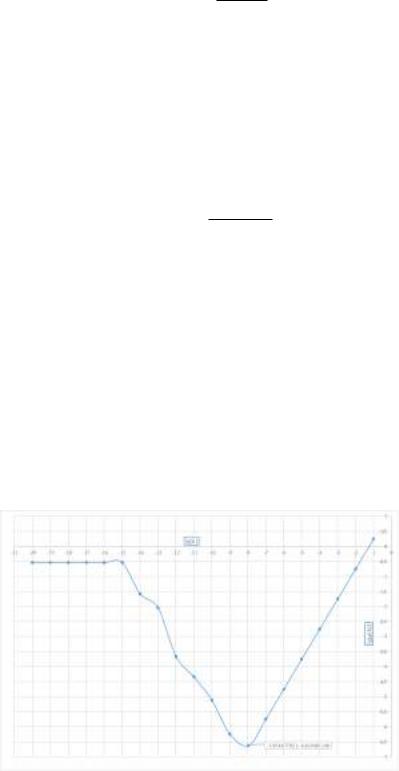
Рис. 1: lg-lg график погрешности правой формулы численного дифференцирования
3
На графике видно, что в начале вычислений график явно представляет собой линейную функцию вида x + k, после lg(h) = 8 график представляет собой непонятную функцию, стремящуюся к оси O ln(h), а после lg(h) = 15 график представляет собой линию lg('(h)) = lg(f0(h)) 0:29, так как численно производная в этом промежутке и далее равна 0.
Для определения порядка малости вычислим линию тренда в промежутке [-8; -1]; по итогу средний коэффициент 0:99. Для определения k нужно найти точку пересечения линейной функции с осью O ln('), она оказывается: k 1:23, тогда C = 10k 16:9824.
1.2.Центральная формула численного дифференцирования
f(x + h) f(x h)
f0(x) (4)
2 h
Аналитически производная функции 1 представлена в 3.
При x = 6: f0(6) 0:292878, если значение в косинусе указано в радианах.
1.В Excel вычисляем значения по формуле 4, постепенно уменьшая порядок малости h до 20, чтобы заметить эффект неточных вычислений после lg(h) = 5 и эффект невозможных вычислений после lg(h) = 14, которые вызваны неточными машинными вычислениями (в Excel m = 10 16);
2.для каждого значения находим погрешность '(h) = f0(x) f~0(x), где f~0(x) формула численного дифференцирования;
3.логарифмируем порядок малости и найденные погрешности;
4.строим график lg(h)-lg('(h)) см. рис. 2.
Рис. 2: lg-lg график погрешности центральной формулы численного дифференцирования
4
На графике видно, что в начале вычислений график явно представляет собой линейную функцию вида x + k, после lg(h) = 5 график представляет собой непонятную функцию, стремящуюся к оси O ln(h), а после lg(h) = 15 график представляет собой линию lg('(h)) = lg(f0(h)) 0:29, так как численно производная в этом промежутке и далее равна 0.
Для определения порядка малости вычислим линию тренда в промежутке [-5; -1]; по итогу средний коэффициент 2:01. Для определения k нужно найти точку пересечения линейной функции с осью O ln('), она оказывается: k 0:69, тогда C = 10k 4:8978.
1.3.Формулы численного интегрирования методом прямоугольников
!
Z ai+1 f(x)dx (ai+1 ai) f ai + ai+1 (5)
ai 2
Для начала вычислим интеграл функции аналитически
( |
|
+ 3) |
|
|
|
9 |
2 |
|
|
|
|
6 |
(6) |
|
x |
px2 |
+ 6 |
(x + 3) + px2 + 6x |
|||||||||||
|
|
x |
|
ln |
|
|
cos(6x) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для пределов интегрирования a = 6, b = 12 значение интеграла: R612 69:7996.
Прим.: для численного интегрирования методом прямоугольников нужно разделить общую площадь на N частей, поэтому сложность алгоритма O (10x), что означает, при некоторой итерации время выполнения резко возрастёт, поэтому вычисления произведены только до 108 итераций. В качестве числа h выступит значение 6=10i.
1.В Excel вычисляем значения по формуле 5, постепенно увеличивая N, тем самым уменьшая h до 6 10 9;
2. для каждого значения находим погрешность ~ , где первооб-
'(h) = F (x) F (x) F (x)
разная для , ~ первообразная, вычисленная по численной формуле; f(x) F (x)
3.логарифмируем порядок малости и найденные погрешности;
4.строим график lg(h) lg('(h)) см. рис. 3.
5
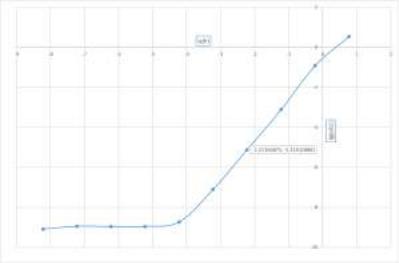
Рис. 3: lg-lg график погрешности численного интегрировния методом прямоугольников
На графике видно, что в начале вычислений график явно представляет собой линейную функцию вида x + k, после lg(h) = 5 график представляет собой другую функцию.
Для определения порядка малости вычислим линию тренда в промежутке [-5; -1]; по итогу средний коэффициент 1:91. Для определения k нужно найти точку пересечения линейной функции с осью O ln('), она оказывается: k 0:7861, тогда C = 10k 0:1636.
1.4.Формулы численного интегрирования методом трапеций
Zaiai+1 f(x)dx (ai+1 ai) |
f(ai) + f(ai+1) |
(7) |
2 |
Аналитически интеграл функции 1 представлен в 6. Для пределов интегрирования a = 6, b = 12 значение интеграла: R612 69:7996.
Прим.: для численного интегрирования методом прямоугольников нужно разделить общую площадь на N частей, поэтому сложность алгоритма O (10x), что означает, при некоторой итерации время выполнения резко возрастёт, поэтому вычисления произведены только до 108 итераций. В качестве числа h выступит значение 6=10i.
1.В Excel вычисляем значения по формуле 7, постепенно увеличивая N, тем самым уменьшая h до 6 10 9;
2. для каждого значения находим погрешность ~ , где первооб-
'(h) = F (x) F (x) F (x)
разная для , ~ первообразная, вычисленная по численной формуле; f(x) F (x)
3.логарифмируем порядок малости и найденные погрешности;
4.строим график lg(h) lg('(h)) см. рис. 4.
6
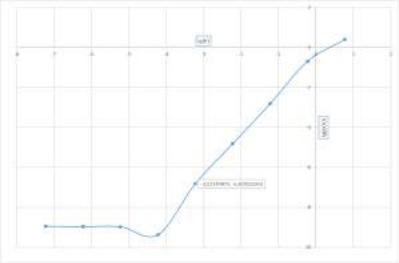
Рис. 4: lg-lg график погрешности численного интегрировния методом трапеций
На графике видно, что в начале вычислений график явно представляет собой линейную функцию вида x + k, после lg(h) = 4 график представляет собой другую функцию.
Для определения порядка малости вычислим линию тренда на отрезке [-4; -1]; по итогу средний коэффициент 2:13. Для определения k нужно найти точку пересечения линейной функции с осью O ln('), она оказывается: k 0:1628, тогда C = 10k 0:6873.
7