14. Важнейшие группировки и классификации, применяемые в статистике.

Признаки, по которым проводится группировка, называют группировочными признаками. Группировочный признак иногда называют основанием группировки. Правильный выбор существенного группировочного признака дает возможность сделать научно обоснованные выводы по результатам статистического исследования. Группировочные признаки могут иметь как количественное выражение, так и качественное.

При определении числа групп, как правило, учитываются задача исследования, объем совокупности и виды признаков, которые берутся в качестве основания группировки.

В основе любой группировки лежит классификационный или группировочный признак. Это показатель, по которому происходит разделение совокупности данных на группы. Каждая единица в совокупности данных обладает общим признаком, и в зависимости от его значения относится к той или иной группе.

Все виды группировок можно разделить на два типа в зависимости от характера группировочного признака. Первый тип – это логическая группировка, когда в качестве классификационного показателя выступает логический признак. Второй тип – статистическая группировка, когда в качестве классификатора используется статистический показатель. Примером первого типагруппировки (логической) может служить разделение товаров по поставщикам или предприятий по регионам. То есть по признакам, которые существуют сами по себе и не требуют проведения каких-либо расчетов. Второй вид группировок (статистический) – разделение товаров по объемам продаж или стоимости складских запасов. Такая группировка подразумевает расчет некоторого статистического показателя для каждой единицы анализируемой совокупности и, в зависимости от его значения, разбиение данных на группы по заданным границам.

Зачастую группировка данных осуществляется сразу по нескольким признакам, в том числе по разным типам (логическим и статистическим). В результате получается многомерная группировка, когда каждому элементу анализируемой совокупности соответствует несколько характеристик, а их сочетание определяет группу, в которую попадает данный элемент.

15. Ряды распределения, их виды и графическое изображение.

Ряды распределения–группировка по одному признаку. Они пр.с. группировку, где известна численность единиц в группах или удельный вес группы в общем итоге. По форме это простейшая разновидность структурной группировки по одному признаку в групповой таблице с двумя графами: группы по выделенному признаку и численности групп. Численные значения признака в рядах распределения называютсявариантами, а численность каждой группы – частотами (f). Сумма всех частот определяет численность всей совокупности, или ее объем (n).

Ряды распределения подразделяются на атрибутивные (группировка по атрибутивным признакам) ивариационные (по количественным признакам). По характеру вариации признака различают вариационные ряды распределения прерывные (дискретные) и непрерывные (интервальные). В первом случае признак изменяется прерывно, т.е. через определенное число единиц. Во втором группировочный признак в определенном интервале может принимать любые значения.

Анализ рядов распределения сопровождается их графическим изображением. Для отображения вариационных рядов распределения используются следующие графики: полигон, гистограмму и кумуляту. 

Полигон применяют для графического изображения дискретного вариационного ряда, и этот график является разновидностью статистических ломаных.

Гистограмма применяется для графического изображения непрерывных (интервальных) вариационных рядов. Его построение аналогично построению столбиковых диаграмм. Гистограмма может быть преобразована в полигон распределения.

Кумулята изображает кумулятивные ряды распределения.

Величина равного интервала опр-ся по формуле:

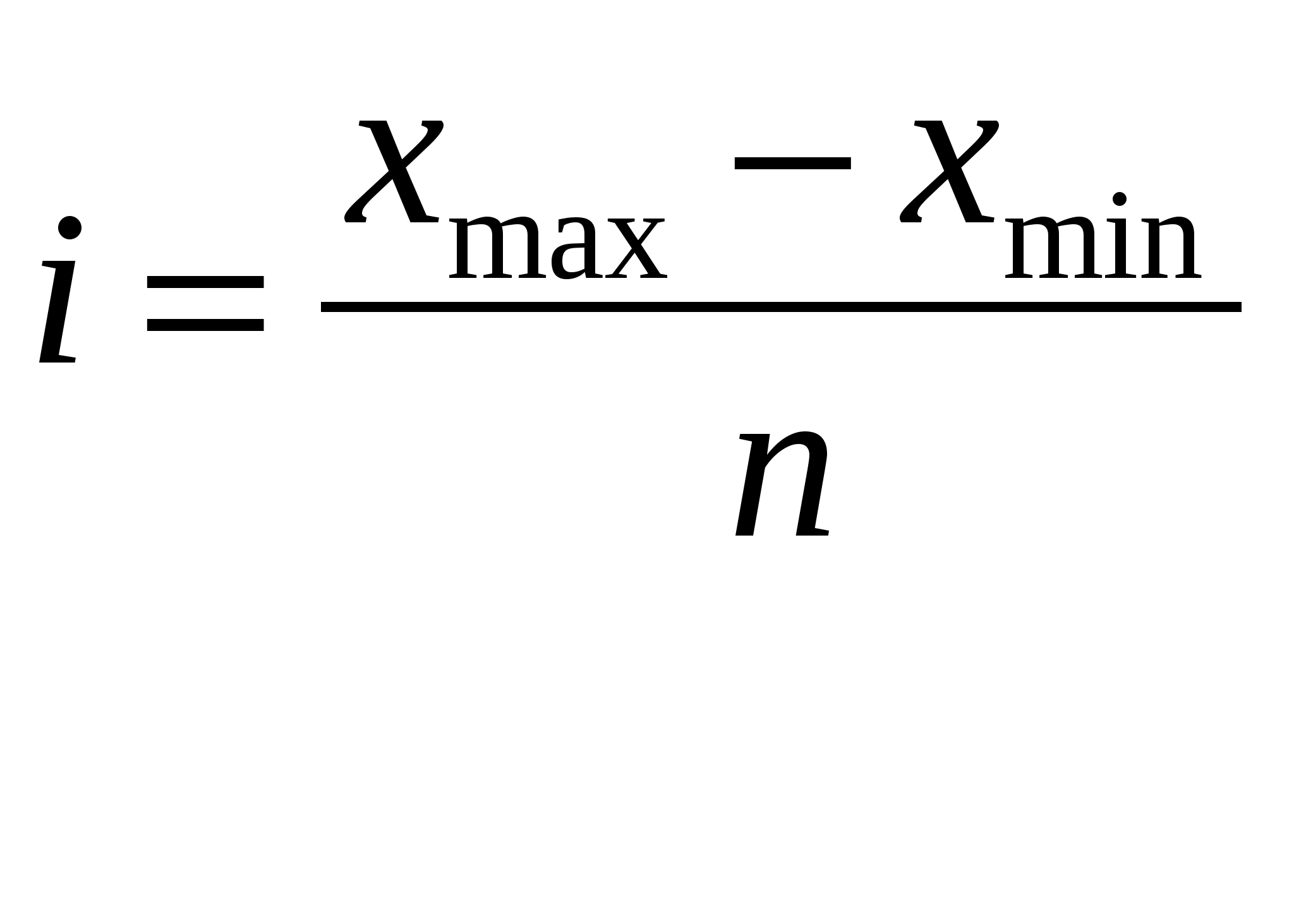, где X_max – максимальная среднегодовая стоимость основных производственных фондов; X_min – минимальная среднегодовая стоимость основных производственных фондов; n – количество групп.