26. Мода и медиана, их смысл и значение в социально-экономических исследованиях, способы вычисления.
Мода (М0) – величина признака (варианта), которая встречается в ряду распределения с наибольшей частотой (весом). В дискретных рядах распределения значение моды определяется визуально, т.е. по наибольшей частоте. Если же варианты ряда распределения заданы в виде интервалов, равными по величине, то сначала находится модальный интервал, т.е. интервал, обладающий наибольшей частотой, а затем – приближенное значение модальной величине признака по формуле
Мо
=Х𝑚𝑜+𝑖𝑚𝑜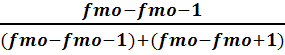
Где
– нижняя граница модального интервала;
– величина модального интервала;
𝑓𝑚𝑜−1
–
частота интервала, предшествующего
модальному; 
– частота модального интервала; 
– частота интервала, следующего за
модальным.
Медиана (Ме) – величина признака у единицы совокупности, находящейся в середине ранжированного (упорядоченного) ряда. Если ряд распределения представлен конкретными индивидуальными значениями признака в ранжированном порядке, то величина медианы находится как серединное значение признака той единицы, которая делит совокупность на 2 равные части.
Если варианты в ряду распределения представлены в виде равных интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для определения этого интервала сумму частот (∑f) делят пополам, и на основе последовательного накопления (суммирования)частот интервалов, начиная с первого, находят интервал, где расположена медианная единица. Приближенное значение медианы в медианном интервале исчисляется по формуле
Ме
= 𝑥𝑚𝑒+𝑖𝑚𝑒
Где
– нижняя граница медианного интервала;
– величина медианного интервала; ∑f
– сумма частот ряда; 𝑆𝑚𝑒−1
–
накопленный итог численностей до
медианного интервала; 
– частота медианного интервала.
27. Статистическое изучение вариации. Показатели вариации и методы из расчета.
Вариация – это изменение (колеблемость) значений признака в пределах изучаемой совокупности при переходе от одного объекта к группе объектов, от одного случая к другому. Изучение вариации в статистической практике позволяет установить зависимость между изменением, которое происходит в исследуемом признаке, и теми факторами, которые вызывают данное изменение.
Для измерения вариации признака используют как абсолютные, так и относительные показатели, которые позволяют: определить степень связи между признаками; оценить степень однородности совокупности; типичности и устойчивости средней; определить величину погрешности выборочного наблюдения; статистически оценить закон распределения совокупности.
Абсолютные показатели:
Размах вариации (R)пр.с. разность между максим. (Хmax) и минимальным (Хmin) значениями признака в совокупности (в ряду распрделения):
R = Хmax – Хmin.
Разность между отдельным значением признака и средней называют отклонением.
Среднее линейное отклонение (l) вычисляется по формулам: по индивид-ным (несгруппированным) данным
= 
По вариационным рядам (сгруппированным данным):
= 
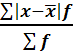
Дисперсия и среднее квадратическое отклонение. Среднее линейное отклонение относительно редко применяется для оценки вариации признака. Поэтому обычно вычисляются дисперсия (
)
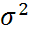и среднее квадратическое отклонение
(
).
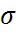Эти показатели применяются не только
для оценки вариации признака, но и для
изменения связи между ними, оценки
величины ошибки выборочного наблюдения
и других целей.
Относительные показателирассчит-ся как отношение ряда абсол.пок-лей вариации к их средней арифметической:
Коэффициент осцилляции:
𝐾𝑅=
100
Относительное линейное отклонение:
𝐾
=
100
Коэффициент вариации:
