25. Вынужденные колебания. Резонанс.

Вынужденные колебания – колебания, которые происходят под действием внешней периодически изменяющейся силы.

Дифференциальное уравнение вынужденных колебаний

В правой части стоит выражение для внешней вынужденной периодически изменяющейся силы. Полученное уравнение представляет собой неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Неоднородное, т.к. правая часть не равна 0.

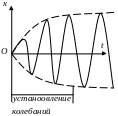
Решение данного уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного уравнения . Выражение для x₁ играет сущ. роль только в начальной стадии процесса (при установлении колебаний до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, опред. выражением. .

Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы

Величина смещения x вынужденных колебаний в присутствии вынужденной силы зависит от частоты, с которой изменяется данная сила. Это приводит к тому, что амплитуда вынужденных колебаний также зависит от частоты . Из последней формулы видно, что А максимальна, если знаменатель минимален.

Отриц. корень не подходит, т.к только положит значение имеет физ. смысл. Корень ₁=0 означает отсутствие внешней периодич. силы, тогда - решение ур-я, удовл. физич. требов.

Если =0 или близок к 0, то _рез=₀-собственная.

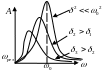
При ²<<₀²

26. Сложение колебаний одного направления и одинаковой частоты. Биения.

Пусть тело одновременно участвует в 2-х гармонических колебаниях, происходящих вдоль оси x

Результирующую силу определяем с помощью диаграммы. В векторном представлении колебания представляются в виде вектора, длина которого пропорциональна амплитуде, а направление вектора образует с осью X, который равен начальной фазе

Тогда результирующая амплитуда определяется по формуле:

Начальная фаза результирующего колебания определяется по тангенсу.

Уравнение результирующего колебания

Анализ выражения показывает, если , где k=0,1,2…, то результирующая амплитуда . Если , то A не изменяется со временем

Биения.

Если происходит сложение колебаний различной частоты, то вектора и имеют различные скорости вращения, следовательно результирующий вектор A изменяется по величине с течением времени и его скорость вращения не постоянна. Т.о. в этом случае наблюдается не гармонический, а более сложный колебательный процесс.

Периодические изменения амплитуды колебания, возникающие при сложении 2-х гармонических колебаний с близкими частотами ( ) называются биениями

Пусть частота одного колебания , а другого . Начальные фазы колебаний равны нулю, а , тогда

Складывая эти выражения, и учитывая, что , получим

В этом выражении величина ввиду ее малости не учтена. Т.к. , то время, за которое множитель совершит несколько полных колебаний, множитель практически не изменится. Это позволяет рассмотреть результирующее колебание как гармоническое с частотой , амплитуда которого изменяется по закону

Частота биения , тогда