Билет 1

2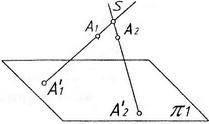 метода проекций:

Центральное проецирование

S – центр проекций

A’₁ , A’’₂ - центральные проекции

Центральной проекцией точки называется точка пересечения с плоскостью проекции проецирующего луча, проходящего через центр проекции и данную точку.

п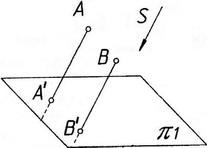араллельное проецирование

S – направление

Параллельной проекцией точки называется точка пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.

Центральной проекцией очки называется точка пересечения с плоскостью проекций проецирующего луча, проходящего через центр проецирования и данную точку.

Параллельной проекцией точки называется точка пересечения с плоскостью проекций проходящего через данную точку проецирующего луча, параллельного направлению проецирования.

Основные инвариантные свойства параллельного проецирования:

1)проекция точки на плоскость есть точка.

2)проекция прямой на плоскость в общем случае есть прямая. Она вырождается в точку, если прямая параллельна направлению проецирования.

3)если точка принадлежит линии, то проекция точки принадлежит проекции этой линии.

4)если отрезок прямой линии делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении.

5)точка пересечения линий проецируется в точку пересечения их проекций.

6)проекции отрезков параллельных прямых параллельны, и их длины находятся в таком же отношении, как и длины проецируемых отрезков.

7)проекции двух скрещивающихся прямых линий в зависимости от направления проецирования могут пересекаться или быть параллельными.

8)при прямоугольном проецировании прямой угол проецируется без искажения(прямым углом), если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна ей.

9)плоская фигура, параллельная плоскости проекций проецируется на эту плоскость без искажения.

10)при параллельном перемещении фигуры или плоскости проекций изображение фигуры на этой плоскости не изменяется.

Билет 2

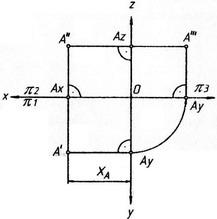
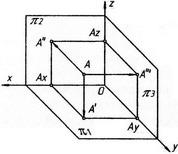
Проекции точки на три плоскости проекций

При проецировании определяю 3 вида проекции: горизонтальная фронтальная и профильная. При горизонтальном проецировании, точка проецируется на плоскость П1 и имеет название А’, при фронтальном проецирование точка имеет название А’’, а при профильном А’’’. все проекции точек переносятся по линиям связи

Координата точки - число, абсолютная величина которого, равна расстоянию от точки до соответствующей плоскости проекции.

Независимо от расположения точек в пространстве на комплексном чертеже их горизонтальные и фронтальные проекции соединяются линией связи, перпендикулярной оси Х.

Если известны горизонтальные и фронтальные проекции точек, то для определения ее профильной проекции следует из фронтальной проекции точки провести прямую перпендикулярную оси Z, на этой прямой от точки ее пересечения с осью Z отложить отрезок равный по величине координате Y. Откладываем вправо если Y положительна и влево, если Y отрицательна

Билет 3

Построение проекции отрезка:

Соединить прямыми одноименные проекции точек (концов отрезка) получим проекцию отрезка прямой.

Проекция прямой общего положения: прямая.

Прямые уровня. Для фронтали Y = const, для горизонтали - Z = const, для профильной прямой - X = const.

Проецирующие прямые. Горизонтальная проекция горизонтально проецирующей прямой вырождается в точку. На п2 и п3 проецируется без искажения. Фронтально проецирующая - на п1 и п3. Профильно проецирующая - на п1 и п2.

Деление отрезка. Из инвариантных свойств известно что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же отношении. Для графического деления отрезка прямой используют теорему Фалеса(параллельные прямые, пересекающие стороны угла, отсекают от стороны угла пропорциональные отрезки).

Натуральная величина отрезка. Необходимо построить гипотенузу прямоугольного треугольника, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, другим катетом - отрезок, равный по величине алгебраической разности координат Z (Y) крайних точек отрезка.

Натуральную величину угла находят из прямоугольного треугольника, который строят для определения натуральной величины отрезка прямой.