21. Колебания. Положение равновесия. Гармонические колебания.

Колебания – процессы, которые повторяются с течением времени.

Колебания системы вне зависимости от ее называют осциллятором. Тело или точка находится в положении равновесия, если сумма сил и сумма моментов сил, действующих на тело = 0. Различают равновесие устойчивое, неустойчивое, безразличное. Устойчивое – если при выведении тела из положения равновесия возникает сила, стремящаяся вернуть тело обратно. Неустойчивое – если при выведении тела из положения равновесия возникает сила, стремящаяся увести тело еще дальше от положения равновесия. Безразличное равновесие не характеризуется возникновением каких-либо определенных сил (тело не стремится ни вернуться, ни продолжить движение). В зависимости от характера взаимод. колебл. силы различ. свободные (собственные) колебания, вынужденные, затухающие, автоколебания.

Свободные колебания – колебания, которые соверш. за счет первоначально сообщ. энергии при последующем отсутствии внешних взаимодействий на колеб. сист.

Гармонические колебания – колебания, при которых колеблющ. величина измен. со временем по закону косинуса или синуса. .

Амплитуда – максимальное по модулю отклонение колеблющ. величины от его среднего значения.

Аргумент косинуса называется фазой колебаний. Начальная фаза ₀ определяет смещение в t=0.

Период колебаний – время одного полного колебания.

Частота колебаний – число полных колебаний в ед. времени.

Скорость – первая производная от смещения.

Ускорение – вторая производная от смещения.

Знак «-» означает, что ускорение колеблющ. точки направлено в сторону против смещения, т.е. ускорение и смещение изменяются в противофазе.

Скорость достигает максимального значения когда , т.е когда проходит среднее значение смещения. В этот момент смещение и ускорение = 0.

22. Пружинный маятник. Энергия пружинного маятника.

Пружинный маятник – это тело, прикрепленное к концу упругой пружины, другой конец которой закреплен и совершает колебания под действием силы упругости

Е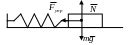 сли пружина растянута, на брусок действует сила упругости со стороны пружины. Эта сила всегда направлена так, чтобы вернуть брусок в положение равновесия. Пусть тело массой m закреплено на пружине, упругость которой k. В отсутствии сил трения на тело, выведенное из состояния равновесия, действует сила упругости . На основе 2-го закона:

Введем

Данное выражение является дифференциальным уравнением, описывающим движения пружинного маятника. Величина называется циклической частотой колебания.

Будем искать решения уравнения в виде функции , тогда

x₁ и x₂ являются частными решениями уравнения гармонических колебаний.

. Постоянные С₁ и С₂ можно найти, предположив, что в начальный момент времени известны скорость и смещение. Используя формулу Эйлера:

Получаем общее решение дифференциального уравнения.

, где А и ₀ - амплитуда и начальная фаза, для определения которых надо знать нач. условия.

Каждое конкретное колебание характеризуется определенным значением A и . Тело данной массы m, находясь под действием одной и той же упругой силы может совершать колебания с различной амплитудой и , но период колебаний всегда остается одним и тем же

Энергия маятника в произвольный момент времени равна сумме его энергий: и упругой деформации.

Момент максимального отклонения от положения равновесия, т.е. когда ; скорость маятника равна 0 и . В момент прохождения маятником положения равновесия ( ), тогда

Тогда по закону сохранения , откуда следует, что - это формула связи максимальной скорости с амплитудой колебаний.

Итак, полная энергия – есть величина постоянная и равна