
- •Теория автоматов Конспект лекций Уровни представления эвм.
- •Операционные элементы. (оэ)
- •Процессор гса:
- •Достоинства и недостатки.
- •Операционное устройство для выполнения операций алгебраического сложения двоичных чисел.
- •Суммирование при использовании прямого кодирования.
- •Суммирование чисел при использовании обратного кода.
- •Д ополнительный код.
- •Модифицированный код.
- •Пример суммирования.
- •Конечные автоматы.
- •Теория конечных автоматов
- •Способы задания функций переходов.
- •Автоматы ( с выходным преобразователем)
- •Способы задания автоматов
- •Способы задания автомата Миля
- •Преобразование автоматов из Миля в Мура и обратно Понятие эквивалентности автоматов
- •Преобразование Мура в Миля
- •Техника преобразований.
- •Обратный переход. Построение Мура для заданного Миля.
- •Частичные или не полностью определенные автоматы.
- •Синтез конечных автоматов.
- •Абстрактный синтез конечных автоматов.
- •Построение дерева входных последовательностей.
- •Структурный этап синтеза автоматов.
- •Основные этапы структурного синтеза.
- •Типы памяти.
- •Основные типы триггеров.
- •Пример структурного синтеза синхронного автомата.
- •`Временная диаграмма.
- •Этап минимизации автомата при абстрактном синтезе. Минимизация полностью определенного автомата.
- •Алгоритмы минимизации на основе треугольной матрицы.
- •Минимизация числа состояний частичного автомата.
- •Минимизация частичного автомата.
- •Абстрактный этап синтеза конечного автомат. (неканонический метод).
- •Алгоритм перехода от граф схемы микропрограммы к автомату Мура.
- •Учет взаимодействия операционного и управляющего автоматов. Алгоритм получения.
- •Алгоритм получения частичного автомата.
- •Множество входных значений.
- •Кодирование состояний синхронного автомата.
- •Кодирование соседними кодами.
- •Минимизация числа переключений элементов памяти.
- •Универсальный способ кодирования (для синхронного автомата).
- •Автомат с дешифратором.
- •Асинхронные автоматы.
- •Этапы синтеза асинхронного автомата.
- •Реализация асинхронного rs триггера на логических элементах.
- •Установочные входы в триггерах.
- •Синхронные элементы памяти.
- •Требования, предъявляемые к синхросигналу.
- •Синтез синхронного d триггера.
- •Синтез триггера с задержкой.Реализация асинхронного t триггера.
- •Исключение состязаний элементов памяти в синхронных автоматах.
- •Структура автоматов на плм и пзу.
- •Явление рисков в комбинационных узлах.
- •Исключение влияние рисков.
- •Построение схем без риска.
- •Алгоритм построения схемы без рисков по днф.
- •Алгоритм построения схемы без риска.
- •Автоматы, языки и грамматики.
- •Задача распознавания цепочек языка.
- •Классификация грамматик по Хомскому.
- •Примеры построения грамматик.
- •Грамматика для выполнения арифметических операций.
- •Соответствие конечных автоматов и автоматных грамматик.
- •Этапы для заданной автоматной грамматики.
- •Этапы для заданной автоматной грамматики.
- •Недетерминированные конечные автоматы.
- •Преобразование недетерминированного автомата в детерминированный.
- •Преобразование некоторых типов грамматики к автоматному ввиду.
- •Алгоритм получения правил, не содержащих правил вывода нетерминальных символов.
- •Построение распознавателей и преобразователей.
- •Построение распознавателей.
- •Алгоритм построения преобразователя.
Этапы синтеза асинхронного автомата.
Этап синтеза относится к асинхронному автомату также используется и в асинхронном, однако есть и отличие.
На этапе абстрактного синтеза нужно добавить следующие действия:
Осуществить перекодировку входных и выходных символов для обеспечения распознаваемости соседних одинаковых сигналов.
На этапе переходе от алфавитного оператора и автомату необходимо обеспечить все состояния автомата устойчивости.
Если уже автомат задан виде графа, то необходимо проверить устойчивость всех состояний, если это условие не обеспечивается , то надо вернуться в синтезе назад и обеспечить устойчивость, при этом может придется перекодировать входные символы.
Пример перекодирования входных и выходных символов:
P = {a,b} W = {a,b,c}

Вид входного сигнала:

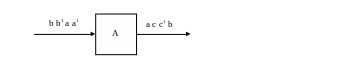
P1 = {a , a1 , b , b1} W = {a , b , c , c1}
На исходной временной диаграмме до перекодирования не различимы входные сигналы между I и II интервалом и III и IV . Выходной сигнал не различим между II и III интервалами.
На структурном этапе синтеза отличие следующие:
Иной тип элемента памяти, который используется в автомате.
Отличие в способе кодирования состояний автомата.
Иной метод синтеза комбинационного узла.
Кодирование состояний асинхронного автомата.
Цель кодирования – обеспечить устойчивую работу асинхронного автомата, затем устранение так называемого явления состязания памяти.
Состязание элементов памяти

τ1 = τ2 0110
τ1 > τ2 010010
τ1 < τ2 011110
Это явление называется состязанием элементов памяти.
Реальные элементы памяти обладают задержкой, величина задержки определяется не только в процессе изготовления, но и зависит от внешних факторов, поэтому заранее определить соотношение задержек различных элементов памяти не возможно.
Если в примере q1 и q2 имеют задержки τ1 и τ2 , то между ними могут быть соотношение, либо a либо b либо c, в этом случае переход из Si в Sj будет иметь варианты a,b,c. В случае b и c появляются дополнительные состояния 00 и 11, именно такие переходы через дополнительные состояния называются состязанием элементов памяти.
Состязания могут быть критическими и не критическими. Если состязание приводит к переходу в незапланированное устойчивое состояние, то такое состояние называется критическим.
Если же состязание приводит к переходу в незапланированное неустойчивое состояние, а потом и к переходу в верное устойчивое состояние, то такое состояние является некритическим.
Рассмотрим пример:
Закодируем в предыдущем графе 3 состояния следующим образом:
S/q |
q1 |
q1 |
S1 |
0 |
0 |
S2 |
0 |
1 |
S3 |
1 |
1 |
тогда автомат будет:
|
Pi / Si |
00 |
01 |
10 |
11 |
0 |
00 |
00 |
00 |
11 |
01 |
0 |
01 |
00 |
01 |
01 |
01 |
1 |
11 |
00 |
01 |
11 |
01 |

Рассмотрим 0011
q1q2
(τ1 τ2)
Пусть τ1 > τ2
10
0001- - >11
Состязание критическое, из-за задержки автомат оказывается в состоянии 01, для которого входной сигнал 10 является устойчивым или приводит к устойчивости, и переходит в состояние 11 не произойдет.
τ1 < τ2
10 10
00 10 11
Состязание не критическое.
Если промежуточное состояние в нашем случае некритическое состязание присутствует в графе, то состязание однозначно не критическое, однако если такого состояния нет, то на этапе кодирования можно считать его не критическим. После окончательного синтеза необходимо проверить на наличие петли в таком промежуточном состоянии.
2. Способы кодирования асинхронного автомата.
Так как заранее не известно соотношение между задержками элементов памяти, то необходимо кодировать так, чтобы избежать критических состояний элементов авмяти, либо избежать состязаний вообще.
Для того, чтобы избежать состязаний вообще необходимо закодировать состязания так, чтобы при новых переходах меняется только один элемент памяти.
Существует 2 способа кодирования:
Соседними кодами
Для того чтобы на каждом переходе не было состязаний, состояние между которыми есть переход колируют соседними кодами, которые отличаются только в одном разряде.
Однако число переходов обычно настолько велико, что используя код минимальной длины не удается на всех переходах закодировать состояние соседними кодами. В этом случае вводят дополнительное промежуточное состояние, которое является неустойчивым, такие состояния называются транзитивными. Число транзитивных состояний на любом переходе может быть любым. Они служат для задания определенного порядка изменения элементов памяти.

Кодирование унитарным кодом
При данном способе кодирования состояние Si кодируется кодом, в котором устанавливается 1 в I разряде.
Для отсутствия состязаний элементов памяти на каждом переходе из Si в Sj устанавливают транзитное состояние и кодируют его кодом, в котором 2 единицы в i и j разрядах.
Данный способ кодирования позволяет записать функции возбуждения прямо по графу, причем они будут не сложными.

Закодируем состояние из примера:
S1 = 100
S2 = 010
S3 = 001

D триггер (там где установка в 1)
D1 = ⌐X1⌐X2q3 v ⌐X1⌐X2q2 v q1⌐q2⌐q3
S3 S1/3 S2 S1/2 S1 S1
S1/3 S1 S12 S1 S1 S1/2
S1 S1/3
D2 = X1X2q1 v ⌐X1X2q3 v X1X2q3 v q1q2⌐q3
S1 S1/2 X2q3 X2q3 S2S2
S1/2 S2 S3 S23 S3 S23 S2 S12
S23 S2 S23 S2
D3 = X1⌐X2q1 v ⌐q1⌐q2q3
S1 S1/3 S3 S3
S13 S3
Нарисуем временную диаграмму:

Предположим, что автомат находится в состоянии S1 , q1,q2,q3 = 100, а входные сигналы X1 X2 = 01, функции возбуждения триггера дают следующие значения D1 = 1, D2 = 0, D3 = 0, что подтверждает состояние 100, до момента t0 схема устойчива.
Схема X1 в момент t0 изменяет D2, которое устанавливает к моменту t1 и вызывает изменение q2 к моменту времени t2; на интервале t2 и t3 получаем состояние 110, т.е. S12. Смена q2 сбрасывает D1 , которое в свою очередь переводит q1 в ноль (момент t4) , после t4 автомат находится в состоянии 010 , т.е. в состоянии S2.
При переходе из S1 в S2 последовательно меняется вначале q2 и затем q1. Это обеспечивало отсутствие состязаний элементов памяти, с другой стороны затянуло переход из S1 в S2, т.е. снизило быстродействие.
Запишем функции возбуждения для RS триггера.
В отличие от D триггера RS должны меняться, когда он сбрасывается и переходит в 1.
R = 1 – сброс
1 0
S = 1 – установка
0 1
R = 1
0 0
S = 1
1 1
S1 = q3⌐X1⌐X2 v q2⌐X1⌐X2
S3 S1/3(01) S2S1/2 (01)
S1/3 S1(11) S1/2 S1(11)
R1 = q2X1X2 v q3X1⌐X2
S1/2 S2(10) S1/3S3 (10)
S2 S2 (00) S2 S3(00)
S2 = q1X1X2 v q3X2
S1 S1/2(01) S3S2/3 (01)
S1/2 S2(11) S2/3 S2(11)
R2 = q2⌐X1⌐X2
S1/2 S1(10)
S1 S1 (00)
S3 = q1X1⌐X2 = q1⌐ q2⌐ q3X1⌐X2 v q1⌐q2q3X1⌐X2
S1 S1/3(01) (01)
S1/3 S3(11)
Два разряда q1q2 10 определяют 2 состояния S1 и S13 , один разряд q1 = 1 определяет 3 состояния S1,S13,S12, т.е. состояние S1 и транзитное от него. В записи для S3 присутствует также X1 , ⌐X2 , что однозначно удаляет состояние S12 следовательно, вместо q1⌐q2, можно записать только q1 и выражение q1X1⌐X2 будет определять только 2 состояния S1 S13.
R3 = q3⌐X1⌐X2 v q3X2
S3 S1(10) S2/3S2(10)
S1 S1(00) S2 S2(00)
Рассмотрим временную диаграмму S1S2
q1 |
q2 |
q3 |
X1 |
X2 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
|
Следовательно S3 = 0 , R3 = 0

Классификация по логическому функционированию делят на RS , JK , D , T.
По принципу записи и считыванию информации.
Триггеры делят:
В зависимости от наличия или отсутствия синхросигнала (синхронные и асинхронные)
В зависимости от времени записи новой информации и ее появление на выходе делят на триггеры с задержкой( с разделением процессов записи и считывания) и триггеры без задержки (без разделения) процессов записи и считывания.
В триггерах с задержкой новое значение появляется на выходе по окончанию сигнала, который произвел запись этого нового значения.
На примере RS триггера:
Асинхронный
без задержки

с задержкой
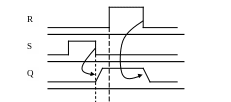

Синхронный
без задержки
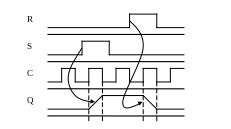
с задержкой

